آشنایی با آزمون نسبت تک نمونه‌ای

در این مقاله با آزمون نسبت تک نمونه‌ای (one proportion Z-test) آشنا می‌شویم. همچنین حدود اطمینان را نیز برای نسبت نمونه محاسبه می‌کنیم.

کاربرد آزمون نسبت تک نمونه‌ای

زمانی که ما یک نسبت از یک نمونه را با یک نسبت مفروض مقایسه می‌کنیم، می‌توانیم از آزمون نسبت تک نمونه‌ای یا آزمون نیکویی برازش کای اسکوئر استفاده کنیم.

توجه داشته باشید که اگر ما تفاوت بین دو نسبت را بررسی کنیم، می‌توانیم از آزمون دو نسبت یا آزمون کای اسکوئر استفاده کنیم که موضوع بحث این جلسه ما نیست. در جلسه دیگری آزمون دو نسبت را بررسی کرده‌ایم.

فرمول آزمون نسبت تک نمونه‌ای

فرمول آزمون نسبت تک نمونه‌ای را مشاهده می‌کنید.

مفهوم هر یک از اجزای فرمول به شرح زیر است:

آزمون نسبت زمانی استفاده می‌شود که نسبت موجود در یک نمونه را با نسبت مفروض در فرض صفر (H0) مقایسه می‌کنیم.

در حقیقت صورت کسر Z، تفاوت بین نسبت نمونه و نسبت مفروض را نشان می‌دهد. در حالی‌که مخرج کسر Z، خطای استاندارد نسبت نمونه را نشان می‌دهد.

مقایسه آزمون تی تک نمونه‌ای و آزمون نسبت تک نمونه‌ای

فرمول آزمون تی تک نمونه‌ای و آزمون نسبت تک نمونه‌ای را در ادامه آورده‌ام.

همانطور که ملاحظه می‌کنید، در صورت کسر آزمون تی تک نمونه‌ای تفاوت بین میانگین نمونه و مقدار پیش‌فرض قرار دارد. در حالی‌که در آزمون نسبت تک نمونه‌ای تفاوت بین نسبت نمونه و نسبت مفروض در صورت کسر قرار می‌گیرد. در مخرج کسر هر دو آزمون نیز خطای استاندارد قرار دارد.

مثال

در سال 2015 گروهی از دانشمندان نسبت رایج یک نوع آلرژی را در یک جمعیت بررسی کردند. مطالعه به این نتیجه رسید که 53 درصد از افراد این جمعیت دارای آلرژی بودند. در حالی که 47 درصد سالم و بدون آلرژی بودند.

پنج سال بعد، دانشمندان می‌خواستند بدانند که نسبت افراد مبتلا به آلرژی در جمعیت تغییر معنی‌دار یافته است یا خیر؟ اما در این زمان منابع کافی برای بررسی آلرژی تمام جمعیت وجود نداشت. به همین دلیل یک نمونه 100 فردی از جامعه گرفته شد. در این نمونه 49 فرد مبتلا به آلرژی و 51 فرد بدون آلرژی بودند (شکل 1).

شکل 1. نسبت افراد مبتلا به آلرژی در جمعیت اولیه و پنج سال بعد

آزمون فرضیات

برای بررسی تغییر معنی‌دار نسبت افراد مبتلا به آلرژی در جمعیت فعلی نسبت به جمعیت 5 سال قبل، ابتدا آزمون فرضیات را می‌نویسیم.

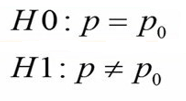
فرض صفر (H0) در این مثال گزاره‌ای است که بیان می‌کند نسبت افراد آلرژیک تغییری نکرده است. در حالی‌که فرض یک (H1) بیان می‌کند که در نسبت افراد آلرژیک تغییر معنی‌دار حاصل شده است.

توجه کنید که در آزمون فرضیات، P، نسبت جمعیت را در سال 2020 نشان می‌دهد. این نسبت در نمونه سال 2020، مقدار 49% بود. در حقیقت ما بر اساس نمونه مشاهده کردیم که نسبت افراد مبتلا به آلرژی در سال 2020 نسبت به سال 2015 کاهش یافته است. اما آیا این مقدار کاهش، تصادفی و ناشی از خطای نمونه‌گیری است یا واقعاً کاهش معنی‌دار رخ داده است؟ برای پاسخ به این سؤال از آزمون نسبت تک نمونه‌ای استفاده می‌کنیم.

محاسبات

مقادیر موجود برای جایگذاری در فرمول آزمون نسبت به شرح زیر است:

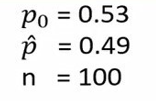
نسبت مربوط به فرض صفر (H0) ما 0.53 است. این همان نسبت افراد مبتلا به آلرژی در جمعیت اولیه است. در حقیقت این نسبت نسبت مفروض و شناخته شده ما است. نسبت فعلی افراد مبتلا به به آلرژی در جمعیت با پی-هت نشان داده می‌شود. حجم نمونه ما نیز 100 نفر است. الان می‌توانیم مقادیر را فرمول مربوط به آزمون نسبت تک نمونه‌ای وارد کنیم و مقدار Z را محاسبه کنیم.

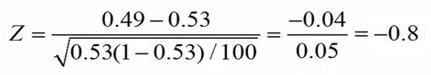
همانگونه که ملاحظه می‌کنید مقدار Z عدد 0.8- بدست آمد. الان ما می‌توانیم در توزیع Z استاندارد، احتمال مقادیر Z بالای 0.8 و کمتر از 0.8- را محاسبه کنیم. این مقدار همان P-value ماست.

شکل 2. نمایش مقدار P-value در توزیع Z استاندارد

در مثال ما مقدار P-value، عدد 0.42 بدست آمد. پس با توجه به این نتایج نمی‌توانیم فرض صفر (H0) را رد کنیم. پس شواهد کافی برای اینکه بگوییم نسبت افراد آلرژیک در جمعیت تغییر کرده است نداریم.

مفروضات آزمون نسبت تک نمونه‌ای

برای آزمون نسبت تک نمونه‌ای ما دو مفروض مهم در نظر می‌گیریم.

• نمونه ما شامل افراد مستقل کاملاً تصادفی از جمعیت باشد.
• توزیع آماره Z باید نرمال باشد.

مفروض اول که کاملا واضح است و نیازی به توضیح اضافی ندارد.

مفروض دوم دو حالت دارد که در ادامه بطور کامل توضیح می‌دهم.

نسبت فرض صفر نزدیک به 0.5

توزیع ما تحت فرض H0 مانند شکل 3 است. در جمعیت اولیه 53 درصد از افراد مبتلا به آلرژی و 47 درصد سالم هستند. زمانی که در آزمایش ما فقط دو نتیجه وجود داشته باشد، از درصد نتایج ما توزیعی به نام برنولی حاصل می‌شود که هیچ شباهتی با توزیع نرمال ندارد. اما چرا می‌گوییم که توزیع آماره Z باید نرمال باشد؟

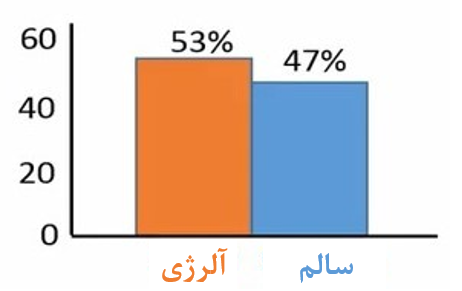
شکل 3. توزیع برنولی برای فرض H0

اگر یک نمونه به عنوان مثال 20 نفری از جمعیت اخذ کنیم، در این نمونه نسبتی از افراد انتخاب شده دارای آلرژی هستند. فرض کنید در نمونه اول که می‌گیریم 60 درصد افراد دارای آلرژی هستند (شکل 4).

شکل 4. نسبت افراد دارای آلرژی در نمونه 20 نفری

حالا فرض کنید مثلاً 10000 نمونه به این شکل از جمعیت بگیریم، در آنصورت 10000 نسبت نمونه‌ای خواهیم داشت. قطعاً هر بار که نمونه‌گیری می‌کنیم بر مبنای شانس نسبت افراد مبتلا به آلرژی در نمونه جدید با نمونه‌های قبلی مقداری متفاوت است.

اگر با استفاده از این 10000 نسبت یک هیستوگرام رسم کنیم، توزیعی مشابه با شکل 5 حاصل می‌شود.

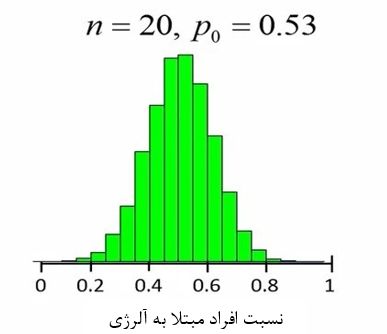
شکل 5. توزیع نسبت افراد دارای آلرژی

همانطور که در شکل 5 ملاحظه می‌کنید، اکثر نمونه‌های ما نسبتی نزدیک به 53 درصد دارند. پس انتظار داریم که 53 درصد از افراد ما در داخل جمعیت مبتلا به آلرژی باشند (شکل 6).

شکل 6. نمایش نسبت افراد مبتلا به آلرژی روی توزیع برنولی

نهایتاً اگر ما منحنی توزیع نرمال را بر هیستوگرام نسبت نمونه‌ها منطبق کنیم، می بینیم که نسبت نمونه ها تقریباً دارای توزیع نرمال است و مرکز این منحنی در موقعیت 0.53 قرار می‌گیرد. پس توزیع نرمال نسبت نمونه‌ها در این مثال صدق می‌کند.

نسبت فرض صفر نزدیک به 0 یا 1

حالا فرض کنید ما 10000 نمونه با حجم نمونه 20 از یک جمعیتی که 90 درصد آن مبتلا به آلرژی هستند تهیه کنیم (شکل 7).

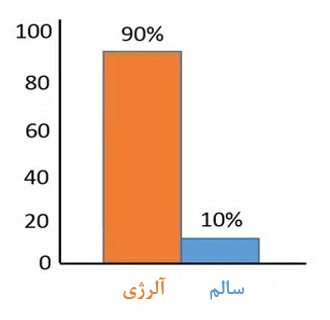
شکل 7. توزیع برنولی

اگر ما برای این مثال نیز توزیع نسبت افراد دارای آلرژی را رسم کنیم، توزیع بصورت شکل 8 خواهد بود.

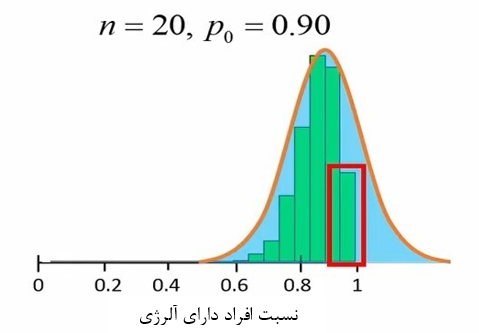
شکل 8. توزیع نسبت افراد دارای آلرژی

ستون های سبز نشان می‌دهد که توزیع این 10000 نمونه دیگر از توزیع نرمال تبعیت نمی‌کند. انحراف از توزیع نرمال به دلیل تجمع مقادیر در لبه توزیع نرمال رخ می‌دهد زیرا نسبت ها نمی توانند بیشتر از 100 درصد شوند.

اگر ما همین کار را با حجم نمونه 50 انجام دهیم، توزیعی بدست می‌آوریم که شکل آن به توزیع نرمال نزدیکتر است (شکل 9).

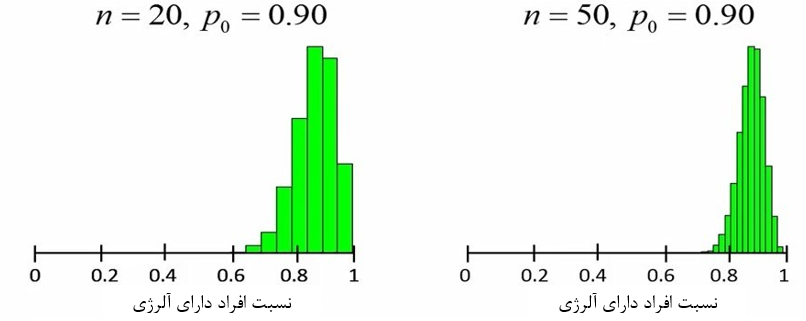
شکل 9. مقایسه توزیع نسبت‌ها در حجم‌های نمونه مختلف

بنابراین کمترین حجم نمونه ای که ما بتوانیم فرض کنیم که آماره Z توزیع نرمال دارد بستگی به نسبت مورد انتظار دارد. اگر نسبت مورد انتظار در فرض صفر نزدیک به صفر یا یک باشد باید حجم نمونه را افزایش دهیم تا بتوانیم مفروض نرمالیتی را در نظر بگیریم.

یک قانون سر انگشتی برای تعیین حجم نمونه با توجه به نسبت فرض H0 قانون زیر است.

این قانون بیان می‌کند که وقتی نسبت نمونه را در حجم نمونه ضرب می‌کنیم، حداقل باید عدد 5 بدست آید. در این صورت حجم نمونه متناسب با نسبت نمونه انتخاب می‌شود و می‌توانیم توزیع نرمال را برای نسبت‌ها در نظر بگیریم.

همانطور که می‌بینید ما با حجم نمونه 50، حداقل عدد 5 را داریم. پس اگر حجم نمونه ما 50 و نسبت فرض صفر (H0) 0.9 باشد، می‌توانیم مفروض نرمالیتی را در نظر بگیریم.

حدود اطمینان 95 درصد برای آزمون نسبت تک نمونه‌ای

برای آشنایی دقیق با مفهوم حدود اطمینان و نحوه تفسیر آن  آن به جلسه مربوطه مراجعه کنید.

فرمول حدود اطمینان 95 درصد برای آزمون نسبت تک نمونه‌ای به شرح زیر است:

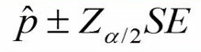
در جلسه مربوط به حدود اطمینان دیدیم که محدوده بین 1.96- تا 1.96+ در توزیع نرمال استاندارد، 95 درصد از محدوده توزیع Z را پوشش می‌دهد. پس مقدار Z را  1.96 در نظر می‌گیریم.

خطای استاندارد (SE) در فرمول حدود اطمینان دقیقاً از عبارت موجود در مخرج کسر Z استخراج می‌شود.

در این مثال، محاسبه خطای استاندارد بصورت زیر انجام می‌شود:

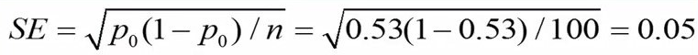
در این مثال خطای استاندارد را عدد 0.5 بدست آورده‌ایم.

الان می‌توانیم مقادیر مربوطه را در فرمول حدود اطمینان قرار دهیم و حدود اطمینان را محاسبه کنیم.

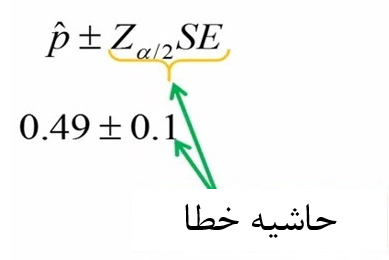
توجه کنید که از ضرب مقدار Z در SE حاشیه خطا بدست می‌آید. حاشیه خطا نشان می‌دهد نسبت واقعی جمعیت در چه بازه‌ای قرار دارد. در این مثال، حاشیه خطا را 10 درصد بدست آورده‌ایم.

بنابراین حدود اطمینان 95 درصد، در بازه 0.39 تا 0.59 قرار گرفت. پس ما 95 درصد اطمینان داریم که نسبت واقعی افراد مبتلا به آلرژی در سال 2020، در بازه 0.39 و 0.59 قرار دارد.

چون این محدوده شامل مقدار مفروض 0.53 می‌شود، پس نمی‌توانیم فرض H0 را رد کنیم. چرا که مقدار 0.53 یک مقدار منطقی برای محدوده 0.39 تا 0.59 به شمار می‌رود. نهایتاً نتیجه می‌گیریم که نسبت افراد مبتلا به آلرژی در جمعیت تغییری نکرده است.

توجه کنید که این حدود اطمینان، بازه‌ای عریض است که نااطمینانی یا عدم قطعیت در مورد نسبت افراد دارای آلرژی در جمعیت ایجاد می‌کند. برای کاهش بازه حدود اطمینان باید حجم نمونه را افزایش دهیم.