آشنایی با آزمون فرضیات

در این مقاله در مورد آزمون فرضیات (Hypothesis testing) صحبت می‌کنیم و این مبحث را بطور کامل با مثال شرح می‌دهیم.

قبل از مطالعه این مقاله، حتماً مطالب مربوط به حدود اطمینان و  آزمون‌های تی نمونه‌ای، تی مستقل و  تی زوجی را ببینید.

تعریف فرضیه و مفهوم آن

فرضیه گزاره‌ای است که می‌تواند مورد آزمون قرار گیرد. این گزاره می‌تواند صحیح یا غلط باشد. مثلاً به چند فرضیه زیر دقت کنید.

• داروی a در کاهش حجم تومور بهتر از داروی b عمل می‌کند.
• گیاهان مزرعه a بلندتر از گیاهان مزرعه b هستند.
• افراد مسن فشار خون بالاتری نسبت به افراد جوان دارند.
• میانگین دمای هوا در تیرماه نسبت به شهریورماه بیشتر است.

در آزمون فرضیات آماری هدف ما آزمون فرضیه صفر (H0) در برابر فرضیه مقابل (H1) است.

فرضیه صفر (H0) گزاره‌ای است که در مقابل فرضیه یک H1 قرار دارد.

در حقیقت فرضیه صفر نشان از عدم وجود رابطه، عدم وجود تفاوت یا هر اتفاقی است که نشان دهد همه چیز نرمال است.

در برابر فرضیه صفر، فرضیه مقابل (H1) قرار دارد. این فرضیه نشان از وجود اختلاف یا ارتباط است.

توجه کنید که فرضیه صفر را با اچ صفر (H0) و فرضیه یک را با اچ 1 (H1) نشان می دهیم.

آزمون فرضیات آماری

برای انجام آزمون فرضیات آماری 5 گام زیر را باید انجام دهیم

• گام اول: مشخص کردن فرض صفر (H0) و یک (H1)
• گام دوم: انتخاب یک سطح معنی‌دار (آلفا) برای آزمون
• گام سوم: اجرای آزمایش و انتخاب یک آزمون آماری مناسب
• گام چهارم: محاسبه مقدار P-value
• گام پنجم: مقایسه مقدار P-value با سطح معنی‌دار (آلفا) برای تصمیم‌گیری در مورد رد یا رد نکردن فرضیه

مثال برای آزمون فرضیات

فرض کنید می‌خواهیم آزمون کنیم که آیا بین ارتفاع گیاهان موجود در مزرعه A و B تفاوت معنی‌دار وجود دارد یا خیر؟ برای این کار گام‌های مربوط به آزمون فرضیات را گام به گام انجام می‌دهیم.

شکل 1. مقایسه مزرعه A و B از نظر ارتفاع گیاه

گام اول: مشخص کردن فرض صفر (H0) و یک (H1)

فرضیات H0 و H1 را به این صورت مطرح می‌کنیم.

مفهوم هر یک از فرضیات به شرح زیر است:

H0: بین میانگین ارتفاع گیاهان مزرعه A و B تفاوت وجود ندارد.

H1: بین میانگین ارتفاع گیاهان مزرعه A و B وجود دارد.

توجه داشته باشید که ما از حرف یونانی مو برای میانگین جمعیت استفاده می‌کنیم. علامت مساوی (=) نشان می‌دهد که ما در مورد تساوی میانگین ارتفاع بوته جمعیت A و جمعیت B صحبت می‌کنیم.

گام دوم: انتخاب یک سطح معنی‌دار (آلفا) برای آزمون

این گام خیلی ساده است. فقط باید در مورد سطح معنی‌دار (آلفا) آزمون تصمیم بگیریم. محققان عموماً برای سطح معنی‌دار، سطح پنج یا یک درصد را انتخاب می‌کنند.

در آمار اغلب تمایل داریم به هر قضاوتی که انجام می‌دهیم حداقل 95 درصد اطمینان داشته باشیم. این موضوع به این معنی است که مقدار آلفا حداقل پنج درصد در نظر گرفته می‌شود. با وجود این، هر محقق می‌تواند، هر مقداری را برای آلفا اتخاذ کند.

گام سوم: اجرای آزمایش و انتخاب یک آزمون آماری مناسب

در گام سوم داده‌ها جمع‌آوری می‌شود. یعنی نمونه‌ای از هر مزرعه اخذ و ارتفاع گیاهان در آن نمونه اندازه‌گیری می‌شود. به عنوان مثال میانگین ارتفاع گیاهان در مزرعه A، 4.5 و میانگین ارتفاع گیاهان در مزرعه B، 5 حاصل شده است (شکل 2).

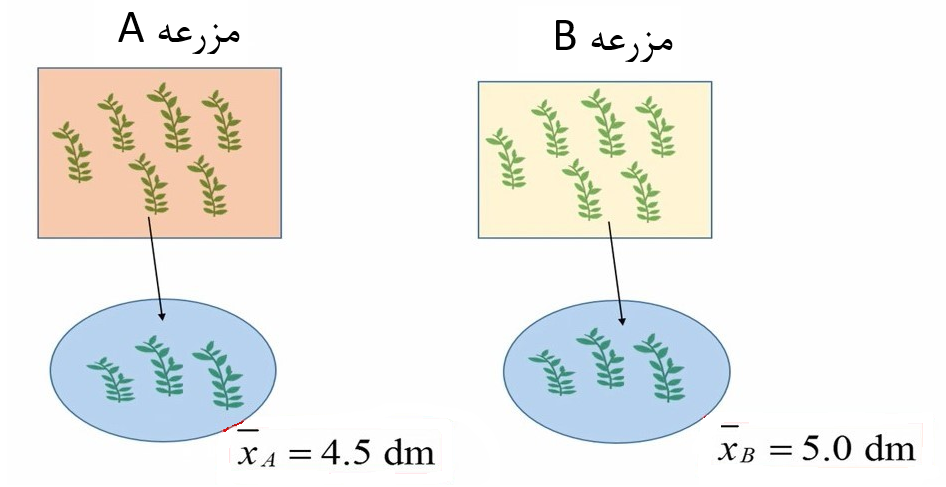
شکل 2. میانگین ارتفاع گیاه در مزرعه A و B

الان باید آزمون آماری مناسبی برای مقایسه میانگین ارتفاع گیاهان دو مزرعه انتخاب کنیم. برای این مثال، آزمون آماری تی مستقل مناسب است.

گام چهارم: محاسبه مقدار P-value

در این گام باید مقدار P-value را محاسبه کنیم. مقدار P-value اغلب با استفاده از یک نرم افزار آماری محاسبه می‌شود.

گام پنجم: مقایسه مقدار P-value با سطح معنی‌دار (آلفا)

در این بخش مقدار P-value محاسبه شده را با سطح معنی‌دار انتخاب شده در گام دوم مقایسه می‌کنیم. اگر مقدار P-value از مقدار آلفا کوچکتر باشد، می‌توانیم فرضیه صفر را رد کنیم. اما اگر مقدار P-value بزرگتر از مقدار آلفا باشد نمی‌توانیم فرض صفر را رد کنیم.

توجه بسیار مهم این است که مقدار آلفا قبل از انجام آزمایش تعیین می‌شود و اغلب عدد 0.05 انتخاب می شود. اما مقدار P-value می‌تواند عددی بین صفر و یک باشد.

برای هر آزمایش دو حالت وجود دارد:

حالتی از آزمون فرضیات که در آن فرض H0 رد می‌شود:

برای مثال، اگر مقدار P-value در گام چهارم، 0.02 بدست بیاید چون این مقدار کوچکتر از مقدار آلفا یعنی 0.05 است، ما فرضیه صفر (H0) را رد می‌کنیم و نتیجه می‌گیریم که بین میانگین ارتفاع گیاهان مزرعه A و B تفاوت معنی‌دار وجود دارد. توجه کنید که فرضیه مقابل (H1)، وجود تفاوت بین میانگین ارتفاع مزرعه A و B را نشان می‌دهد.

از آنجایی که ما نمونه‌هایمان را از جمعیت انتخاب کرده‌ایم، هرگز نمی‌توانیم به هر یک از فرضیه‌ها 100 درصد اطمینان کنیم و همیشه به میزان آلفا، احتمال خطا در قضاوتمان وجود دارد. چون ما هرگز تمام گیاهان موجود در دو مزرعه را اندازه گیری نکرده‌ایم.

زمانی که فرض H0 را رد می‌کنیم اینطور بیان می‌کنیم که تفاوت معنی‌دار بین میانگین ارتفاع گیاهان مزرعه A و B وجود دارد. این موضوع به این معنی‌ است که شواهد قوی وجود دارد که میانگین ارتفاع گیاهان در مزرعه A با مزرعه B متفاوت است.

حالتی از آزمون فرضیات که در آن فرض H0 رد نمی‌شود:

حالا فرض کنید مقدار P-value در آزمون آماری ما 0.45 بدست آمده است. از آنجا که این مقدار، بزرگتر از مقدار آلفا است، فرضیه صفر را رد نمی‌کنیم. بنابراین نتیجه می‌گیریم که میانگین ارتفاع گیاهان بین مزرعه A و B تفاوت ندارد. بنابراین در اینصورت شواهد قوی برای رد فرض H0 نداریم.

آزمون فرضیات یکطرفه و دو طرفه

در مثال مذکور، ما از گزاره‌های دو طرفه استفاده کردیم. به این معنی که ما تفاوت بین میانگین ارتفاع گیاهان را در دو جمعیت آزمون کردیم. اما ما می‌توانیم آزمون فرضیات یکطرفه را نیز به شرح زیر مطرح کنیم.

اگر فرضیه H1 را به شرح زیر بنویسیم فرضیه یکطرفه خواهیم داشت.

• میانگین ارتفاع گیاهان در جمعیت A بزرگتر از میانگین ارتفاع گیاهان در جمعیت B است. یا برعکس میانگین ارتفاع گیاهان در مزرعه A کوتاه‌تر از میانگین ارتفاع گیاهان در جمعیت B است.

البته بهترین نوع فرضیه باید بر مبنای نوع مطالعه مشخص شود. اما فرضیات دو طرفه معمولتر از فرضیات یکطرفه هستند. چرا که ما عموماً هیچ دیدگاهی نسبت به جمعیت اولیه و بزرگتر یا کوچکتر بودن میانگین‌ها نسبت به هم نداریم.

نکته مهم در این باره این است که ما باید قبل از انجام آزمایش، یکطرفه یا دوطرفه بودن فرضیات خودمان را مشخص کنیم.