آشنایی با آزمون تی مستقل

در این مقاله آزمون تی مستقل (Independent sample t-test) را با مثال بررسی می‌کنیم.

آزمون‌های تی (t) زمانی استفاده می‌شوند که آماره ما از توزیع تی تبعیت می‌کند. این آزمون‌ها سه نوع هستند:

• آزمون تی تک نمونه‌ای
• آزمون تی مستقل
• آزمون تی زوجی

دو آزمون تی تک نمونه‌ای و تی زوجی را در مقالات دیگری بررسی کرده‌ایم.

کاربرد آزمون تی مستقل

آزمون تی مستقل یا تی نمونه‌های جفت نشده (Unpaired t-test) آزمون آماری است که میانگین دو جمعیت را مقایسه می‌کند. عموماً ما نمی‌توانیم متغیر مورد نظرمان را در کل افراد جمعیت اندازه‌گیری کنیم. پس ابتدا از جمعیت نمونه‌گیری می‌کنیم و بعد با استفاده از آزمون تی مستقل بررسی می‌کنیم که آیا میانگین دو جمعیت تفاوت دارند یا خیر؟

نکته مهمی که وجود دارد این است که اگر مقدار واریانس دو جمعیت برای ما شناخته شده باشد، آزمون Z به آزمون t ترجیح داده می‌شود.

مثال آزمون تی مستقل

فرض کنید می‌خواهیم بدانیم که بین فشار خون افراد 35-20 ساله و فشار خون افراد 55-36 ساله تفاوت وجود دارد یا خیر؟ به این منظور چهار فرد را بطور تصادفی از جمعیت اول و چهار فرد دیگر را بطور تصادفی از جمعیت دوم انتخاب می‌کنیم. توجه کنید که اگر مطالعه ما واقعی بود، باید تعداد افراد بیشتری را برای مطالعه مان انتخاب می کردیم. تنها دلیلی که ما چهار نفر را انتخاب کردیم، ساده سازی مطلب است. چون در این مثال افراد دو گروه کاملاً از هم مستقل هستند و هیچ ارتباطی با هم ندارند، برای حل این مسئله از آزمون تی مستقل استفاده می‌کنیم.

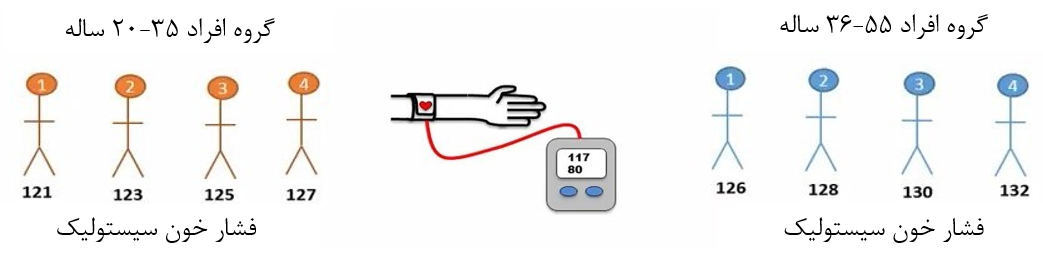
شکل 1. تشکیل دو گروه افراد و اندازه‌گیری میزان فشار خون افراد

مطرح کردن فرضیات

نحوه دقیق مطرح کردن فرضیات تحقیق و مفهوم دقیق آن را قبلاً در طی یک مقاله بررسی کرده‌ایم.

ابتدا فرضیات تحقیق را به شکل زیر مطرح می‌کنیم:

فرض صفر (H0): گزاره‌ای است که بیان می‌کند میانگین فشار خون سیستولیک دو جمعیت با هم برابر است.

فرض یک (H1): گزاره‌ای است که بیان می‌کند میانگین فشار خون سیستولیک بین دو گروه متفاوت است.

آزمون تی مستقل به ما کمک می‌کند که در مورد فرضیات تصمیم بگیریم.

تعیین سطح معنی‌دار آزمون (آلفا)

قدم دوم مشخص کردن سطح معنی‌دار آزمون است. در این مثال ما سطح معنی‌دار را پنج درصد در نظر می‌گیریم.

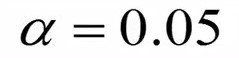
انجام آزمایش

در این مثال، پس از انجام آزمایش، میانگین فشار خون افراد جوان 35-20 ساله 124 و میانگین فشار خون افراد میان سال 55-36 ساله 129 بدست آمد. مطابق شکل 2، میانگین فشار خون سیستولیک در افراد میان‌سال بیشتر از افراد جوان بدست آمد (شکل 2).

شکل 2. نمایش میانگین فشار خون در دو گروه سنی

اختلاف فشار خون در دو گروه می‌تواند ناشی از انتخاب تصادفی افراد در هر گروه باشد. به این معنی که ممکن است بطور تصادفی از افراد جوان نمونه‌هایی انتخاب شود که فشار خون پائین دارند یا بطور تصادفی از افراد میان‌سال نمونه هایی انتخاب شود که فشار خون بالا دارند. آزمون تی مستقل به ما کمک می‌کند که متوجه شویم آیا تفاوت مشاهده شده بین میانگین نمونه‌ها تصادفی است یا واقعاً بین دو گروه تفاوت معنی‌دار وجود دارد؟

محاسبه مقدار تی

فرمول محاسبه آماره تی برای آزمون تی مستقل زمانی که حجم نمونه‌ها با هم برابر باشد به این شرح است:

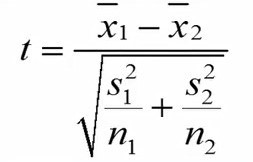
چون ما برای هر گروه چهار مشاهده داریم، دو گروه ما حجم نمونه یکسانی دارد.

در این فرمول ایکس-بار، نشان دهنده میانگین است. s² نشان دهنده واریانس و n حجم نمونه را نشان می‌دهد.

تفاوت میانگین فشار خون دو گروه در صورت کسر آزمون تی قرار دارد. در مخرج کسر هم خطای استاندارد تفاوت‌ها قرار دارد. قبلاً در طی مطالب جداگانه‌ای نحوه محاسبه میانگین، واریانس و خطای استاندارد را بررسی کرده‌ایم.

با جایگذاری موارد در فرمول آزمون تی، مقدار تی 2.74- بدست می‌آید.

بعد از محاسبه مقدار تی، باید به توزیع تی با درجه آزادی 6 مراجعه کنیم. چون در این آزمایش، ما دو میانگین را تخمین می‌زنیم، از درجه آزادی n1+n2-2 استفاده می‌کنیم (شکل 3). قبلاً مفهوم درجه آزادی و مشخص کردن آن را در جلسه جداگانه‌ای بررسی کرده‌ایم.

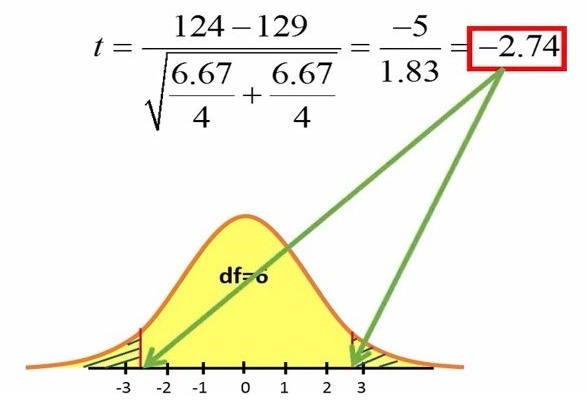
شکل 3. مشخص کردن مقادیر تی روی توزیع تی

حالا می‌توانیم از یک نرم افزار برای محاسبه ناحیه سمت چپ 2.74- و ناحیه سمت راست 2.74+ استفاده کنیم. این نواحی به ما مقدار P-value را می‌دهد (شکل 4). در این مثال مقدار P-value عدد 0.034 بدست آمد.

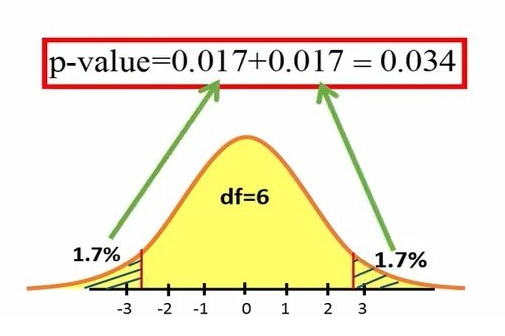
شکل 4. محاسبه مقدار P-value

تفسیر P-value

مقدار P-value را به این صورت می‌توانیم تفسیر کنیم که اگر فرض صفر (H0) ما صحیح باشد، یعنی گزاره‌ای که دو میانگین را مساوی فرض می‌کند، صحیح باشد، احتمال مشاهده آماره تی 2.74 یا بیشتر ، یا 2.74- و کمتر برابر با 3.4 درصد است. بنابراین احتمال اینکه آماره تی محاسبه‌ شده ما در این ناحیه قرار گیرد، بسیار کم است.

پس چون مقدار P-value در این مثال کمتر از 0.05 است، می‌توانیم فرض صفر را رد کنیم. همچنین به دلیل اینکه میانگین فشار خون در افراد میان‌سال نسبت به افراد جوان بیشتر است، می‌توانیم نتیجه بگیریم که افراد محدوده سنی 55-36 سال بطور متوسط فشار خون بالاتری نسبت به افراد محدوده سنی 35-20 سال دارند.

حدود اطمینان 95 درصد برای آزمون تی مستقل

نتایج آزمون تی مستقل عموماً با 95 درصد اطمینان گزارش می‌شود. فرمول محاسبه حدود اطمینان تفاوت میانگین‌ها بصورت زیر است.

کافی است در فرمول حدود اطمینان، تفاوت میانگین‌ها و خطای استاندارد را جایگذاری کنیم تا حدود اطمینان بدست آید. مقدار تی با درجه آزادی n1+n2-2 و سطح معنی‌داری 0.025 را از جدول توزیع تی می‌توانیم استخراج کنیم.

با جایگذاری کمیت‌های مربوطه در فرمول محدوده اطمینان میانگین جمعیت 9.5- تا 0.5- بدست آمد.

تفسیر حدود اطمینان 95 درصد

بر مبنای حدود اطمینان بدست آمده می‌توانیم بگوییم که 95 درصد مطمئن هستیم که تفاوت واقعی بین میانگین جمعیت‌ها در محدوده 9.5- تا 0.5- قرار می‌گیرد. چون محدوده اطمینان مقدار صفر را در بر نمی‌گیرد، می‌توانیم فرض صفر را بر مبنای آن رد کنیم.

مفروضات آزمون تی مستقل

برای انجام آزمون تی مستقل دو مفروض اصلی وجود دارد.

• توزیع نرمال مشاهدات در هر گروه
• تساوی واریانس‌ها

بررسی نرمالیتی دو گروه

اگر توزیع داده‌های ما در هر گروه تقریباً نرمال باشد، می‌توانیم فرضیه نرمالیتی را تأیید نماییم. به عنوان مثال به شکل 5 دقت کنید مقادیر دو گروه در شکل 5 تقریباً توزیع نرمال دارند و برای این مقادیر هیچ مشاهده پرتی در مشاهده نمی‌شود.

شکل 5. بررسی نرمالیتی داده‌ها در هر گروه

اما اگر چولگی مقادیر، زیاد باشد، نمی‌توانیم مفروض نرمالیتی را برای داده‌ها در نظر بگیریم. مثلاً به داده‌های شکل 6 دقت کنید که در آن چولگی شدید در داده‌ها وجود دارد. همچنین چند داده‌ پرت نیز در بین داده‌ها دیده می‌شود.

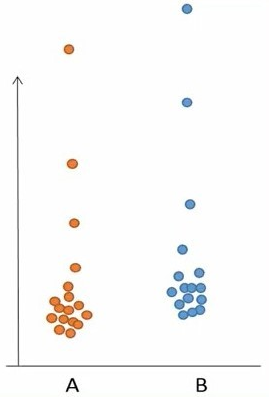
شکل 6. چولگی داده‌ها در گروه‌ها

اگر از مقاله قضیه حد مرکزی به یاد داشته باشید، گفتیم که اگر حجم نمونه ما بزرگتر از 30 باشد، می توانیم فرض کنیم که میانگین نمونه‌ها توزیع نرمال دارد. در این صورت آزمون تی مستقل ما هنوز معتبر است. مگر اینکه داده‌های پرت یا چولگی شدید داشته باشیم. اگر در حدود 15 داده در هر گروه داشته باشیم و مقادیر ما چولگی شدید داشته باشد، باید از آزمون های ناپارامتری استفاده کنیم.

نحوه بررسی داده‌ها از نظر نرمالیتی

بطور کلی بررسی نرمالیتی داده‌ها را می‌توانیم از طریق دو روش انجام دهیم.

• روش‌های گرافیکی
• آزمون‌های نرمالیتی مانند شاپیرو-ویلک یا کولموگروف-اسمیرنوف

تساوی واریانس‌ها

مفروض دوم برای آزمون تی مستقل تساوی واریانس‌هاست. همانطور که در شکل 7 ملاحظه می‌کنید واریانس نمونه اول 25 و واریانس نمونه دوم 19 است. آیا بین دو واریانس اختلاف معنی‌دار آماری وجود دارد؟

شکل 7. بررسی تساوی واریانس‌ها در دو گروه

برای مقایسه تساوی واریانس‌های دو گروه از آزمون لون (Levene’s test) استفاده می‌کنیم. ابتدا آزمون فرضیات تساوی واریانس‌ها را مطرح می‌کنیم. فرض صفر H0 و یک H1 را برای بررسی تساوی واریانس‌ها بصورت زیر می‌نویسیم.

H0: تساوی واریانس‌ها

H1: نبود تساوی واریانس‌ها

اگر در آزمون لون مقدار P-value کوچکتر از 0.05 شود، می‌توانیم فرض صفر را در سطح خطای 5 درصد رد کنیم و بگوییم که واریانس‌ها تساوی ندارند. اگر دو گروه واریانس مساوی نداشتند می‌توانیم به جای آزمون تی مستقل از آزمون ولش (Welch’s t-test) استفاده کنیم. این آزمون عدم تساوی واریانس‌های دو گروه را کنترل می‌کند.