آشنایی با خطای استاندارد میانگین

در این مقاله مفهوم خطای استاندارد میانگین (Standard error of the mean) را یاد می‌گیریم و تفاوت آن را با انحراف استاندارد بررسی می‌کنیم.

قبل از مشاهده این قسمت باید با مفهوم میانگین و انحراف استاندارد آشنا باشید. برای آشنایی به مقالات مربوطه مراجعه نمایید.

خطای استاندارد میانگین با استفاده از فرمول زیر محاسبه می‌شود.

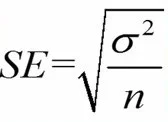
در این فرمول سیکما نشان دهنده انحراف استاندارد و n حجم نمونه را نشان می‌دهد.

مثال خطای استاندارد میانگین

فرض کنید قد تمام افراد یک جامعه 10000 نفری را اندازه‌گیری کرده‌ایم. میانگین قد 170 و انحراف استاندارد 10 بدست آمده است. شکل 1 هیستوگرام داده‌ها را نشان می‌دهد.

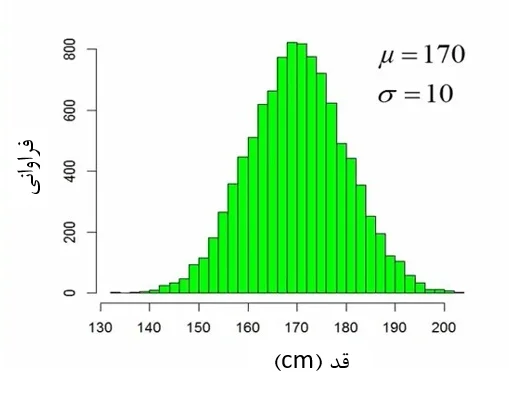
شکل 1. هیستوگرام قد افراد

حالا فرض کنید یک نمونه شامل 4 نفری از این جامعه می‌گیریم. میانگین این نمونه بطور تصادفی 166 بدست می‌آید (شکل 2).

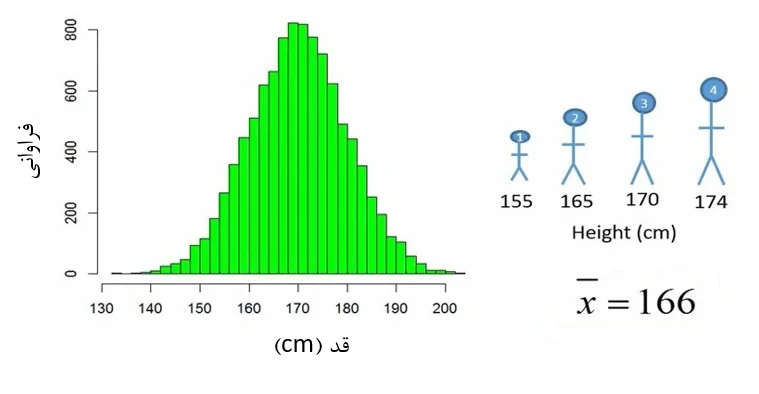
شکل 2. اخذ نمونه چهار نفری از جامعه و محاسبه میانگین

اگر به همین ترتیب نمونه‌های متعددی از این جامعه بگیریم و میانگین این نمونه‌ها را محاسبه کنیم. جامعه دیگری به نام جامعه میانگین نمونه‌ها خواهیم داشت. فرض کنید مثلاً 10000 بار از این جامعه نمونه‌های 4 نفری اخذ می‌کنیم. در این صورت 10000 میانگین خواهیم داشت (شکل 3). توجه کنید که در هر بار نمونه‌گیری افراد متفاوتی در نمونه‌های ما حضور دارند. بنابراین میانگین‌های ما مقداری تفاوت خواهند داشت.

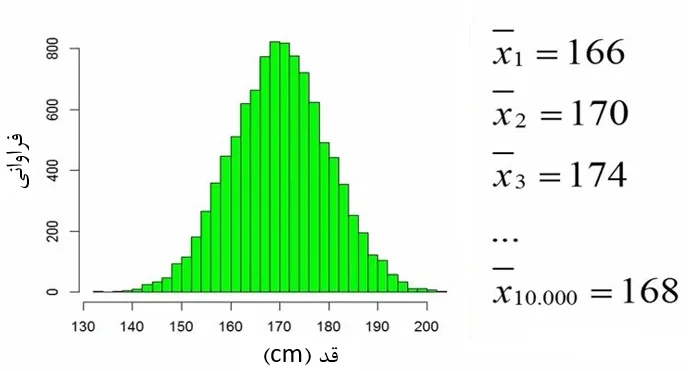
شکل 3. اخذ 10000 نمونه چهار نفری و محاسبه میانگین

تشکیل جامعه نمونه‌ها

اگر برای 10000 نمونه هیستوگرام رسم کنیم، مشاهده می‌کنیم که توزیع مقادیر میانگین شکلی شبیه به توزیع نرمال دارد. قبلاً این مطلب را در قالب قضیه حد مرکزی بیان کرده‌ایم. توزیع جمعیت و توزیع نمونه‌ها در شکل 4 زیر قابل مشاهده است.

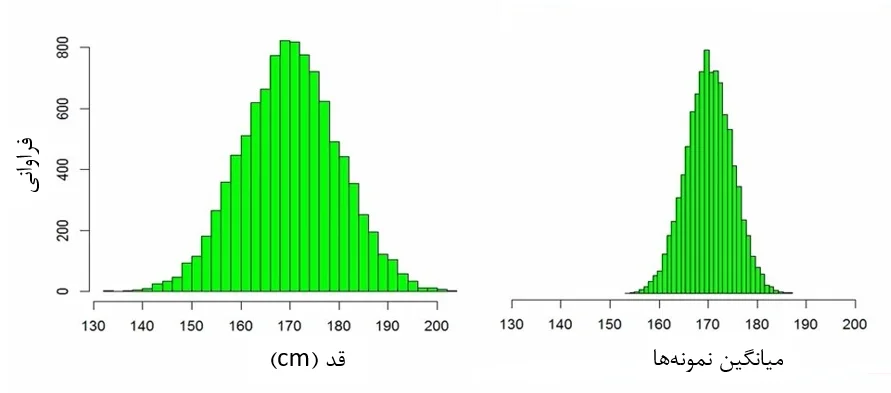
شکل 4. تشکیل جامعه نمونه‌ها

نکته مهم در این رابطه این است که اگرچه مقادیر میانگین محدوده‌ای بین 130 تا 210 دارند، توزیع میانگین نمونه‌ها محدوده‌ای بین 153 تا 187 است. اما چرا پراکندگی جامعه نمونه‌ها کمتر از جامعه اصلی است؟

به دلیل اینکه افراد بسیار کمی در جمعیت وجود دارند که قد خیلی کوتاه یا خیلی بلند داشته باشند، احتمال بسیار کمی وجود دارد که مثلاً 4 فرد بسیار قد کوتاه یا بسیار قد بلند بصورت تصادفی از جمعیت انتخاب شود. به همین خاطر هیچیک از میانگین‌ها خیلی کوچک یا خیلی بزرگ نیست. بنابراین انحراف استاندارد توزیع میانگین‌ها کمتر از انحراف استاندارد جمعیت اصلی است.

محاسبه انحراف استاندارد جامعه میانگین نمونه‌ها

در این بخش خطای استاندارد میانگین نمونه‌ها را محاسبه می‌کنیم. اگر انحراف استاندارد جامعه اصلی 10 و حجم نمونه‌های ما 4 باشد، می‌توانیم با استفاده از فرمول شکل 5، خطای استاندارد میانگین‌ها را محاسبه کنیم. توجه کنید که ما می‌توانیم بدون نمونه‌ گیری های متعدد از جامعه اصلی و با استفاده از انحراف استاندارد جامعه اصلی، انحراف استاندارد جامعه نمونه‌ها را محاسبه کنیم. کافی است انحراف استاندارد جامعه اصلی را تقسیم بر ریشه دوم حجم نمونه کنیم تا انحراف استاندارد جامعه نمونه‌ها بدست آید.

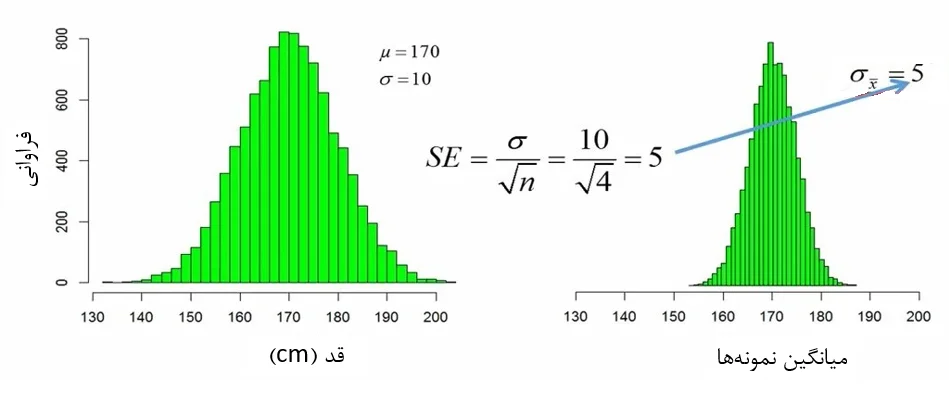
شکل 5. محاسبه خطای استاندارد

پس، خطای استاندارد دقیقاً تخمینی از انحراف استاندارد توزیع میانگین‌ نمونه‌هاست. بنابراین اگر ما انحراف استاندارد میانگین 10000 نمونه را از جمعیت مورد بررسی در مثال مذکور محاسبه کنیم، انتظار داریم که مقدار 5 بدست آید.

بنابراین انتظار داریم که تقریباً 68 درصد از میانگین نمونه‌های ما بین 165 تا 175 باشد. چون این فاصله به اندازه یک انحراف استاندارد از توزیع میانگین توزیع نمونه‌ها است.

نکته مهم در مورد خطای استاندارد میانگین

بار دیگر به فرمول خطای استاندارد دقت کنید.

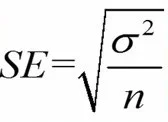
از فرمول خطای استاندارد مشخص است که وقتی حجم نمونه (n) افزایش می‌یابد، خطای استاندارد کم می‌شود. پس زمانی که حجم نمونه‌های ما زیاد شود، توزیع میانگین نمونه‌های ما باریک‌تر می‌شود.

فرض کنید ما مجدداً نمونه‌گیری را انجام دهیم. اما این بار به جای 4 فرد، 25 فرد از جامعه را انتخاب کنیم و میانگین آن‌ها را محاسبه کنیم (شکل 6).

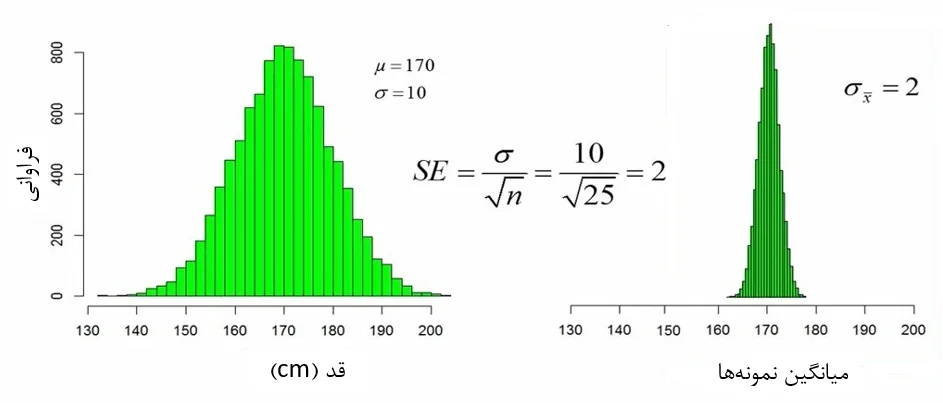
شکل 6. محاسبه خطای استاندارد با نمونه‌های 25 تایی

همانطور که ملاحظه می‌کنید، وقتی اندازه نمونه از 4 به 25 افزایش می‌یابد خطای استاندارد میانگین از 5 به 2 کاهش می یابد. پس اگر از همین جمعیت، 10000 نمونه 25 تایی بگیریم و هیستوگرام میانگین آن‌ها را رسم کنیم شکلی مانند شکل 6 حاصل می‌شود. توجه کنید که پراکندگی توزیع میانگین‌ها نمونه‌ها نسبت به حالتی که حجم نمونه‌ها 4 نفری بود کم می‌شود و توزیع باریکتر خواهد بود.

مقایسه انحراف استاندارد و خطای استاندارد میانگین

ما می‌توانیم کل داده‌های مثال قبل را مانند شکل 7 نشان دهیم.

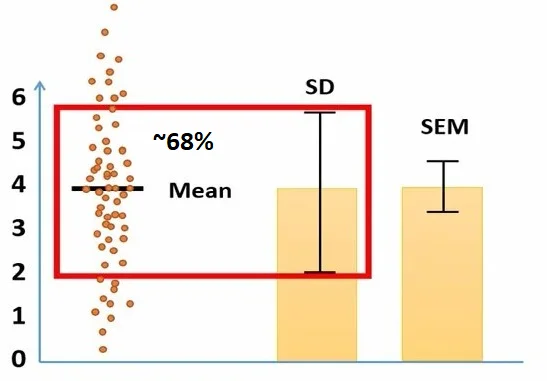
شکل 7. میانگین، انحراف استاندارد و خطای استاندارد

در شکل 7 ارتفاع ستون‌ها نشان دهنده میانگین است. انحراف استاندارد (SD) در این شکل در مورد پراکندگی داده‌ها در اطراف میانگین صحبت می‌کند. انحراف استاندارد را می‌توانیم اینطور تفسیر کنیم که 68 درصد از نقاط داده‌ها به فاصله یک انحراف استاندارد از میانگین قرار می‌گیرند (شکل 7).

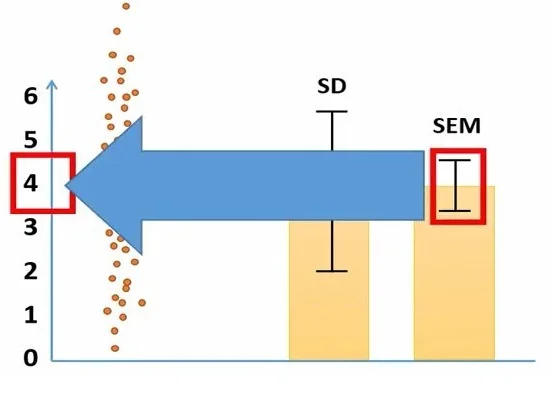
شکل 8. نمایش خطای استاندارد میانگین روی نمودار

در مقایسه با انحراف استاندارد، خطای استاندارد هیچ اطلاعاتی در مورد تنوع داده‌ها در اطراف میانگین ارائه نمی‌دهد. خطای استاندارد بیان می‌کند که چقدر می‌توانیم به میانگین تخمینی از جمعیت اطمینان داشته باشیم (شکل 8).

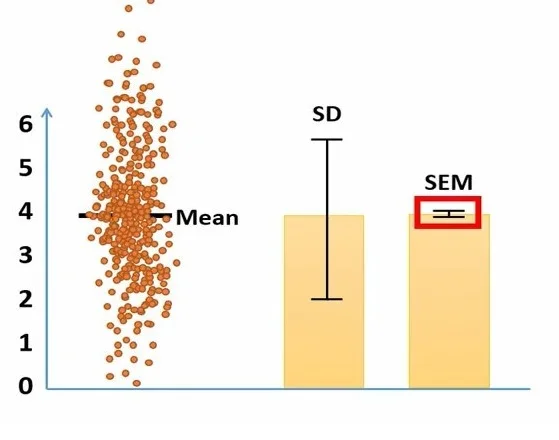
شکل 9. نمایش میانگین،‌انحراف استاندارد و خطای استاندارد در حالت حجم نمونه بالا

چنانچه حجم نمونه ما زیاد باشد و اروربار را به اندازه یک خطای استاندارد از میانگین رسم کرده باشیم، این فاصله را می‌توانیم به این صورت تفسیر کنیم که حدوداً 68 درصد مطمئن هستیم که میانگین حقیقی جامعه در محدوده‌ای بین 3.5 تا 4.5 است(شکل 9).

تفاوت مهم دیگر انحراف استاندارد و خطای استاندارد این است که مقدار خطای استاندارد با افزایش حجم نمونه کاهش می‌یابد. زیرا ما اطمینان بیشتری داریم که میانگین تخمینی ما خیلی به میانگین جمعیت نزدیک است (شکل 9). اما انحراف استاندارد با افزایش حجم نمونه تغییری نمی‌کند. چرا که افزایش حجم نمونه تأثیری بر پراکندگی داده‌ها ندارد.

البته نکته‌ای که باید به آن توجه نمود این است که بالا بودن حجم نمونه باعث دقت زیاد در بدست آوردن انحراف استاندارد می‌شود. بنابراین ما می‌توانیم به انحراف استاندارد تخمینی جامعه از روی نمونه اعتماد بیشتری داشته باشیم.