معیارهای تمایل به مرکز (میانگین ، میانه و مد)

در این مقاله معیارهای تمایل به مرکز شامل میانگین (Mean)، میانه (Median) و مد (Mode) را با مثال بررسی می‌کنیم.

معیارهای تمایل به مرکز

میانگین

میانگین شامل جمع مقادیر تقسیم بر تعداد آن‌هاست که از فرمول زیر محاسبه می‌شود.

مثلاً اگر بخواهیم میانگین قد پنج نفر را بیاوریم باید ابتدا اعداد مربوط به قد این افراد را جمع و تقسیم بر تعداد آن‌ها کنیم (شکل 1).

شکل 1. محاسبه میانگین قد پنج فرد

اگر بخواهیم یک فرمول ریاضی برای محاسبه میانگین بنویسیم بصورت زیر می‌توانیم انجام دهیم.

در این فرمول ایکس-بار نشان دهنده میانگین است. n، نشان دهنده حجم نمونه است. سیگما هم جمع مقادیر را نشان می دهد. پس صورت کسر به ما نشان می‌دهد که باید 5 عدد را با هم جمع کنیم. مخرج کسر نیز بیانگر تعداد اعداد است.

میانه

میانه دقیقاً نقطه وسط داده‌ها را نشان می‌دهد. برای پیدا کردن نقطه وسط داده‌ها باید ابتدا داده‌ها را از کوچک به بزرگ مرتب کرد. سپس داده وسط را از بین داده‌ها انتخاب کرد.

به شکل 2 دقت کنید. برای بدست آوردن میانه، ابتدا داده‌ها را از بزرگ به کوچک مرتب می‌کنیم. سپس نقطه وسط داده‌ها را به عنوان میانه داده‌ها معرفی می‌کنیم. توجه کنید که وقتی تعداد داده‌های ما فرد است،‌ عددی که نصف داده‌ها از آن کوچکتر و نصف دیگر داده‌ها بزرگتر از آن است، میانه نام دارد.

شکل 2. نحوه بدست آوردن میانه در داده‌های با تعداد فرد

وقتی تعداد داده‌های ما زوج است، دو عدد در وسط داده‌ها قرار دارد که میانه از میانگین آن دو عدد حاصل می‌شود (شکل 3).

شکل 3. نحوه بدست آوردن میانه در داده‌های با تعداد زوج

برای توصیف تمایل به مرکز از میانگین استفاده کنیم یا میانه؟

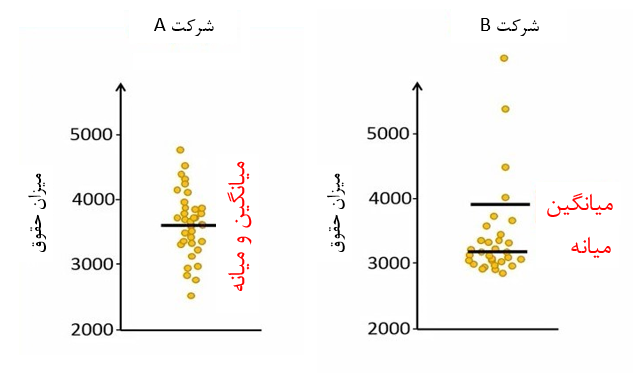
فرض کنید میزان حقوق 40 نفر از کارمندان شرکت A را داریم. داده‌ها را روی یک نمودار پراکنش نمایش می‌دهیم (شکل 4).

شکل 4. میزان حقوق کارکنان شرکت A

در این داده‌ها اگر ما محدوده داده ها را از وسط به دو نیم مساوی تقسیم کنیم، به نظر می رسد که توزیع داده ها در دو ناحیه بالا و پائین توزیع مشابه باشد. بطوریکه هم از نظر فاصله و هم از نظر تعداد، توزیع داده‌ها مشابه است. پس توزیع داده‌های حقوق این 40 کارمند متقارن است.

شکل 5. میزان حقوق کارکنان شرکت B

حالا توزیع حقوق‌ها را در شرکت B ببینید (شکل 5). مطابق شکل 5، توزیع حقوق‌ها در این شرکت نامتقارن است. اگر دقت کنیم، وقتی محدوده داده‌ها را به دو نیم مساوی تقسیم کنیم، داده‌های بیشتری در قسمت پائین نسبت به قسمت بالا وجود دارد.

شکل 6. مقایسه توزیع داده‌ها در دو شرکت A و B

زمانی که داده‌ها توزیع متقارن دارند، میانگین و میانه خیلی به هم نزدیک هستند. ولی زمانی که توزیع داده‌ها چولگی دارد، میانگین تحت تأثیر داده‌های پرت قرار می‌گیرد و از میانه فاصله می‌گیرد (شکل 6).

بطور کلی میانه حساسیت کمتری نسبت به داده‌های پرت دارد. چرا که میانه بر مبنای تعداد داده‌ها محاسبه می‌شود و مقادیر همه داده‌ها روی آن تأثیر ندارد. پس برای داده‌های شرکت A از میانگین به عنوان کمیت تمایل به مرکز استفاده می‌کنیم. در حالی‌که در برای داده‌های شرکت B از میانه به عنوان معیار تمایل به مرکز استفاده می‌کنیم.

نکاتی در مورد میانگین و میانه به عنوان معیارهای تمایل به مرکز

زمانی که توزیع مقادیر ما متقارن یا نرمال است، برای توصیف تمایل به مرکز از میانگین استفاده می‌کنیم.

اما اگر در مقادیر ما اعداد پرت و دورافتاده وجود دارد یا توزیع ما نامتقارن و دارای چولگی است برای توصیف تمایل به مرکز، از میانه استفاده می‌کنیم.

میانگین، تحت تاثیر اعداد پرت قرار می‌گیرد و نسبت به چولگی توزیع بسیار حساس است. در حالی‌که میانه حساسیت کمتری نسبت به اعداد پرت دارد. چرا که میانه بر مبنای تعداد محاسبه می‌شود و مقدار داده‌ها روی آن تاثیر ندارد.

زمانی که مقادیر ما توزیع متقارن دارند میانگین و میانه خیلی به هم نزدیک هستند. لذا می‌توانیم در مقادیر خودمان این دو کمیت را محاسبه کنیم و اگر میانگین و میانه به هم نزدیک بودند برای توصیف تمایل به مرکز از میانگین استفاده کنیم. اما اگر این دو عدد اختلاف زیادی داشتند، از میانه برای توصیف تمایل به مرکز استفاده کنیم.

مد

مد به مشاهده‌ای گفته می شود که بیشترین تکرار را بین مقادیر ما دارد. این کمیت بیشترین کاربرد را برای مقادیر طبقه‌ای دارد. مثلاً می‌توانیم رنگ مورد علاقه 7 نفر را از بین رنگ‌های قرمز، آبی، زرد و مشکی جویا شویم (شکل 7).

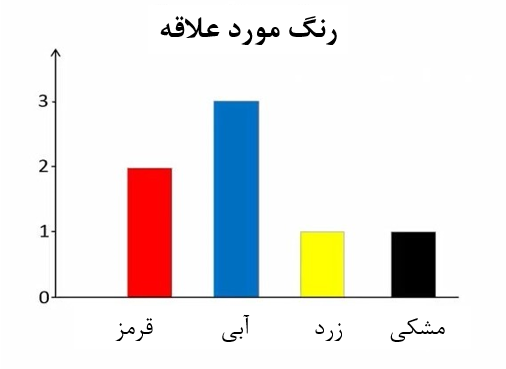
شکل 7. فراوانی افراد بر مبنای رنگ مورد علاقه

اگر 2 نفر رنگ قرمز، 3 نفر رنگ آبی، 1 نفر رنگ زرد و 1 نفر رنگ مشکی را انتخاب کند، رنگ آبی به عنوان مد انتخاب می شود. چرا که بیشترین فراوانی را بین طبقات دارد.