آشنایی با آزمون تی تک نمونه‌ای

در این مقاله آزمون تی تک نمونه‌ای (One sample t-test) را با مثال مورد بررسی قرار می‌دهیم.

برای فهم مطالب این مقاله باید حتماً با توزیع تی آشنا باشید. همچنین نحوه محاسبه میانگین، انحراف استاندارد  و خطای استاندارد را نیز بدانید. لذا ابتدا مقالات مربوط به این مطالب را مطالعه کنید.

مفهوم آزمون تی تک نمونه‌ای

آزمون تی تک نمونه‌ای زمانی استفاده می‌شود که میانگین یک نمونه را با یک مقدار ثابت مقایسه نماییم.

فرمول تی تک نمونه ای به شرح زیر است:

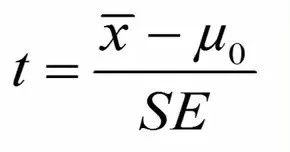
در این فرمول ایکس- بار میانگین را نشان می‌دهد.

مو-صفر نشان دهنده مقدار شناخته شده و استاندارد است.

SE، خطای استاندارد را نشان می‌دهد.

مثال برای آزمون تی تک نمونه‌ای

فرض کنید می‌خواهیم تأثیر یک رژیم غذایی را بر وزن بدن افراد بررسی کنیم. 6 نفر را بطور تصادفی انتخاب و یک نوع رژیم غذایی را به مدت 4 هفته روی این افراد اعمال می‌کنیم. در نهایت میزان تغییر وزن بدن هر یک از افراد را یادداشت می‌کنیم و میانگین می‌گیریم. میانگین تغییر وزن برای مثال ما 0.5- بدست آمد (شکل 1).

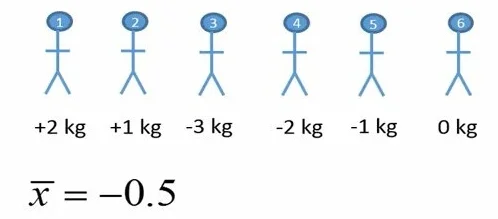
شکل 1. تغییر وزن افراد پس از 4 هفته مصرف رژیم غذایی

محاسبه خطای استاندارد میانگین

پس از محاسبه میانگین، باید خطای استاندارد را محاسبه کنیم. قبلاً در مطلبی نحوه محاسبه و مفهوم دقیق خطای استاندارد را بررسی کرده‌ایم.

خطای استاندارد از تقسیم انحراف معیار به ریشه دوم حجم نمونه بدست می‌آید. با جایگذاری کمیت‌ها در فرمول خطای استاندارد، این عدد 0.763 بدست آمد.

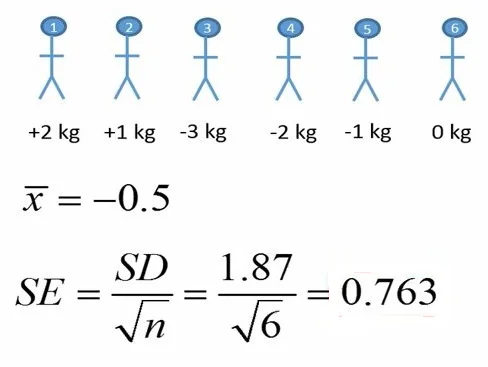
شکل 2. محاسبه خطای استاندارد

مقدار رفرنس (مو-صفر)

به خاطر اینکه می‌خواهیم بدانیم که میانگین وزن بدن افراد پس از مصرف رژیم غذایی تغییر کرده است یا خیر، مقدار رفرنس (مو-صفر) ما صفر است. اگر واقعاً رژیم غذایی موثر باشد، ما در میانگین وزن بدن افراد تغییر مشاهده می‌کنیم که کمتر با بیشتر از مقدار صفر خواهد بود.

محاسبه مقدار تی (t)

با جایگذاری مقادیر میانگین و خطای استاندارد در فرمول آزمون تی تک نمونه‌ای، مقدار تی را محاسبه می‌کنیم. مقدار تی در این مثال 0.655- بدست آمد.

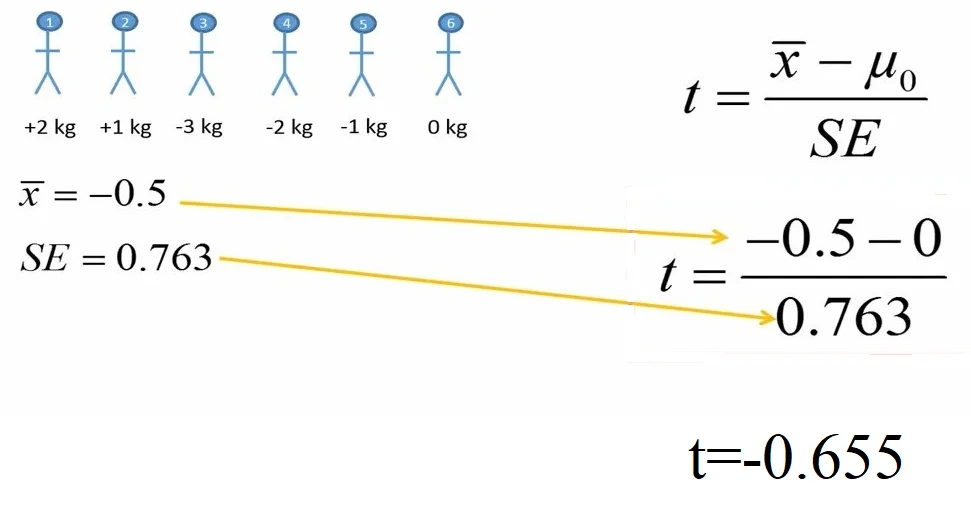
شکل 3. محاسبه مقدار تی در آزمون تی تک نمونه‌ای

پیدا کردن مقدار تی روی توزیع تی و محاسبه مقدار P-value

پس از محاسبه مقدار تی باید به توزیع تی با درجه آزادی 5 مراجعه می‌کنیم و موقعیت 0.655- و 0.655 را در توزیع تی پیدا می‌کنیم. با استفاده از یک نرم افزار آماری سطح زیر نمودار سمت راست و چپ توزیع را محاسبه می‌کنیم. این مقدار برابر با سطح معنی‌داری با P-value ما خواهد بود (شکل 4).

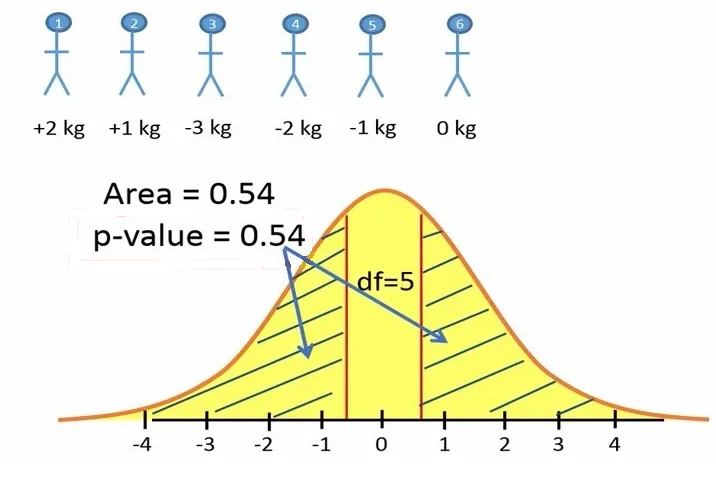
شکل 4. محاسبه مقدار P-value در آزمون تی تک نمونه‌ای

چگونه در آزمون تی تک نمونه‌ای مقدار P-value را تفسیر کنیم؟

اگر فرض کنیم که رژیم غذایی هیچ اثری نداشته است، P-value احتمال اینکه بطور شانسی مشاهده کنیم که رژیم غذایی بر وزن بدن موثر بوده است را نشان می‌دهد.

در مثال ما اگر فرض کنیم که رژیم غذایی تأثیری روی وزن بدن ندارد، احتمال اینکه تفاوت میانگین بین قبل و بعد از دریافت رژیم غذایی 0.5 یا بیشتر باشد، 54 درصد است. پس به احتمال زیاد میانگین تفاوت وزن  بین قبل و بعد از دریافت رژیم غذایی شانسی بوده است.

در آمار اغلب نیاز داریم که به قضاوت خود 95 درصد اطمینان داشته باشیم. بنابراین می‌گوییم، رژیم غذایی تنها در صورتی که P-value کمتر از 0.05 باشد، مؤثر است.

بطور کلی سه حالت می‌تواند برای P-value وجود داشته باشد:

P>0.05 : شواهد کافی برای موثر بودن رژیم غذایی نداریم.

P:0.05-0.01 : شواهد متوسطی مبنی بر تأثیر رژیم غذایی داریم.

P<0.01: شواهد قوی مبنی بر تاثیر رژیم غذایی داریم.

پیدا کردن مقادیر بحرانی توزیع تی

در آزمون تی تک نمونه‌ای برای پی بردن به تأثیر رژیم غذایی بر تغییر وزن افراد، می‌توانیم به جای محاسبه P-value، از مقادیر بحرانی توزیع تی استفاده کنیم. مثلاً مقادیر بحرانی توزیع تی برای پوشش 95% توزیع تی با درجه آزادی 5، اعداد 2.57+ و 2.57- هستند (شکل 5).

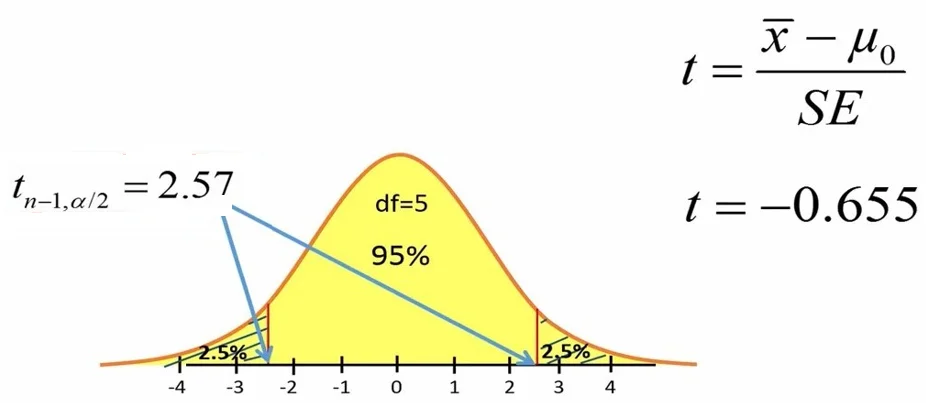
شکل 5. مقادیر بحرانی توزیع تی برای پوشش 95% سطح زیر نمودار در آزمون تی تک نمونه‌ای

بنابراین زمانی که آماره تی محاسبه‌ای در بازه دو مقدار بحرانی قرار گیرد، می‌توانیم بفهمیم که مقدار P-value بزرگتر از 0.05 است و نتیجه بگیریم که رژیم غذایی موثر نبوده است (شکل 6).

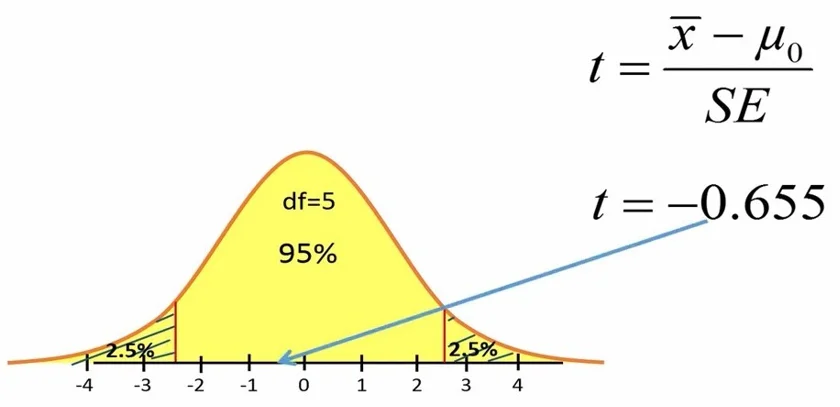
شکل 6. قرار گرفتن مقدار تی در محدوده اطمینان 95%

حالا فرض کنید آماره تی ما به جای عدد 0.655- عدد 3- بدست بیاید، در اینصورت می‌توانیم فرض H0 را رد کنیم و بگوییم رژیم غذایی ما بر تغییر وزن مؤثر بوده است. چون مقدار 3- کوچکتر از مقدار بحرانی 2.57- است و در محدوده 95 % قرار نمی‌گیرد. در کل زمانی که آماره تی خارج از محدوده 95 % قرار می گیرد، می فهمیم که مقدار P-value کمتر از 0.05 است.