مقایسه آزمون تی مستقل با آزمون تی زوجی

در این مقاله آزمون تی مستقل و تی زوجی را با هم مقایسه می‌کنیم. مقایسه این دو آزمون از این نظر مهم است که به هیچ عنوان نباید این دو آزمون به اشتباه به جای یکدیگر استفاده شوند. در غیر اینصورت منجر به نتایج نادرست خواهد شد.

برای فهم تفاوت این دو آزمون ابتدا باید با مفاهیم دو آزمون آشنا باشید.

مثال آزمون تی زوجی

فرض کنید می‌خواهیم تأثیر یک رژیم غذایی را‌ بر وزن 6 فرد بررسی کنیم. به این منظور وزن 6 فرد را قبل و چهار ماه بعد از دریافت رژیم غذایی اندازه‌گیری می‌کنیم.

شکل 1. طرح مطالعه قبل-بعد

در شکل 2، داده‌ها در جدول و همچنین روی نمودار نشان داده شده است.

شکل 2. داده‌ها و نمودار متغیر وزن قبل و بعد از دریافت رژیم غذایی

مطابق شکل 2، میانگین وزن 6 فرد قبل از دریافت رژیم غذایی 81 و انحراف استاندارد آن‌ها 13.14 است. در حالی که میانگین وزن این افراد بعد از دریافت رژیم غذایی 77 و انحراف استاندارد آن‌ها 11.71 حاصل شده است. میانگین تفاوت بین وز‌ن‌ها قبل و بعد از دریافت رژیم غذایی 4- است. بنابراین بطور متوسط افراد، چهار هفته پس از دریافت رژیم غذایی 4 کیلوگرم وزن کم کرده‌اند.

نکته مهم در این آزمایش این است که انحراف استاندارد زمان قبل (13.14) و بعد از دریافت رژیم غذایی (11.71) نسبت به انحراف استاندارد تفاوت‌ها (1.78) اعداد بسیار بالایی را نشان می‌دهد که در ادامه به اهمیت این موضوع پی می‌بریم.

مقایسه آزمون تی مستقل و تی زوجی

الان می‌ خواهیم این آزمایش را بر مبنای هر دو آزمون تی مستقل و تی زوجی تجزیه و تحلیل و تفسیر کنیم و ببینیم این دو آزمون چه تفاوتی دارند.

فرمول آزمون تی مستقل، در صورتی که دو گروه حجم و واریانس برابر داشته باشند به شرح زیر است:

همچنین برای آزمون تی زوجی از فرمول زیر استفاده می‌کنیم.

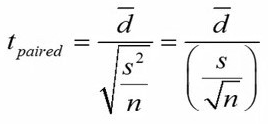
برای آشنایی با اجزای فرمول‌ها به مقالات مربوطه مراجعه نمایید.

توجه کنید که آزمون تی مستقل برای این آزمایش مناسب نیست. چرا که نمونه‌های ما در دو گروه مستقل از هم نیستند. یعنی اندازه گیری وزن بصورت قبل- بعد روی افراد مشابهی انجام شده است.

با این حال برای مقایسه دو آزمون،  ما بطور اشتباه از آزمون تی مستقل به جای تی زوجی استفاده کنیم تا برررسی کنیم چه مشکلی ایجاد می‌شود.

محاسبه مقدار تی مستقل

ابتدا با استفاده مقادیر میانگین و خطای استاندارد، مقدار تی مستقل را محاسبه می‌کنیم. همانطور که در شکل 3 مشاهده می‌کنید، مقدار تی 0.56- بدست آمد.

محاسبه مقدار تی زوجی

حالا با استفاده از فرمول، مقدار تی را محاسبه می‌کنیم.

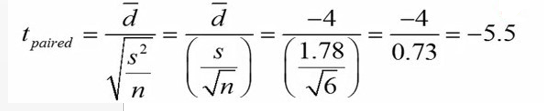
شکل 4. محاسبه مقدار تی در آزمون تی زوجی

مقایسه نهایی دو آزمون

در هر دو فرمول آزمون‌های تی مستقل و تی زوجی، صورت کسر، مشابه است. صورت کسر این دو آزمون، تفاوت میانگین دو نمونه را نشان می‌دهد. همانطور که ملاحظه می‌کنید، تفاوت میانگین دو گروه 4- است که کاملاً در محاسبه دو آزمون مشابه است.

اما در مخرج کسر خطای استاندارد تفاوت‌ها قرار می‌گیرد.

توجه کنید که خطای استاندارد در آزمون تی مستقل 7.2 و در آزمون تی زوجی 0.73 بدست آمد. پس خطای استاندارد در آزمون تی مستقل حدوداً 10 برابر بیشتر از آزمون تی زوجی است. این موضوع باعث می‌شود که مقدار تی در آزمون تی زوجی (5.5-) حدوداً 10 برابر بیشتر از آزمون تی مستقل (0.56-) باشد.

اگر ما مقدار P-value را برای آماره‌های تی محاسبه کنیم، می بینیم که مقدار P-value در آزمون تی زوجی حدوداً 200 برابر کوچکتر از مقدار P-value آزمون تی مستقل است (شکل 5).

پس ما اگر به اشتباه آزمون تی مستقل را به جای آزمون تی زوجی استفاده کنیم، نتیجه می‌گیریم که رژیم غذایی بر وزن افراد موثر نبوده است. در حالی‌که با آزمون تی زوجی فرض صفر رد و تأثیر رژیم غذایی کاملاً محرز است.

نتیجه می‌گیریم که اگر به نحوی داده‌های دو گروه ارتباط داشتند، حتماً باید از آزمون تی زوجی استفاده کنیم. تنها در صورتی از آزمون تی مستقل استفاده می‌کنیم که افراد دو گروه کاملاً مستقل از هم باشند.

تفاوت مهم دیگر بین دو آزمون تی مستقل و تی زوجی، مفروضات نرمالیتی است. زمانی که ما از آزمون تی مستقل استفاده می کنیم عموماً فرض می‌کنیم که مشاهدات در دو گروه توزیع نرمال دارند. در حالی‌که در آزمون تی زوجی فرض می‌کنیم که تفاوت ها دارای توزیع نرمال هستند.