آشنایی با آنالیز واریانس با اندازههای تکراری
در این مقاله آنالیز واریانس با اندازههای تکراری (repeated measures ANOVA) را با هم یاد میگیریم.
قبل از مطالعه این مقاله لطفا مقالات مربوط به آزمونهای تی مستقل، تی زوجی و آنالیز واریانس یکطرفه (قسمت اول و دوم) را ببینید. پس از آن این مقاله را پیگیری نمایید.
مفهوم دقیق آنالیز واریانس با اندازههای تکراری
آنالیز واریانس با اندازههای تکراری گسترش یافته آزمون تی زوجی است. اگر خاطرتان باشد در جلسه مربوط به آزمون تی زوجی مثالی در مورد تفاوت وزن افراد قبل و چهار هفته پس از دریافت رژیم غذایی را بررسی کردیم. در نهایت متوجه شدیم که آیا رژیم غذایی موثر بوده است یا خیر؟
در آنالیز واریانس با اندازههای تکراری هم آزمون مشابهی انجام میدهیم. اما به جای اینکه اندازهگیری وزن تنها در دو زمان انجام شده باشد، اندازهگیریها در سه و بیشتر از سه زمان انجام میشود. در شکل 1 اندازهگیری وزن در مورد آزمون تی زوجی و آنالیز واریانس اندازههای تکراری را نشان دادهام.

شکل 1. مقایسه تی زوجی و آنالیز واریانس اندازههای تکراری
همان طور که در شکل 1 ملاحظه میکنید، برای آنالیز واریانس با اندازههای تکراری اندازهگیری وزن را در سه زمان انجام دادهایم در حالیکه برای آزمون تی زوجی اندازهگیری وزن را در دو زمان انجام دادهایم.
مقایسه آنالیز واریانس یکطرفه و آنالیز واریانس با اندازههای تکراری
مقایسه آنالیز واریانس یکطرفه و آنالیز واریانس با اندازههای تکراری را در شکل 2 نشان دادهام.

شکل 2. مقایسه آنالیز واریانس با اندازههای تکراری و آنالیز واریانس بکطرفه
مطابق شکل 2، نسبت F در آنالیز واریانس یکطرفه بر مبنای واریانس بین و درون گروهی محاسبه میشود. اما در آنالیز واریانس با اندازههای تکراری، ابتدا واریانس درون گروهی به دو گروه واریانس افراد و واریانس خطا تقسیم میشود. واریانس خطا تنوعی است که پس از حذف تنوع بین افراد باقی میماند. نسبت F نیز از تقسیم تنوع بین گروهها به واریانس خطا حاصل میشود.
پس تفاوت بین آنالیز واریانس یکطرفه و آنالیز واریانس با اندازههای تکراری در مخرج کسر F است. در آزمون آنالیز واریانس با اندازههای تکراری در مخرج کسر F تنوع بین افراد را حذف میکنیم.
آزمون فرضیات برای آزمون آنالیز واریانس با اندازههای تکراری
فرض صفر (H0) در آنالیز واریانس مکرر گزاره ای است که بیان میکند میانگین K گروه با هم برابر است. در حالیکه فرض مقابل (H1) بیان میکند که حداقل یکی از میانگینها با بقیه متقاوت است.
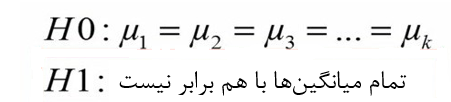
مثال برای آنالیز واریانس با اندازههای تکراری
فرض کنید وزن چهار فرد را قبل، دو هفته و چهار هفته پس ار دریافت رژیم غذایی اندازهگیری کردهایم. دادهها را در شکل 3 در قالب جدول و نمودار نشان دادهام.
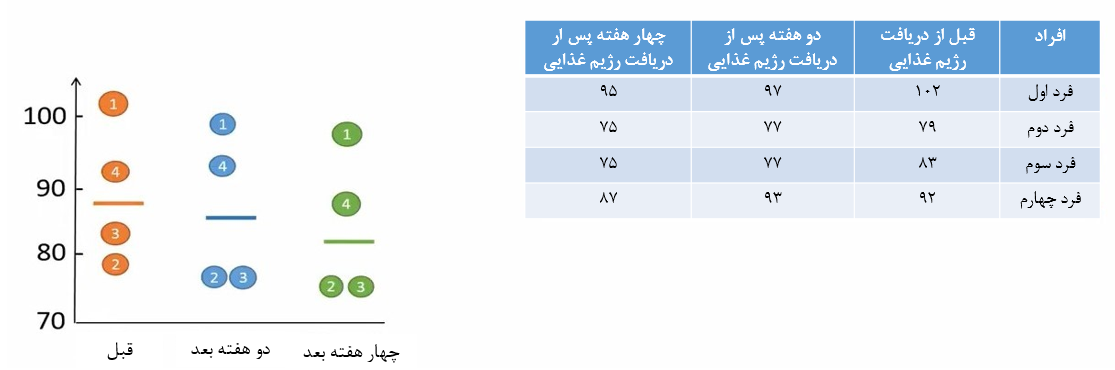
شکل 3. دادههای وزن چهار فرد، قبل، دو و چهار هفته بعد از دریافت رژیم غذایی
مثلاً نفر اول قبل از دریافت رژیم غذایی 102 کیلوگرم وزن داشته است. دو هفته پس از دریافت رژیم غذایی وزن این فرد 97 کیلوگرم و چهار هفته پس از دریافت رژیم غذایی وزن 95 کیلوگرم شده است. مقدار تغییر وزن سایر افراد را نیز در شکل 3 آوردهام.
نوشتن آزمون فرضیات
برای اینکه ببینیم آیا واقعاً رژیم غذایی مؤثر بوده است یا خیر؟ ابتدا آزمون فرضیات و سطح خطا را مشخص میکنیم.

فرض صفر (H0) گزارهای است که نشان میدهد میانگین وزن جمعیت قبل، دو هفته و چهار هفته پس از دریافت رژیم غذایی ثابت باقی مانده است.
محاسبات آنالیز واریانس با اندازههای تکراری
مانند آنچه در جلسه مربوط به آنالیز واریانس یکطرفه گفتیم، ابتدا یک جدول آنالیز واریانس با اندازههای تکراری رسم میکنیم. (شکل 4).
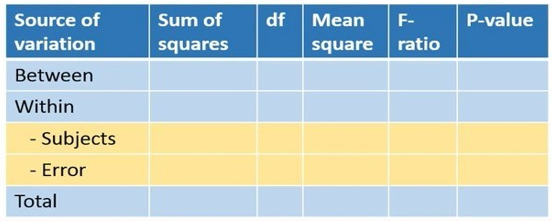
شکل 4. جدول آنالیز واریانس با اندازههای تکراری
تفاوت آنالیز واریانس یکطرفه با آنالیز واریانس با اندازههای تکراری این است که در آنالیز واریانس مکرر مجموع مربعات درون گروهها به دو قسمت تنوع بین افراد و خطا تقسیم میشود. در حقیقت خطا نوعی تنوع است که پس از حذف واریانس مربوط به افراد باقی میماند (شکل 4).
محاسبه میانگین هر گروه
ابتدا باید میانگین وزن هر گروه را محاسبه کنیم. میانگین وزن چهار فرد قبل از دریافت رژیم غذایی 89 کیلوگرم میباشد. پس از دو هفته مصرف رژیم غذایی میانگین وزن افراد به 86 کیلوگرم کاهش یافته است. پس از 4 هفته از مصرف رژیم غذایی میانگین وزن افراد به 83 کیلوگرم کاهش پیدا کرده است (شکل 5).
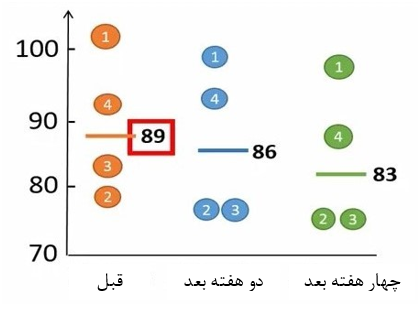
شکل 5. محاسبه میانگین هر گروه
محاسبه میانگین کل
در مرحله دوم باید میانگین کل را محاسبه کنیم. میانگین کل برابر با 86 میشود شکل 6).

شکل 6. محاسبه میانگین کل
محاسبه مجموع مربعات درون گروهها
مجموع مربعات درون گروهها را مانند آنچه در آنالیز واریانس یکطرفه انجام دادیم، محاسبه میکنیم. به این منظور باید ابتدا تفاوت هر فرد نسبت به میانگین گروه خودش محاسبه شود. بعد این تفاوت ها به توان دو برسد و با هم جمع شود. مجموع مربعات درون گروهها را در این مثال ما 934 بدست آوردهایم(شکل 7).
نکته مهم: واریانس گروه اول تنوع وزنها بین افراد قبل از مصرف رژیم غذایی را نشان میدهد. این واریانس ربطی به تأثیر رژیم غذایی ندارد. یکی از مزیتهای مهم طرح آنالیز واریانس تکراری حذف این واریانس است که در مراحل بعد انجام میدهیم.
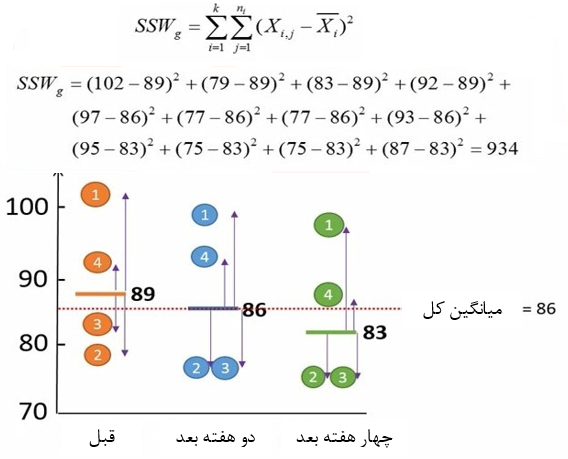
شکل 7. محاسبه مجموع مربعات درون گروهها
محاسبه مجموع مربعات بین گروهها
برای محاسبه مجموع مربعات بین گروهها، ابتدا تفاوت میانگین هر گروه را نسبت به میانگین کل محاسبه میکنیم. این تفاوتها را به توان دو میرسانیم. حاصل بدست آمده را در حجم نمونه هر گروه ضرب میکنیم و در نهایت تمام اعداد حاصل شده را با هم جمع میکنیم. در مثال ما مجموع مربعات بین گروهها عدد 72 بدست آمد (شکل 8).

شکل 8. محاسبه مجموع مربعات بین گروهها
محاسبه مجموع مربعات کل
مجموع تنوع بین و درون گروهها واریانس کل را تشکیل میدهد. واریانس کل را میتوانیم از مجموع مربع تفاوت هر مشاهده نسبت به میانگین کل محاسبه کنیم. برای مثال ما مجموع مربعات کل 1006 بدست آمد (شکل 9).
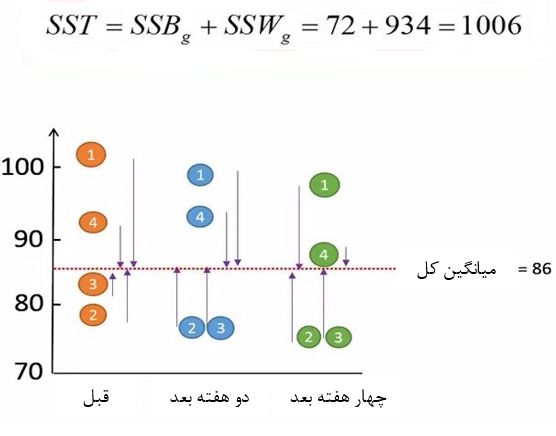
شکل 9. محاسبه مجموع مربعات کل
محاسبه مجموع مربعات بین افراد
برای محاسبه مجموع مربعات افراد، ابتدا تفاوت میانگین اعداد مربوط به هر فرد را نسبت به میانگین کل محاسبه میکنیم. این تفاوتها را به توان دو میرسانیم. حاصل بدست آمده را در تعداد اعداد مربوط به هر فرد ضرب میکنیم. در نهایت تمام اعداد حاصل شده را با هم جمع میکنیم. در مثال ما مجموع مربعات بین افراد 916.67 بدست آمد (شکل 10).
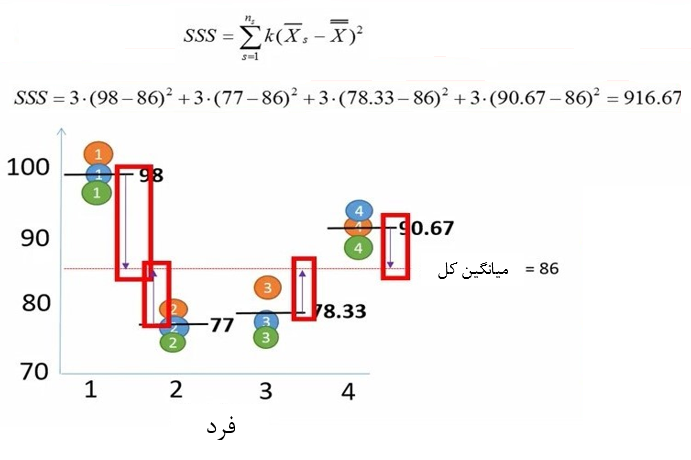
شکل 10. محاسبه مجموع مربعات هر فرد
محاسبه مجموع مربعات خطا
اگر مجموع مربعات افراد را از مجموع مربعات درون گروهها کم کنیم مجموع مربعات خطا (SSE) بدست میآید. در مثال ما مجموع مربعات خطا 17.33 بدست آمد.
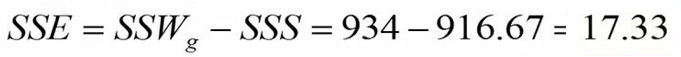
در نهایت مجموع مربعات تمام منابع تغییرات را در جدول آنالیز واریانس وارد میکنیم.
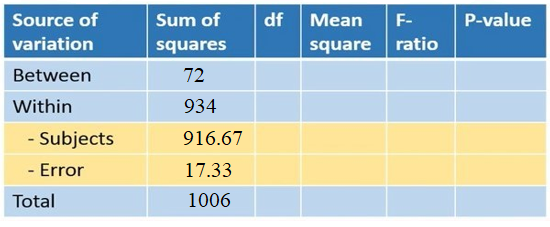
شکل 11. ورود مجموع مربعات تمام منابع تغییرات به جدول آنالیز واریانس مکرر
محاسبه درجه آزادی (df)
ستون سوم در جدول آنالیز واریانس مربوط به درجه آزادی (df) است. برای آشنایی با درجه آزادی به مقاله مربوط به آن مراجعه کنید.
درجه آزادی منبع تغییر بین گروهها (Between) تعداد گروه منهای 1 است. چون سه گروه داشتیم، درجه آزادی بین گروهها 2 میشود.
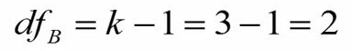
درجه آزادی درون گروهها (Within) برابر با تعداد کل دادهها منهای تعداد گروهها است. ما کلاً 12 داده و 3 گروه داریم. پس درجه آزادی درون گروهها 9 بدست میآید.
![]()
درجه آزادی بین افراد (Subjects)، تعداد افراد منهای 1 است. چون ما چهار فرد در آزمایش داشتیم، درجه آزادی بین افراد 3 میشود.
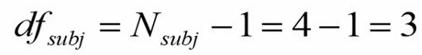
درجه آزادی خطا (Error) برابر با درجه آزادی درون گروهها منهای درجه آزادی افراد است. درجه آزادی درون گروهها 9 و درجه آزادی افراد 3 است. پس درجه آزادی خطا 6 بدست میآید.

درجه آزادی کل (Total) نیز برابر با تعداد کل دادهها منهای 1است. چون 12 داده داشتیم، درجه آزادی کل 11 بدست میآید (شکل 12).
![]()
تا اینجا درجه آزادیها را هم وارد جدول آنالیز واریانس میکنیم (شکل 12).

شکل 12. ورود درجه آزادی به جدول آنالیز واریانس
محاسبه میانگین مربعات (Mean square)
برای محاسبه میانگین مربعات، باید مجموع مربعات تمام منابع تغییرات را تقسیم بر درجه آزادی (df) کنیم. مثلاً میانگین مربعات بین گروهها 72 تقسیم بر 2، عدد 36 میشود. به همین ترتیب میانگین مربعات تمام منابع تغییرات را محاسبه و گزارش میکنیم (شکل 13).
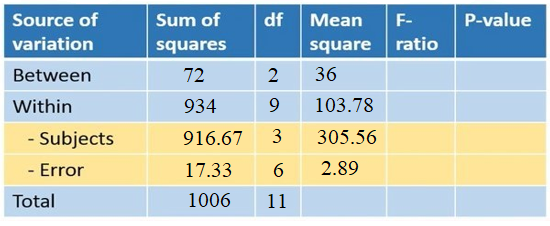
شکل 13. ورود میانگین مربعات به جدول آنالیز واریانس مکرر
محاسبه آماره F
برای محاسبه آماره F باید میانگین مربعات هر گروه را تقسیم بر میانگین مربعات خطا کنیم (شکل 14). محاسبه نسبت F بین گروهها برای ما مهم است. این عدد برای مثال ما 12.46 حاصل شده است. ما از توزیع F با درجه آزادی 2 و 6 استفاده میکنیم تا ببینیم مقدار F از مقدار بحرانی کوچکتر یا بزرگتر است. یا میتوانیم مقدار P-vaule برای F محاسبه شده را با استفاده از یک نرم افزار آماری محاسبه کنیم. در این مثال مقدار P-value را ما عدد 0.0073 بدست آوردهایم (شکل 14).

شکل 14. محاسبه نسبت F و مقدار P-value به جدول آنالیز واریانس با اندازههای تکراری
نتیجهگیری نهایی
چون مقدار P-value از مقدار آلفا کوچکتر است، میتوانیم فرض صفر (H0) مبنی بر تساوی میانگین جمعیتها را رد کنیم. نتیجه میگیریم که حداقل بین میانگین دو گروه تفاوت معنیدار آماری وجود دارد.

انجام آزمونهای تعقیبی (Post hoc tests)
برای اینکه ببینیم کدام دو میانگین تفاوت معنیدار دارند، باید مقایسات زوجی بین گروهها انجام دهیم (شکل 15). این کار با استفاده از آزمونهای مختلف انجام میشود که هر کدام ویژگی مربوط به خود را دارند و در مباحث جداگانهای به آنها خواهیم پرداخت.
فعلاً با استفاده از آزمون حداقل تفاوت معنیدار (LSD) مقایسه میانگین را انجام میدهیم. این آزمون مقادیر P-value را تصحیح نمیکند.
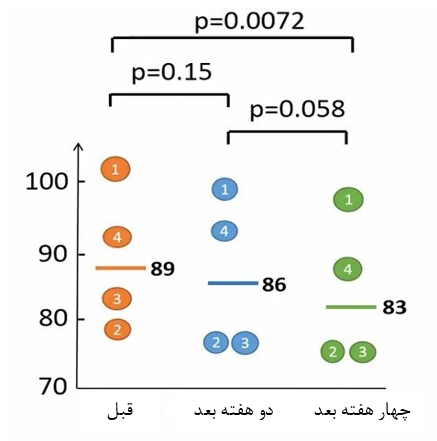
شکل 15. مقایسات زوجی بین زمانها
مطابق شکل 15، تنها تفاوت معنیدار، تفاوت بین زمان اول و سوم است. بنابراین میتوانیم نتیجه بگیریم که رژیم غذایی پس از چهار هفته وزن افراد را نسبت به زمان اول کاهش داده است.
مقایسه جدول آنالیز واریانس یکطرفه و آنالیز واریانس با اندازههای تکراری
فرض کنید ما به جای آنالیز واریانس با اندازههای تکراری از آنالیز واریانس یکطرفه برای آنالیز دادهها استفاده میکردیم. نتایج این دو آزمون را در شکل 16 مشاهده میکنید.
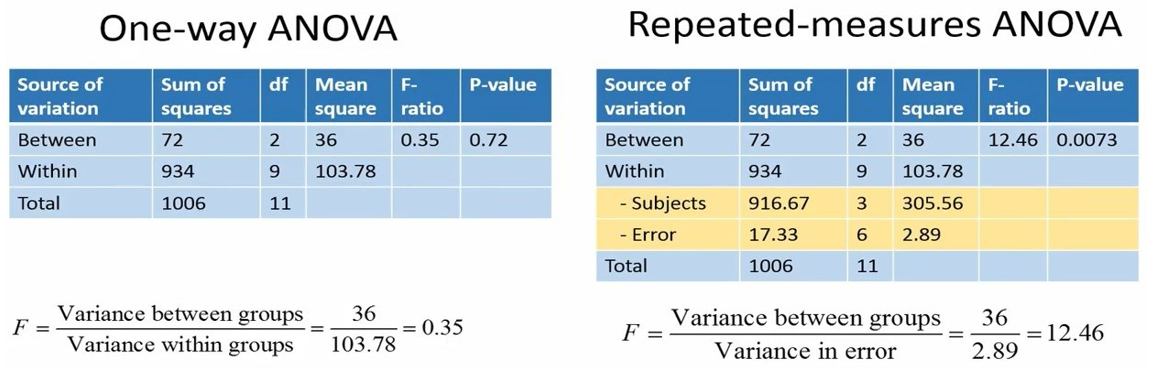
شکل 16. مقایسه نتایج آنالیز واریانس یکطرفه با آنالیز واریانس با اندازههای تکراری
مطابق شکل 16، اگر ما به جای آنالیز واریانس با اندازههای تکراری، از آنالیز واریانس یکطرفه استفاده میکردیم، نمیتوانستیم فرض صفر (H0) را رد کنیم و به اشتباه نتیجه میگرفتیم که رژیم غذایی ما روی وزن افراد مؤثر نبوده است. چرا که مقدار P-value در صورت استفاده از آنالیز واریانس یکطرفه 0.72 بدست میآید. در حالیکه مقدار P-value در صورت استفاده از آنالیز واریانس با اندازههای تکراری 0.0073 حاصل میشود که کوچکتر از 0.05 میباشد.
این موضوع به این دلیل است که در آنالیز واریانس مکرر، در مخرج کسر F خطا قرار دارد. در حالیکه در آنالیز واریانس یکطرفه، در مخرج کسر F واریانس بین گروهها قرار دارد. در حقیقت در آنالیز واریانس با اندازههای تکراری ما واریانس بین افراد را حذف کردهایم و به این ترتیب خطای آزمایش را کاهش دادهایم.
پس به این ترتیب به اهمیت استفاده صحیح از آنالیز واریانس با اندازههای تکراری نسبت به آنالیز واریانس یکطرفه پی میبریم.
مفروضات آنالیز واریانس با اندازههای تکراری
پیش فرض اصلی آنالیز واریانس با اندازههای تکراری آزمون کروویت (Sphericity test) است. کروویت یعنی واریانس تفاوت بین گروهها باید از نظر آماری تفاوت نداشته باشد. به عنوان مثال ابتدا تفاوت بین گروههای اول-دوم، اول-سوم و دوم-سوم را محاسبه میکنیم. سپس واریانس تفاوتها را محاسبه میکنیم (شکل 17).
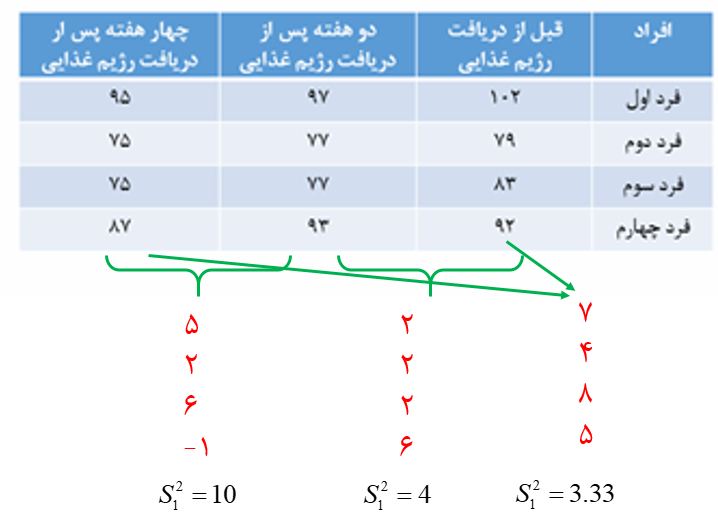
شکل 17. محاسبه تفاوتها و واریانس آنها به منظور انجام آزمون کروویت
مطابق شکل 17، واریانس تفاوتها در زمان اول نسبت به زمان دوم و سوم خیلی بیشتر است. اما باید معنیداری تفاوتها با استفاده از آزمون کروویت ماچلی بررسی شود. فرض صفر (H0) برای این آزمون برابری واریانس تفاوتها و وجود کروویت را نشان میدهد. اگر مقدار P-value کوچکتر از 0.05 باشد نشان دهنده نبود کروویت در دادهها است.

برای این مثال ما مقدار P-value را 0.46 بدست آوردهایم. این موضوع به این معنی است که مفروض کروویت در دادههای ما وجود دارد و میتوانیم آنالیز واریانس با اندازههای تکراری انجام دهیم. چنانچه مفروض کروویت در دادهها وجود نداشته باشد باید درجه آزادی در جدول انالیز واریانس درون آزمودنیها را بر مبنای روشهایی مانند گرین هاوس گیزر، هین-فلت یا حد پائین تصحیح کنیم.

نظرات :