آشنایی با آنالیز واریانس یکطرفه (قسمت اول)

در این مقاله در مورد مفهوم آنالیز واریانس یکطرفه (One-way ANOVA) با شما صحبت می‌کنیم. در مقاله دوم از مبحث ANOVA، محاسبات ریاضی آنالیز واریانس یکطرفه را انجام خواهیم داد.

کاربرد آنالیز واریانس یکطرفه

وقتی اثر یک عامل در آزمایش سنجش می‌شود، از آنالیز واریانس یکطرفه استفاده می‌کنیم. اگر ما اثر دو یا چند عامل را در آزمایش بررسی کنیم، آنالیز واریانس دو یا چندطرفه خواهیم داشت.

مثال آنالیز واریانس یکطرفه

فرض کنید داده‌های فشار خون 12 فرد در سه گروه سنی 35-20 سال (جوان)، 55-36 سال (میان‌سال) و بزرگتر از 55 سال (سالمند) را اندازه‌گیری کرده‌ایم. هدف از این آزمایش این است که آیا فشار خون بین گروه‌های مختلف سنی تفاوت دارد؟

در این مثال طرح آزمایشی ما متعادل است چرا که تعداد مساوی از مشاهدات در گروه‌ها وجود دارد. به این صورت که در هر گروه سنی چهار نفر حضور دارند (شکل 1).

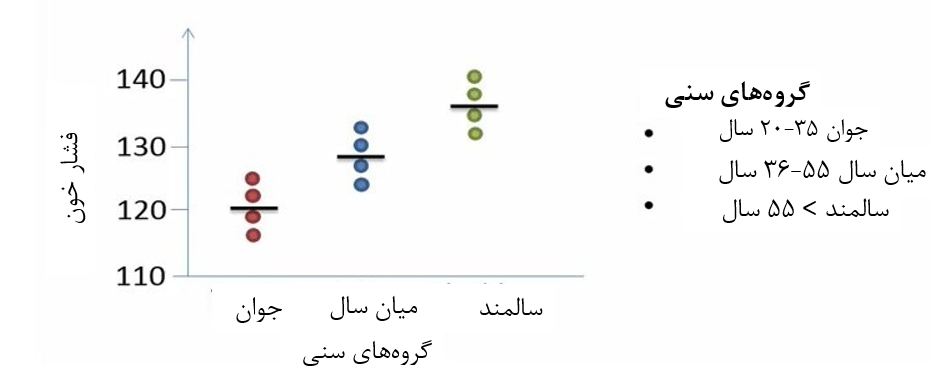
شکل 1. فشار خون در سه گروه سنی

چه زمانی از آنالیز واریانس یکطرفه (one-way ANOVA) استفاده می‌کنیم؟

آنالیز واریانس یکطرفه زمانی استفاده می‌شود که ما بخواهیم میانگین سه و بیشتر از سه گروه مستقل را مقایسه کنیم.

باید توجه داشته باشیم که متغیر وابسته (متغیر اندازه گیری شده) باید از نوع کمی پیوسته باشد. همچنین متغیر مستقل ما باید طبقه‌ای باشد. در این مثال متغیر وابسته ما فشار خون است که با مقیاس میلی‌متر جیوه اندازه‌گیری کرده‌ایم. متغیر مستقل ما گروه‌های سنی است که سه طبقه دارد.

نکته: آنالیز واریانس می‌تواند برای مقایسه دو گروه نیز مورد استفاده قرار گیرد که نتایج آن دقیقاً مشابه با آزمون تی مستقل خواهد بود.

مقایسه آزمون تی مستقل (غیر زوجی) و آنالیز واریانس یکطرفه

زمانی که دو گروه مستقل داریم، برای مقایسه آن‌ها از آزمون تی مستقل استفاده می‌کنیم. حال اگر ما به جای آزمون تی مستقل از آنالیز واریانس یکطرفه استفاده کنیم، به جای آماره t، آماره F خواهیم داشت. در این صورت رابطه بین آماره F و t بصورت زیر می‌باشد:

F=t²

در مثال ما اگر گروه سوم را نادیده بگیریم و دو گروه اول و دوم را با آزمون تی مستقل و آنالیز واریانس یکطرفه مقایسه کنیم، رابطه مذکور را می‌توانیم مشاهده کنیم.

مثلاً اگر دو گروه اول و دوم را از نظر متغیر فشار خون با استفاده از آزمون تی مستقل مقایسه کنیم، مقدار آماره تی 2.74- بدست می‌آید. مقدار P-value نیز 0.034 بدست می‌آید. در حالی‌که در آزمون آنوا (ANOVA) مقدار F، 7.5 و مقدار P-value همان عدد 0.034 حاصل می‌شود. اگر آماره تی که 2.74- است را به توان دو برسانیم، عدد 7.5 حاصل می‌شود.

مقایسه توزیع تی (t) و توزیع اف F

دو آزمون t و F محاسبات متفاوتی دارند و بر مبنای توزیع‌های متفاوتی هستند. نکته مهم در مورد این دو توزیع این است که توزیع t دارای دو انتها (دو دم) است. اما توزیع F (اف) دارای یک دم در سمت راست است (شکل 2).

شکل 2. مقایسه توزیع تی (t) و توزیع اف (F)

نحوه تبدیل توزیع تی (t) به توزیع اف (F)

زمانی که ما فقط دو گروه داریم، توزیع اف (F) می‌تواند برابر با توزیع مقادیر تی به توان دو باشد. به شکل 3 دقت کنید. مثلاً اگر ما صد هزار مقدار تی از توزیع تی با درجه آزادی 5 داشته باشیم، حدود نیمی از مقادیر مثبت و نیمی از مقادیر منفی هستند. اگر ما این مقادیر را به توان دو برسانیم،‌ فقط مقادیر مثبت خواهیم داشت که توزیعی شبیه توزیع اف (F) با درجه آزادی 1 و 5 خواهیم داشت. درجه آزادی اضافی برای توزیع اف (F) برابر با تعداد گروه‌ها منهای یک است. چون ما دو گروه داشته‌ایم پس درجه آزادی اول در توزیع F عدد 1 خواهد بود.

شکل 3. نحوه تبدیل توزیع تی (t) به توزیع اف (F)

آزمون فرضیات در توزیع تی (t) و توزیع اف (F)

چون توزیع تی مقادیر مثبت و منفی دارد فرضیات ما در آزمون تی می‌تواند یکطرفه یا دوطرفه باشد. در حالی‌که برای توزیع اف (F) فقط می‌توانیم از فرضیات یکطرفه استفاده کنیم (شکل 4).

بنابراین آنالیز واریانس یکطرفه می‌تواند آزمون کند که آیا تفاوت بین میانگین‌ها وجود دارد یا خیر؟ اما آزمون تی علاوه بر اینکه می‌تواند تفاوت بین دو میانگین را آزمون کند، می‌تواند آزمون کند که آیا میانگین یک گروه نسبت به گروه دیگر بزرگتر یا کوچکتر است؟

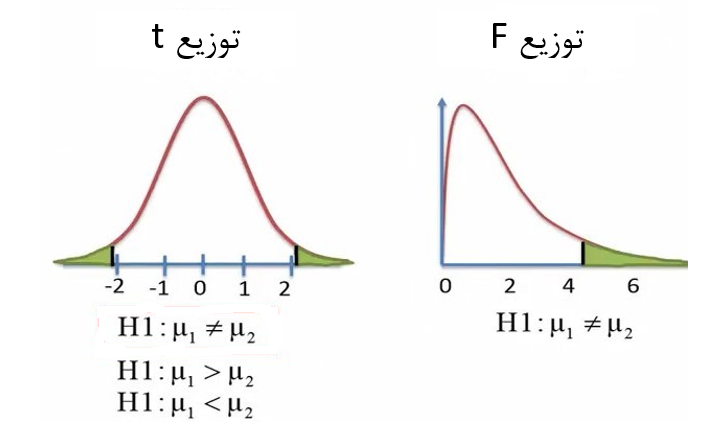
شکل 4. آزمون فرضیات برای توزیع تی (t) و توزیع (F)

چرا به جای آنالیز واریانس یکطرفه از چند آزمون تی مستقل استفاده نمی‌کنیم؟

به شکل 5 دقت کنید. فرض کنید برای مقایسه سه گروه به جای آنالیز واریانس یکطرفه از آزمون تی مستقل استفاده کنیم. در این حالت اگر سه گروه داشته باشیم سه نوع مقایسه خواهیم داشت که در کنار شکل 5 مقایسات را نوشته‌ایم.

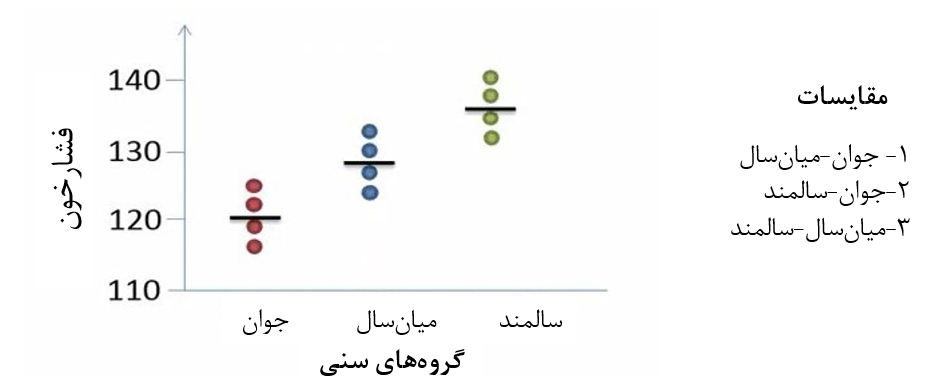
شکل 5. مقایسات زوجی در آزمون تی مستقل

در هر مرتبه استفاده از آزمون تی مستقل جهت انجام مقایسات میانگین، به میزان 5 درصد ریسک خطای نوع اول متحمل می‌شویم. چون سه بار باید آزمون تی مستقل را انجام دهیم نهایتاً ریسک ارتکاب خطای نوع اول ما افزایش می‌یابد. این ریسک را می‌توان از فرمول زیر محاسبه نمود.

در این فرمول آلفا سطح معنی‌داری و K تعداد مقایسات است.

اگر در این مثال ریسک ارتکاب خطای نوع اول را محاسبه کنیم، عدد 0.14 بدست می‌آید.

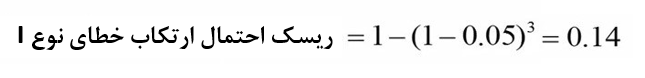
خطای نوع اول خطایی است که ما زمانی مرتکب می‌شویم که فرض صفر (H0) ما واقعاً صحیح باشد ولی ما به اشتباه آن را رد کنیم. به عنوان مثال اگر واقعاً بین دو میانگین جمعیت تفاوت نباشد ولی ما به اشتباه نتیجه بگیریم که تفاوت وجود دارد، مرتکب خطای نوع اول شده‌ایم.

چون در این آزمایش ما سه مقایسه داریم، ریسک ارتکاب خطای نوع اول 0.14 می شود. پس در این مثال اگر ما به جای استفاده از آنالیز واریانس یکطرفه از سه آزمون تی مستقل استفاده کنیم، آلفای ما دیگر 0.05 نیست. به همین دلیل برای ثابت کردن احتمال خطا در سطح 5 درصد باید از آنالیز واریانس یکطرفه استفاده کنیم.

مزیت‌های مهم آزمون ANOVA نسبت به آزمون t-test

1. آنالیز واریانس یکطرفه (ANOVA) تمام میانگین‌ها را همزمان مقایسه می‌کند. بنابراین خطای نوع اول در سطح پنج درصد حفظ می‌شود.
2. ANOVA نسبت به t-test راحت‌تر انجام و تفسیر می‌شود.

آزمون فرضیات در ANOVA

برای آنالیز واریانس یکطرفه می‌توانیم آزمون فرضیات را به شکل زیر بنویسیم.

در این مثال فرض صفر (H0) بیان می‌کند که میانگین فشار خون سیستولیک در سه گروه سنی مشابه است. در حالی‌که فرض یک بیان می کند که حداقل یک گروه میانگین فشار خونی متفاوت از سایر گروه ها دارد.

نکته: فرض H1 نمی‌تواند اینطور بیان شود که کدام میانگین نسبت به دیگری بزرگتر است. پس اگر فرض صفر (H0) ما در آزمون ANOVA رد شود، ما آزمون‌هایی موسوم به آزمون‌های تعقیبی انجام می‌دهیم تا متوجه شویم که کدام میانگین نسبت به سایر میانگین‌ها متفاوت است.

اما اگر نتوانیم فرض صفر را رد کنیم، آزمون تعقیبی انجام نمی‌دهیم چرا که ANOVA به ما می‌گوید بین میانگین‌ها تفاوت وجود ندارد.

مفروضات اصلی آزمون ANOVA

برای انجام آنالیز واریانس یکطرفه باید مفروضات زیر برقرار باشد:

• متغیر وابسته درون هر گروه باید توزیع نرمال داشته باشد.
• واریانس گروه‌ها باید مشابه باشد (همگنی واریانس‌ها ).
• مشاهدات باید مستقل باشند.

توضیح مفروض اول :

مشاهدات در درون هر گروه باید توزیع نرمال داشته باشند. اما درنظر داشته باشید. اگر این مفروض با شواهد قوی رد شود،‌ دو راهکار برای آنالیز داده‌ها داریم. اول استفاده از معادل ناپارامتریک آزمون ANOVA یعنی آزمون کروسکال والیس است. دومین راهکار می‌تواند تبدیل داده‌ها باشد. گاهی اوقات با تبدیل داده‌ها می‌توانیم توزیع آن‌ها را به توزیع نرمال تبدیل کنیم.

توضیح مفروض دوم

واریانس گروه‌ها باید مشابه باشد آزمون لِوِن (Levene’s test) برای این این مفروض استفاده می‌شود. در صورت رد این مفروض با شواهد قوی، می‌توانیم به جای آنالیز واریانس یکطرفه از آزمون ولش آنوا (Welch’s ANOVA) استفاده کنیم.

توضیح مفروض سوم

اگر افراد استفاده شده در آزمایش بطور تصادفی از جمعیت انتخاب شده‌ باشند و واحد‌های آزمایشی کاملاً از هم مستقل باشند این مفروض رعایت شده است. اما اگر مثلاً یک اندازه گیری در طول زمان روی یک نفر (واحد آزمایشی) تکرار شود، مشاهدات از هم مستقل نیستند و باید از تحلیل واریانس با اندازه‌های مکرر استفاده نمود.

آنالیز واریانس یکطرفه چگونه انجام می‌شود؟

گام اول برای انجام آنالیز واریانس یکطرفه، محاسبه میانگین هر گروه است. در مثال ما میانگین فشار خون هر گروه سنی بطور جداگانه محاسبه می‌شود (شکل 6).

شکل 6. میانگین فشار خون در گروه‌های مختلف سنی

گام دوم محاسبه میانگین کل گروه‌ها است. در مثال ما میانگین 12 فرد شرکت کننده در آزمایش محاسبه می‌شود. این میانگین را روی شکل 7 با خط چین قرمز نشان داده‌ایم.

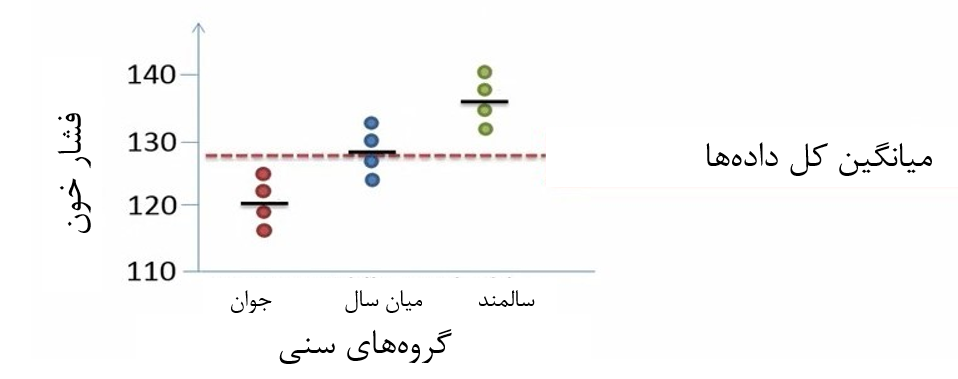
شکل 7. میانگین فشار خون کل افراد

گام سوم محاسبه واریانس ادغام شده درون گروه است. این واریانس در مخرج کسر F قرار می‌گیرد. این کار بر مبنای فاصله مشاهدات از میانگین گروه خودشان انجام می‌شود و در نهایت از واریانس‌ها میانگین وزنی گرفته می‌شود (شکل 8).

شکل 8. محاسبه واریانس درون گروه‌ها

گام چهارم محاسبه واریانس بین گروه‌ها است. این واریانس در صورت کسر F قرار می‌گیرد. برای محاسبه آن باید فاصله بین میانگین هر گروه نسبت به میانگین کل سنجش شود (شکل 9).

شکل 9. محاسبه واریانس بین گروه‌ها

در نهایت می‌توانیم آماره F را محاسبه کنیم. اگر مقدار P-value محاسبه شده کمتر از 0.05 باشد، فرضیه صفر را در سطح 0.05 رد می‌کنیم. بطور خلاصه ما فرض صفر را فقط در صورتی می‌توانیم رد کنیم که واریانس بین گروه ها به حد کافی بزرگتر از واریانس درون گروه ها باشد (شکل 10).

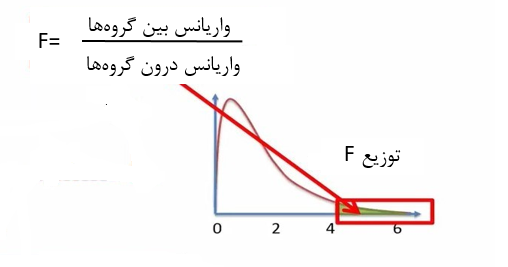
شکل 10. ناحیه بحرانی برای توزیع F در آنالیز واریانس یکطرفه

آزمون‌های تعقیبی (Post hoc tests)

اگر ما فرض صفر (H0) را رد کنیم، نتیجه می‌گیریم که حداقل یک میانگین نسبت به سایر میانگین‌ها متفاوت است. برای اینکه بدانیم کدامیک از میانگین‌ها نسبت به هم تفاوت معنی‌دار دارند از آزمون‌های تعقیبی استفاده می‌کنیم.

فرض کنید برای داده‌های این مثال، فرض صفر را رد کرده‌ایم. بنابراین برای اینکه متوجه شویم کدام گروه میانگین فشار خون بیشتری دارد و همچنین بین کدام گروه‌ها تفاوت معنی‌دار آماری وجود دارد، از آزمون های تعقیبی استفاده می‌کنیم. در این مثال آزمون های تعقیبی کاملاً مشابه با انجام سه آزمون تی مستقل است (شکل 11).

شکل 11. مقایسه میانگین بین گروه‌ها

بر مبنای P-value بدست آمده در شکل 11، می‌توانیم فرض صفر (H0) دوم را رد کنیم. چون مقدار P-value آن از مقدار آلفای 0.05 درصد کوچکتر است. پس نتیجه می‌گیریم که تفاوت معنی‌دار بین فشار خون افراد جوان و سالمند وجود دارد.

اهمیت ANOVA نسبت به چند آزمون تی مستقل

قبل از اتمام این مقاله می‌خواهیم بر اهمیت آنالیز واریانس یکطرفه را نسبت به انجام چند آزمون تی مستقل، تأکید کنیم. وقتی ما سه گروه داریم و سه آزمون تی مستقل انجام می‌دهیم، ریسک خطای نوع اول از 5 درصد به 14 درصد افزایش می‌یابد. در حالیکه ANOVA مانند یک فیلتر عمل میکند. اگر ما در ANOVA نتوانیم فرض صفر را رد کنیم، آزمون دیگری انجام نمی‌دهیم. این موضوع از آزمون میانگین‌هایی که احتمالاً مشابه هستند جلوگیری می‌کند و خطای نوع اول را کاهش می دهد.

در قسمت دوم مقاله ANOVA، محاسبات دقیق آنالیز واریانس یکطرفه را با هم بررسی خواهیم کرد.