آشنایی با آزمون تی زوجی

در این مقاله آزمون تی زوجی (Paired sample t-test) را با مثال بطور کامل بررسی می‌کنیم.

مواردی که با هم در این جلسه بررسی می‌کنیم به شرح زیر است:

• آزمون تی زوجی
• حدود اطمینان
• مفروضات آزمون تی زوجی

کاربرد آزمون تی زوجی

آزمون تی زوجی زمانی استفاده می‌شود که بخواهیم بدانیم تفاوت میانگین بین زوج مشاهدات با عدد صفر تفاوت معنی‌دار دارد یا خیر؟ تفاوت بین آزمون تی مستقل و تی زوجی را هم در ادامه توضیح خواهیم داد. انتخاب بین زوجی یا غیر زوجی بودن آزمون تی (t) بسته به طرح مطالعه دارد.

چه زمانی از آزمون تی زوجی استفاده می‌کنیم؟

فرض کنید می‌خواهیم تأثیر یک نوع دارو را بر کاهش فشار خون 8 فرد بررسی کنیم. برای اینکه آزمون کنیم که آیا دارو تأثیر دارد یا خیر؟ دو گروه ایجاد می‌کنیم و افراد را بطور تصادفی به گروه‌های کنترل و آزمایش اختصاص می‌دهیم (شکل 1).

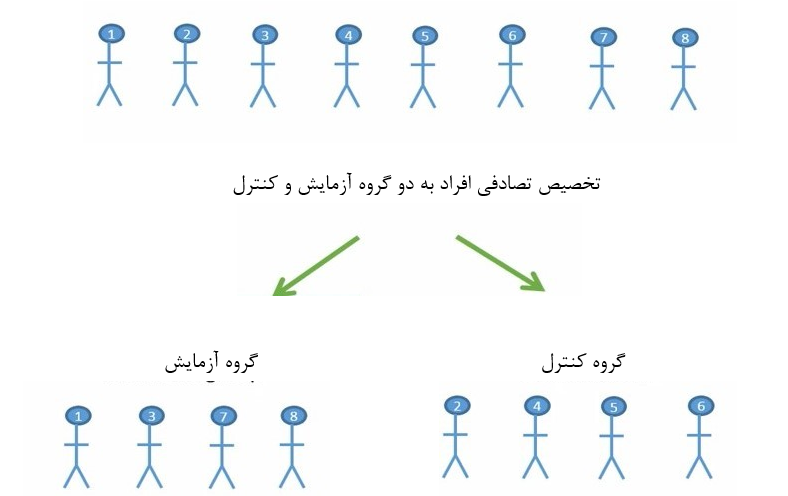
شکل 1. تخصیص تصادفی افراد به دو گروه کنترل و آزمایش

مثلاً افراد 1، 3، 7 و 8 به گروه آزمایش و افراد 2، 3، 4 و 6 به گروه کنترل اختصاص می‌یابند. افراد گروه آزمایش تحت تأثیر دارو قرار می‌گیرند و افراد گروه کنترل دارو نما دریافت می‌کنند. در این آزمایش چون افراد دو گروه کاملاً مستقل هستند، آزمون تی مستقل مناسب است.

اما همین آزمایش را می‌توانیم طوری طراحی کنیم که بتوانیم از آزمون تی زوجی استفاده کنیم. اگر از ابتدا این 8 فرد را بر مبنای فشار خون و جنسیت جفت کنیم، می‌توانیم برای سنجش تأثیر دارو از آزمون تی زوجی استفاده کنیم.

زوج کردن افراد برای انجام آزمون تی زوجی

در شکل 2 ، هشت فرد مثال قبل را بر مبنای جنسیت و فشار خون آورده‌ایم. در این شکل زنان با رنگ قرمز و مردان با رنگ آبی نشان داده شده‌اند.

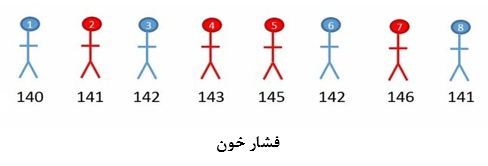
شکل 2. نمایش 8 فرد بر مبنای سن و جنسیت

حالا می‌توانیم افراد را بر مبنای سن و جنسیت جفت کنیم و بعد آزمایش را انجام دهیم. مثلاً می‌توانیم فرد 1 و 8، فرد 2 و 4، فرد 3 و 6 و فرد 5 و 7 را جفت کنیم. جفت کردن بر مبنای تشابه سن و جنسیت انجام می‌شود.

بعد از جفت کردن افراد، یکی از آن‌ها در هر گروه را بطور تصادفی به گروه آزمایش و دیگری را به گروه کنترل اختصاص می‌دهیم (شکل 3).

شکل 3. تخصیص تصادفی یک نفر از افراد هر جفت به گروه آزمایش برای انجام آزمون تی زوجی

بعد از اندازه‌گیری فشار خون، می‌توانیم تفاوت فشار خون در زوج‌ها را محاسبه کنیم. تفاوت فشار خون هر زوج با حذف اثر جنسیت و فشار خون اولیه است بدست می‌آید. لذا با زوج کردن افراد دقت آزمایش را افزایش داده‌ایم.

تقسیم نمونه برای انجام آزمون تی زوجی

مثال دیگر در مورد آزمون تی زوجی، زمانی است که مثلاً یک نمونه خونی از یک فرد گرفته، به دو قسمت تقسیم می‌شود. یک قسمت از این نمونه تحت تیمار دارویی و قسمت دیگر به عنوان کنترل استفاده می شود (شکل 4).

شکل 4. مثال برای آزمون تی زوجی

برای آنالیز این گونه طرح ها نیز از آزمون تی زوجی استفاده می شود. در این طرح تفاوت بین دو نمونه زوجی ناشی از اثر دارو است.

مزیت این گونه طرح‌ها این است که ما تنوع بین سه فرد در ابتدای آزمایش را حذف می‌کنیم. به این ترتیب دقت آزمایش بیشتر می‌شود.

مطالعه قبل-بعد

یک نوع دیگر از مطالعات جفت شده، مطالعات قبل، بعد است. به عنوان مثال، می‌توانیم فشار خون 8 فرد را قبل و بعد از مصرف دارو اندازه‌گیری کنیم (شکل 5). توجه کنید که در این روش تمام افراد ما دارو دریافت می‌کنند و مقادیر قبل به عنوان کنترل استفاده می‌شود.

شکل 5. مطالعه قبل-بعد

محاسبات آزمون تی زوجی

فرض کنید تأثیر یک نوع رژیم غذایی را بر وزن بدن 5 فرد بررسی می‌کنیم. وزن بدن این 5 فرد را قبل و 4 هفته پس از دریافت رژیم غذایی اندازه‌گیری می‌کنیم (شکل 6). اختلاف وزن هر فرد را قبل و بعد از دریافت رژیم غذایی محاسبه و در ستون آخر نوشته‌ایم.

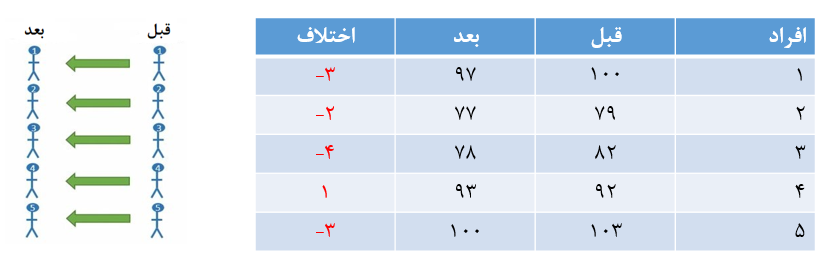
شکل 6. وزن افراد قبل و بعد از دریافت رژیم غذایی

الان می‌توانیم میانگین و انحراف معیار اختلاف‌ها را محاسبه کنیم. محاسبات ریاضی به شرح زیر است:

میانگین تفاوت‌ها در نمونه ما نشان می‌دهد که چهار هفته پس از دریافت رژیم غذایی بطور متوسط 2.2 کیلوگرم کاهش وزن در افراد ایجاد شده است. حال با استفاده از آزمون تی زوجی بررسی می‌کنیم که آیا این کاهش وزن به حدی هست که بتوانیم فرض صفر (H0) را رد کنیم یا خیر؟

در حقیقت ما از آزمون تی زوجی استفاده می‌کنیم تا ببینیم آیا شواهد کافی وجود دارد که فرض صفر را رد کنیم و بگوییم کاهش وزن شانسی رخ نداده است؟

مشخص کردن آزمون فرضیات و سطح معنی‌دار

به این منظور آزمون فرضیات و سطح معنی‌دار (آلفا) تحقیق را مشخص می‌کنیم.

فرض صفر (H0) گزاره‌ای است که بیان می‌کند میانگین‌ تفاوت‌ها با صفر تفاوت معنی‌دار ندارد. در حالی‌که فرض مقابل (H1) بیان می‌کند که میانگین تفاوت‌ها با صفر تفاوت معنی‌دار دارد و در طی 4 هفته مصرف رژیم غذایی تغییر وزن معنی‌دار بوده است.

محاسبه مقدار آماره تی

حالا می‌توانیم مقدار تی را از فرمول زیر محاسبه کنیم. این فرمول دقیقاً همان فرمولی است که برای آزمون تی تک نمونه‌ای استفاده کردیم.

به دلیل اینکه فرض صفر بیان می‌کند که میانگین تفاوت‌های قبل و بعد برابر با صفر است، بنابراین در این فرمول مو-دی را برابر با صفر در نظر می‌گیریم. در اینصورت فرمول آزمون تی زوجی به شکل زیر تغییر می‌یابد.

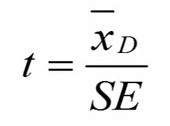
نهایتاً مقدار میانگین تفاوت‌ها و خطای استاندارد تفاوت‌ها را در فرمول جایگذاری می‌کنیم تا آماره تی بدست آید. نهایتاً مقدار تی بدست آمده را روی توزیع تی با درجه آزادی 4 پیدا می‌کنیم (شکل 7).

شکل 7. محاسبه مقدار تی و نمایش آن روی توزیع تی

محاسبه مقدار P-value

حالا با استفاده از یک نرم افزاری آماری می‌توانیم سطح زیر نمودار توزیع تی (سطح هاشور زده شده) برای مقادیر تی بزرگتر از 2.56 و مقادیر تی کوچکتر از 2.56- را پیدا کنیم. این مقدار P-value را به ما نشان می‌دهد (شکل 7).

مقدار P-value در این مثال 0.063 بدست آمد. چون 0.063 کمتر از مقدار آلفای 0.05 است، نمی‌توانیم فرض صفر را رد کنیم. بنابراین نتیجه می‌گیریم که رژیم غذایی بر وزن بدن موثر نبوده است.

دلیل اینکه ما نتوانستیم کاهش وزن 2.2 کیلوگرمی را معنی‌دار اعلام کنیم و فرض صفر را رد کنیم این است که در این مثال نمونه ما بسیار کوچک است. اگر ما همین میانگین کاهش وزن را با تعداد مشاهده بیشتری بدست آوریم، خطای استاندارد کاهش می‌یابد و مقدار آماره تی افزایش می‌یابد. بالا رفتن آماره تی باعث می‌شود که مقدار P-value کاهش پیدا کند و ما بتوانیم فرض صفر را رد کنیم.

محاسبه حدود اطمینان 95 میانگین

حالا می‌توانیم برای میانگین تفاوت‌ها حدود اطمینان 95 درصد محاسبه کنیم. قبلاً در مطلب جداگانه‌ای نحوه محاسبه حدود اطمینان و مفهوم دقیق آن را بررسی کرده‌ایم.

فرمول محاسبه حدود اطمینان به شرح زیر است.

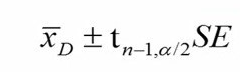
مقدار بحرانی تی برای توزیع تی با درجه آزادی 4 و مقدار آلفای پنج درصد حدوداً برابر با 2.78 است. این مقدار می‌تواند از جداولی موسوم به جداول تی و یا از نرم افزارهای آماری بدست آید.

با جایگذاری میانگین تفاوت‌ها، مقدار تی و خطای استاندارد در فرمول حدود اطمینان را محاسبه می‌کنیم.

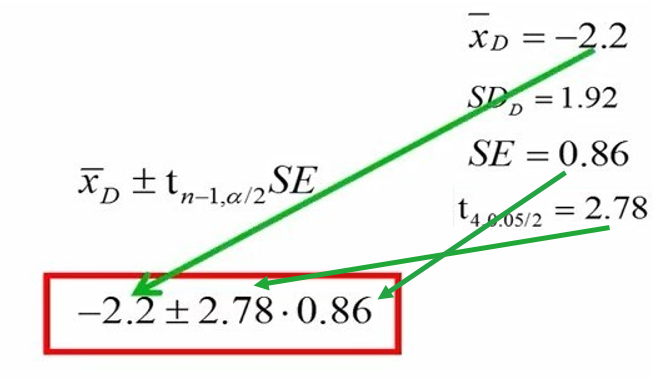
اگر محاسبات ریاضی را انجام دهیم، بازه حدود اطمینان 95 درصد به شرح زیر بدست می‌آید.

در تحقیق ما این بازه در محدوده 4.6- تا 0.2 بدست آمد. بنابراین 95 درصد اطمینان داریم که میانگین جمعیت تفاوت‌های وزن بدن، قبل و بعد از دریافت رژیم غذایی در محدوده 4.6- تا 0.2 قرار می‌گیرد.

توجه کنید که این حدود اطمینان عدد صفر را در بر می‌گیرد. این موضوع نشان می‌هد که برای این حدود اطمینان عدد صفر مقداری کاملاً منطقی است. بنابراین شواهد کافی برای رد فرض H0‌ وجود ندارد.

پیش‌فرض‌ مهم آزمون تی زوجی

مهمترین پیش فرض آزمون تی زوجی این است که مقادیر تفاوت‌ها باید توزیع نرمال داشته باشند. زمانی که نمونه ما کوچک باشد، نمی‌توانیم این مفروض را نادیده بگیریم (شکل 8).

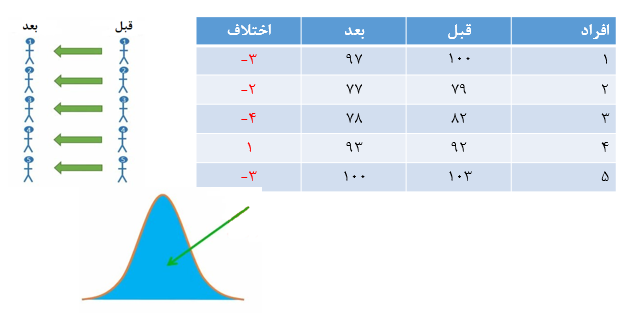
شکل 8. بررسی نرمال بودن توزیع تفاوت‌ها

نکته مهم: برای آزمون تی زوجی، توزیع مقادیر عددی قبل و بعد اصلاً مهم نیست. چون آزمون تی زوجی روی تفاوت‌ها انجام می‌شود، ‌توزیع تفاوت‌ها مهم است. اگر تفاوت‌ها توزیع نرمال نداشت می‌توانیم برای آزمون تأثیر رژیم غذایی از آزمون‌های ناپارامتریک استفاده کنیم.