آشنایی با آزمون نیکویی برازش کای اسکوئر

در این مقاله با آزمون نیکویی برازش کای اسکوئر (Chi-square goodness of fit test) آشنا می‌شویم. همچنین مقایسه‌ای بین آزمون نیکویی برازش کای اسکوئر و آزمون نسبت تک نمونه‌ای (One proportion Z-test) خواهیم داشت.

کاربرد آزمون نیکویی برازش کای اسکوئر

زمانی که بخواهیم نسبت یک نمونه را با یک مقدار مفروض مقایسه کنیم می‌توانیم از آزمون نسبت تک نمونه‌ای یا آزمون نیکویی برازش کای اسکوئر استفاده کنیم.

در این مقاله آزمون نیکویی برازش کای اسکوئر را بررسی می‌کنیم. این آزمون برای سنجش تفاوت فراوانی مشاهده‌ای با توزیع مفروض شناخته شده مورد استفاده قرار می‌گیرد. در نظر داشته باشید که سه نوع آزمون کای اسکوئر وجود دارد که هر کدام را در مقالات جداگانه‌ای بررسی می‌کنیم.

مثال آزمون نیکویی برازش کای اسکوئر

در سال 2015 گروهی از دانشمندان نسبت رایج یک نوع آلرژی را در یک جمعیت بررسی کردند. مطالعه به این نتیجه رسید که 53 درصد از افراد این جمعیت دارای آلرژی بودند. در حالی که 47 درصد سالم و بدون آلرژی بودند.

5 سال بعد، دانشمندان می‌خواستند بدانند که نسبت افراد مبتلا به آلرژی در جمعیت تغییر معنی‌دار یافته است یا خیر؟ اما در این زمان منابع کافی برای بررسی آلرژی تمام جمعیت وجود نداشت. به همین دلیل یک نمونه 100 فردی از جامعه گرفته شد. در این نمونه 49 فرد مبتلا به آلرژی و 51 فرد بدون آلرژی بود (شکل1).

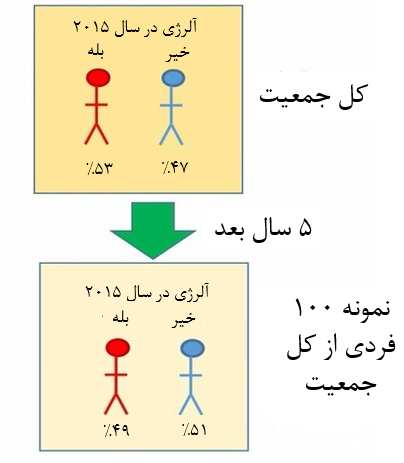
شکل 1. نسبت افراد مبتلا به آلرژی در جمعیت اولیه و 5 سال بعد

آزمون فرضیات

برای بررسی تغییر معنی‌دار نسبت‌ها یا فراوانی‌های افراد مبتلا به آلرژی در جمعیت فعلی نسبت به جمعیت 5 سال قبل، ابتدا آزمون فرضیات را می‌نویسیم.

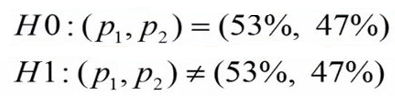
فرض صفر (H0) در این آزمون گزاره‌ای است که بیان می‌کند نسبت‌ها یا فراوانی‌های افراد مبتلا به آلرژی از سال 2015 تغییر معنی‌دار پیدا نکرده است. در حالی که فرض مخالف (H1) بیان می‌کند که نسبت افراد مبتلا به آلرژی در جمعیت تغییر معنی‌دار یافته است.

توجه کنید که در آزمون فرضیات، P1 و P2، به ترتیب نسبت افراد مبتلا به آلرژی و افراد سالم در جمعیت را در سال 2015 نشان می‌دهد. این نسبت‌ها را ما از جمعیت اولیه در سال 2015 داشتیم. حالا بر مبنای داده‌های سال 2020 می‌خواهیم ببینیم که آیا این نسبت‌ها تغییر معنی‌دار کرده‌اند یا خیر؟ به این منظور از آزمون نیکویی برازش کای اسکوئر استفاده می‌کنیم.

محاسبه آماره کای اسکوئر و P-value

فرمول محاسبه آماره کای اسکوئر به شرح زیر است.

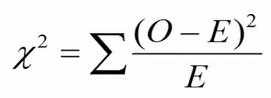
در این فرمول O، فراوانی مشاهده‌ای و E، فراوانی مورد انتظار را نشان می‌دهد.صورت کسر، مربع تفاوت بین فراوانی‌های مورد انتظار است. مخرج کسر فراوانی مشاهده‌ای را نشان می‌دهد.

اطلاعات مثال قبل به شرح زیر است:

حجم نمونه ما در سال 2020، 100 نفر بود. همچنین نسبت افراد مبتلا به آلرژی در سال 2015، مقدار 0.53 و این نسبت در سال 2020، مقدار 0.49 بود. چون آزمون کای اسکوئر بر مبنای فراوانی‌ها عمل می‌کند، باید این نسبت‌ها را به فراوانی تبدیل کنیم.

چون فراوانی‌ها بر مبنای 100 هستند، پس می‌توانیم فراوانی افراد مبتلا به آلرژی را در سال 2015، 53 نفر و در سال 2020، 49 نفر بدانیم. از طرف دیگر فراوانی افراد سالم در سال 2015، 47 نفر و در سال 2020، 51 نفر می‌باشد.

پس ما بر مبنای اطلاعات سال 2015، انتظار داریم که در سال 2020، 53 نفر مبتلا به آلرژی و 47 نفر سالم باشند.

حالا می‌توانیم فراوانی‌های مشاهده شده و مورد انتظار را در فرمول مربوطه‌ قرار دهیم و مقدار کای اسکوئر را محاسبه کنیم.

همانطور که ملاحظه می‌کنید، مقدار آماره کای اسکوئر، 0.64 بدست می‌آید. درجه آزادی این آزمون برابر است با تعداد طبقات متغیر منهای 1. چون دو طبقه داریم، درجه آزادی آزمون ما عدد 1 بدست می‌آید.

برای محاسبه مقدار P-value، باید از توزیع کای اسکوئر با درجه آزادی 1 استفاده کنیم (شکل 2).

شکل 2. سطح زیر نمودار در توزیع کای اسکوئر

ناحیه سمت راست عدد 0.64 در توزیع کای اسکوئر، مقدار P-value است. با استفاده از یک نرم افزار آماری P-value مقدار 0.42بدست می‌آید.

چون P-value از مقدار آلفا (0.05) بزرگتر است، نمی‌توانیم فرض صفر خود را رد کنیم. پس با احتمال خطای پنج درصد، نتیجه می‌گیریم که نسبت افراد مبتلا به آلرژی در طی 5 سال تغییری نکرده است.

مفروض اصلی آزمون نیکویی برازش کای اسکوئر

مفروض اصلی آزمون نیکویی برازش کای اسکوئر این است که فراوانی‌های مورد انتظار در هر طبقه باید حداقل 5 باشد. در مثال مورد بررسی این فراوانی‌ها بالاتر از 5 بود.

مقایسه آزمون نیکویی برازش کای اسکوئر و آزمون نسبت تک نمونه‌ای

مقایسه آزمون نیکویی برازش کای اسکوئر و آزمون نسبت تک نمونه‌ای از دو منظر قابل بررسی است.

آماره‌های آزمون

برای مقایسه آزمون نیکویی برازش کای اسکوئر و آزمون نسبت تک نمونه‌ای، مقدار آماره دو آزمون را با استفاده از فرمول مربوط به دو آزمون محاسبه می‌کنیم.

ملاحظه می‌کنید که در صورت کسر آزمون نسبت تک نمونه‌ای، تفاوت بین نسبت موجود در نمونه و نسبت مفروض وجود دارد. در حالی‌که آزمون کای اسکوئر بر مبنای فراوانی‌های مشاهده‌ای و مورد انتظار، آماره را محاسبه می‌کند. همچنین در آزمون کای‌اسکوئر چون تفاوت فراوانی‌های مشاهده‌ای و مورد انتظار به توان دو می‌رسد، آماره کای اسکوئر همیشه مقداری مثبت دارد. اما Z محاسبه‌ای در آزمون نسبت تک نمونه‌ای می‌تواند مثبت یا منفی باشد.

نکته دیگری که وجود دارد این است که اگر ما مقدار Z (0.8-) را به توان دو برسانیم دقیقاً آماره آزمون کای اسکوئر (0.64) بدست می‌آید.

دو طرفه یا یکطرفه بودن آزمون

به توزیع کای اسکوئر و توزیع Z در شکل 3 زیر دقت کنید:

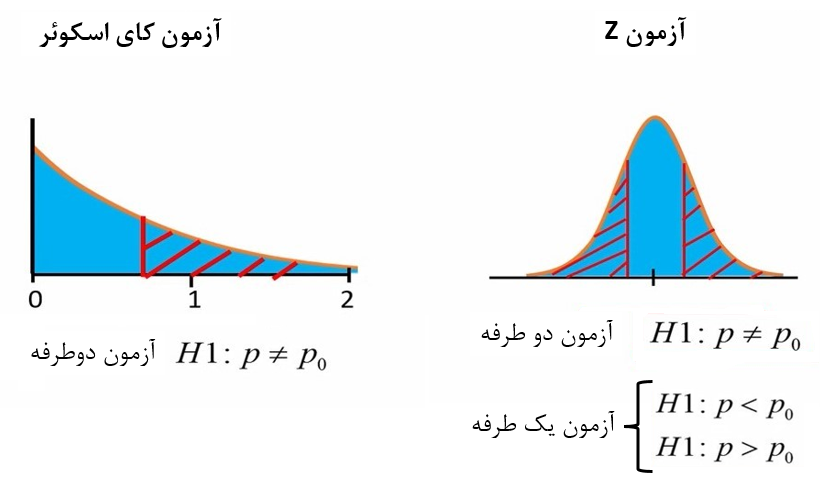
شکل 3. تفاوت توزیع Z و توزیع کای اسکوئر

همانطور که در شکل 4 ملاحظه می‌کنید، توزیع کای اسکوئر متقارن نیست و فقط مقادیر مثبت دارد. به همین دلیل ما فقط فرضیات دو طرفه را می‌توانیم برای این توزیع بنویسیم. در حقیقت ما فقط می‌توانیم آزمون کنیم که آیا تفاوت بین نسبت‌ها وجود دارد یا خیر؟ و نمی‌توانیم بزرگتر یا کوچکتر بودن نسبت نمونه را در مقابل نسبت مفروض آزمون کنیم.

در مقابل، توزیع Z حالت متقارن دارد و می‌تواند مقادیر مثبت یا منفی داشته باشد. در نتیجه برای آزمون نسبت تک نمونه‌ای می‌توانیم فرضیات یکطرفه یا دو طرفه داشته باشیم.

توجه کنید که مقدار P-value برای آزمون کای اسکوئر و آزمون نسبت Z  مشابه است (شکل 4). توزیع کای اسکوئر با درجه آزادی یک را می‌توانیم به عنوان یک توزیع نرمال استاندارد بدون مقادیر منفی در نظر بگیریم.

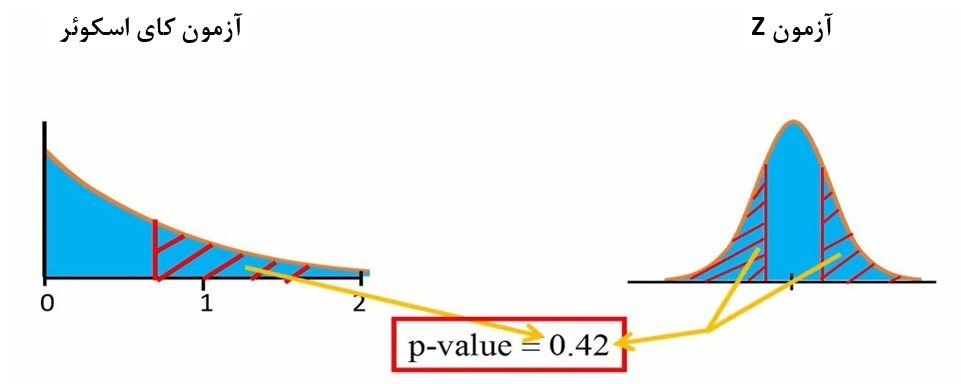
شکل 4. مقدار P-value‌ در آزمون کای اسکوئر و آزمون Z

تبدیل توزیع نرمال به توزیع کای اسکوئر

فرض کنید ما 10000 عدد از توزیع نرمال استاندارد استخراج کنیم و در قالب یک هیستوگرام نمایش دهیم. در اینصورت نموداری مشابه با شکل 6 خواهیم داشت.

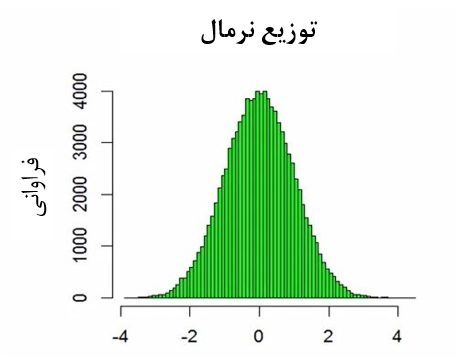
شکل 6. توزیع نرمال

حالا اگر ما همه این 10000 عدد را به توان 2 برسانیم و مجدداً اعداد را در قالب یک هیستوگرام رسم کنیم، شکل توزیع کای اسکوئر را درجه آزادی 1 را خواهیم داشت (شکل 7).

شکل 7. تبدیل توزیع Z به توزیع کای اسکوئر

توجه کنید که چون ما مقادیر را به توان 2 می رسانیم، تمام مقادیر منفی به مقادیر مثبت تبدیل می‌شود. این موضوع شبیه به این است که ما تمام مقادیر منفی نمودار توزیع نرمال را به سمت راست نمودار انتقال دهیم.

همچنین چون مقادیر دو انتهای نمودار توزیع نرمال به توان 2 می‌رسد، انتهای توزیع کای اسکوئر کشیده‌تر می‌شود.

آزمون نیکویی برازش کای‌اسکوئر برای متغیرهای چند طبقه‌ای

بر خلاف آزمون نسبت تک نمونه‌ای، آزمون کای اسکوئر را می‌توانیم زمانی که سه یا بیشتر از سه طبقه داشته باشیم نیز مورد استفاده قرار دهیم.

فرض کنید می‌خواهیم بدانیم که آیا رنگ‌های قرمز، آبی و سبز در یک گل فراوانی مشابه دارند یا خیر؟ در حقیقت می‌خواهیم آزمون کنیم که آیا نسبت‌های برابر بین رنگ‌ها برقرار است؟ (شکل 8).

شکل 8. نسبت مفروض رنگ گل

آزمون فرضیات

فرض صفر (H0) در این آزمایش بیان می‌کند که نسبت رنگ‌های این گل با هم مشابه است. در حالی‌که فرض مخالف نسبت گل‌ها را برابر نمی‌داند.

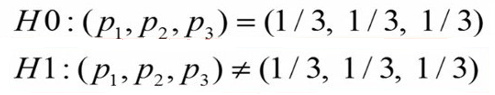
انجام آزمایش

فرض کنید یک نمونه تصادفی شامل 90 گل از مزرعه می‌گیریم و نسبت گل‌ها را در این نمونه محاسبه می‌کنیم. هدف ما این است که تعیین کنیم آیا نسبت رنگ‌ گل‌ها در جمعیت با نسبت مفروض(H0) تفاوت دارد یا خیر؟ در این آزمایش نسبت مفروض ما این است که نسبت رنگ‌ گل‌ها مشابه است.

فراوانی‌های مشاهده‌ای و مورد انتظار

الان باید فراوانی‌ها مشاهده شده هر رنگ را محاسبه کنیم. فرض کنید در این نمونه‌ 90 تایی از رنگ قرمز 27 تا، از رنگ آبی، 36 تا و از رنگ سبز 27 تا مشاهده کرده‌ایم.

در این آزمایش انتظار داریم فراوانی انواع رنگ‌ در گل‌ها مشابه باشد. چون کلاً 90 گل جمع‌آوری کرده‌ایم، فراوانی مورد انتظار برای هر گل 30 عدد است.

محاسبه آماره کای اسکوئر و نتیجه‌گیری

در نهایت فراوانی‌های مشاهده‌ای و مورد انتظار را در فرمول قرار می‌دهیم تا آماره کای اسکوئر بدست آید.

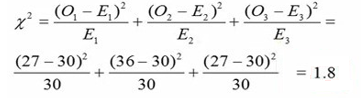
آماره کای اسکوئر در این مثال 1.8 حاصل شد. چون ما سه طبقه داریم، باید توزیع کای اسکوئر با درجه آزادی 2 استفاده کنیم. با استفاده از یک نرم افزار آماری می‌توانیم ناحیه سمت راست عدد 1.8 را محاسبه کنیم. این ناحیه مقدار P-value است (شکل 9).

این آزمایش مقدار P-value عدد 0.41 بدست آمد که بزرگتر از آلفای 0.05 است. بنابراین نتیجه می‌گیریم که نسبت رنگ‌ها در این گل مشابه است و توزیع رنگ‌ها انحراف معنی‌داری از نسبت‌های مشابه که در فرض (H0) مطرح کردیم ندارد.