آشنایی با خطای نوع اول (I) و دوم (II)
در این مقاله با مفهوم خطای نوع اول (I) و نوع دوم (II) آشنا میشویم.
تعریف خطای نوع اول (I) و نوع دوم (II)
زمانی که ما فرض صفر (H0) صحیح را رد میکنیم مرتکب خطای نوع اول (I) شدهایم.
بر عکس، اگر ما فرض صفر (H0) غلط را به اشتباه رد نکنیم، خطای نوع دوم (II) مرتکب شدهایم.
مثال برای خطای نوع اول (I)
در مورد خطای نوع اول (I)، یک پژوهش میتواند دو حالت داشته باشد:
حالت اول
فرض کنید ما دو جمعیت A و B را داریم و قد تمام افراد این دو جمعیت را اندازهگیری کردهایم. یعنی از قبل میدانیم که میانگین قد افراد جمعیت A و B با هم برابر است (شکل 1).
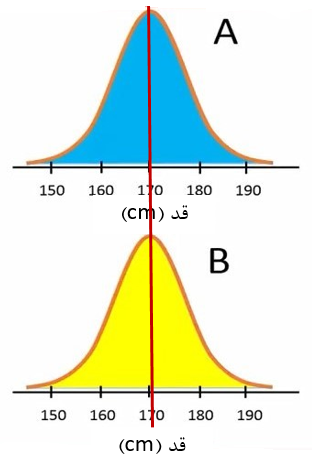
شکل 1. توزیع قد افراد دو جمعیت A و B
محققی در قالب یک پژوهش میخواهد بداند آیا بین قد افراد این دو جمعیت تفاوت معنیدار وجود دارد؟ محقق هیچ اطلاعاتی در مورد قد افراد این دو جمعیت ندارد.
آزمون فرضیات
محقق یک طرح مطالعه طراحی می کند و ابتدا فرضیات صفر (H0) و یک (H1) را بصورت زیر مینویسد:
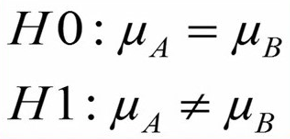
فرض صفر در این مطالعه گزارهای است که میانگین قد افراد را در دو جمعیت برابر میداند. در حالیکه فرض یک (H1) به ما میگوید میانگین قد افراد در دو جمعیت با هم متفاوت است.
توجه کنید که ما الان میدانیم که فرض صفر (H0) ما صحیح است. چون میانگین قد افراد دو جمعیت با هم برابر است. اما محقق هیچ اطلاعاتی در مورد دو جمعیت ندارد.
تعیین حجم نمونه و مقدار سطح معنیدار (آلفا)
محقق ما سطح معنیداری در آزمایش خود را 0.05 در نظر میگیرد و حجم نمونه را برابر با 4 لحاظ میکند.
انجام آزمایش
محقق یک نمونه 4 نفری از جمعیت A و یک نمونه 4 نفری از جمعیت B انتخاب میکند. نهایتاً قد افراد را در دو نمونه اندازهگیری میکند. پس الان یک میانگین قد از نمونه اول و یک میانگین قد از نمونه دوم دارد.
اگرچه دو جمعیت، میانگینهای مشابهی دارند، ولی چون فقط 4 فرد از هر جمعیت انتخاب شده است، طبیعی است که این محقق میانگینهای متفاوتی برای دو جمعیت محاسبه کند. قد افراد و میانگین آنها را روی یک نمودار پراکنش در شکل 2 نمایش دادهایم.
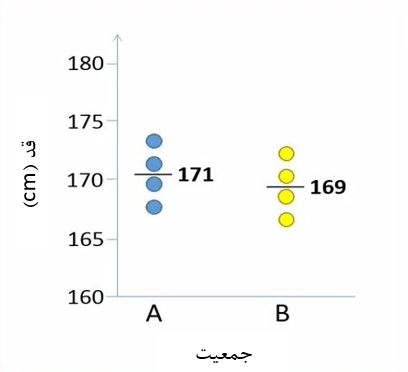
شکل 2. نمودار پراکنش متغیر قد در دو جمعیت A و B
در این مثال میانگین نمونه A مقداری بیشتر از میانگین نمونه B است.
انجام آزمون مناسب و نتیجهگیری
این محقق برای مقایسه دو گروه از آزمون تی مستقل استفاده و مقدار P-value را محاسبه میکند. فرض کنید مقدار P-value عدد 0.2 بدست بیاید. این مقدار بیشتر از سطح معنیدار 0.05 است. پس محقق نتیجه میگیرد که نمیتواند فرض H0 را رد کند و میانگین قد افراد در دو جامعه مشابه است.
چون از قبل میدانیم دو جمعیتی که محقق از آنها نمونهگیری کرده است کاملاً مشابه هستند، پس محقق ما فرض صفر (H0) صحیح را رد نکرده و نتیجه درستی گرفته است. به نتیجهای که محقق ما از این آزمایش گرفته است منفی صحیح (True Negative) میگوییم.
حالت دوم
حالا حالتی را در نظر بگیرید که محقق ما خوش شانس نباشد. یعنی بر مبنای شانس، محقق افرادی را از جمعیت A انتخاب کند که قد آنها بیشتر از میانگین جمعیت باشد. همچنین بر مبنای شانس، افرادی را از جمعیت B انتخاب کند که قد آنها کوتاهتر از میانگین باشد. این قضیه را در شکل 3 نشان دادهایم.

شکل 3. انتخاب افراد خیلی بلند قد یا کوتاه قد در دو جمعیت A و B
مانند دفعه قبل، محقق قد 8 فرد موجود در دو گروه را اندازهگیری و میانگین گروههای A و B را بدست میآورد. برای مقایسه دو گروه نیز از آزمون تی مستقل استفاده میکند. این بار P-value، مقدار 0.006 بدست میآید. چون این مقدار کوچکتر از سطح معنیدار 0.05 است، محقق فرض صفر (H0) را رد میکند و نتیجه میگیرد که تفاوت معنیدار بین میانگینهای قد دو گروه وجود دارد.
حتماً به خاطر دارید که ما از ابتدا میدانیم که این دو جمعیت تفاوتی ندارند. پس چون محقق این بار فرض صفر (H0) صحیح را به غلط رد کرده، مرتکب خطای نوع اول (I) شده است. به نتیجهای که محقق ما از این آزمایش گرفته است مثبت غلط (False Positive) میگوییم. توجه داشته باشید که محقق ما اصلاً نمیداند که مرتکب چنین خطایی شده است.
مثال برای خطای نوع دوم (II)
برای این نوع خطا هم دو حالت ممکن است در آزمایش ما وجود داشته باشد:
حالت اول
فرض کنید، بطور واقعی دو جمعیت A و B از نظر قد تفاوت داشته باشند. به شکل 4 دقت کنید. میانگین قد افراد در جمعیت A، مقدار 170 سانتیمتر و میانگین قد افراد در جمعیت B، مقدار 160 سانتیمتر است.
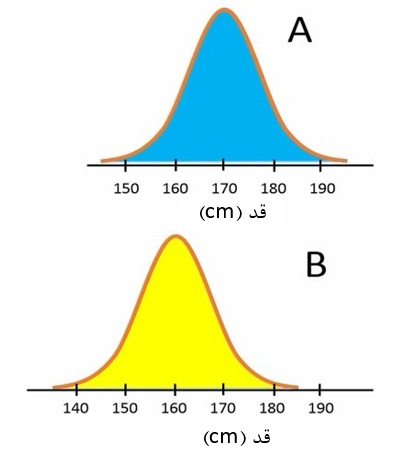
شکل 4. میانگین متفاوت قد در دو جمعیت A و B
در این حالت از قبل میدانیم فرض صفر (H0) غلط و فرض مخالف (H1) صحیح است. چرا که میانگین قد افراد در دو جمعیت A و B تفاوت معنیدار دارند.
محقق میخواهد ببیند آیا بین قد افراد دو جمعیت تفاوت وجود دارد؟
مانند دفعه قبل محقق ما 4 فرد از هر یک از جمعیتها انتخاب میکند و میانگین را برای هر گروه محاسبه میکند (شکل 5). این بار هم از آزمون تی مستقل استفاده میکند تا ببیند دو گروه تفاوت معنیدار دارند یا خیر؟
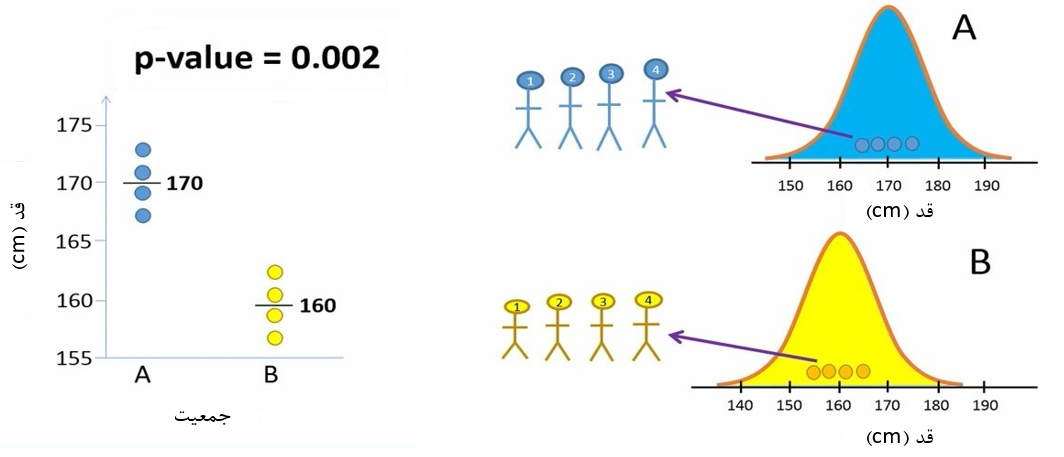
شکل 5. بررسی تفاوت قد دو گروه A و B
در این حالت محقق P-value را 0.002 بدست میآورد. چون P-value کوچکتر از مقدار آلفا (0.05) است، لذا محقق فرض صفر (H0) را رد میکند و نتیجه میگیرد که بین دو جمعیت تفاوت معنیدار وجود دارد.
چون از قبل میدانیم که این دو جمعیت واقعاً تفاوت دارند، پس محقق ما این بار نتیجه صحیح میگیرد. به نتیجهای که محقق ما از این آزمایش گرفته است مثبت صحیح (True Positive) میگوییم.
حالت دوم
حالا حالتی را در نظر بگیرید که محقق ما خوش شانس نباشد. یعنی بر مبنای شانس، محقق افرادی را از جمعیت A انتخاب کند که نسبتاً قد کوتاهی دارند. همچنین بر مبنای شانس، افرادی را از جمعیت B انتخاب کند که قد آنها بلندتر از میانگین است. یعنی با اینکه قد افراد دو جمعیت تفاوت دارد، ولی افرادی از دو جمعیت انتخاب شوند که قد نسبتاً مشابهی دارند. این قضیه را در شکل 6 نشان دادهایم.
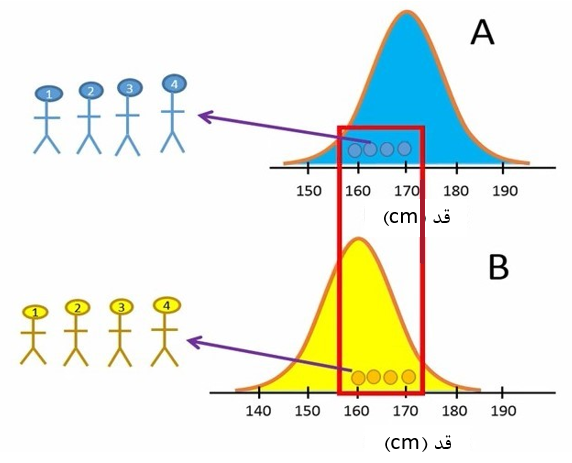
شکل 6. انتخاب افراد کوتاه قد و بلند قد به ترتیب در دو جمعیت A و B
مانند دفعه قبل، محقق قد 8 فرد موجود در دو گروه را اندازهگیری و میانگین قد گروههای A و B را بدست میآورد. به منظور مقایسه میانگین دو گروه از آزمون تی مستقل استفاده میکند. این بار محقق P-value را مقدار 0.7 بدست میآورد. چون این مقدار بزرگتر از سطح معنیدار 0.05 است، محقق فرض صفر (H0) را رد نمیکند و نتیجه میگیرد که تفاوت معنیدار بین میانگینهای قد دو گروه وجود ندارد (شکل 7).

شکل 7. بررسی تفاوت قد دو گروه A و B
حتماً به خاطر دارید که ما از ابتدا میدانیم که این دو جمعیت با هم تفاوت دارند. پس چون محقق این بار فرض صفر (H0) غلط را به اشتباه رد نکرده است، مرتکب خطای نوع دوم (II) شده است. به نتیجهای که محقق ما از این آزمایش گرفته است منفی غلط (False Negative) میگوییم. توجه داشته باشید که محقق ما اصلاً نمیداند که مرتکب چنین خطایی شده است.
جمعبندی مطالب در مورد خطای نوع اول (I) و دوم(II)
الان میتوانیم خطای نوع اول و دوم را بر اساس این جدول بیان کنیم. زمانی که ما یک تحقیق طراحی و بر مبنای آن تصمیمگیری میکنیم 4 نتیجه امکان وقوع دارد که در شکل 8 نشان دادهام.

شکل 8. احتمالات وقوع برای یک نوع آزمایش
در شکل 8 حالاتی که منجر به نتیجه غلط میشود را بصورت پررنگ نشان دادهایم.
مثبت یا منفی بودن نتایج را میتوانیم از مقدار P-value متوجه شویم. اگر P-value کوچکتر از مقدار آلفا (سطح معنیدار) باشد نتیجه مثبت است. اما اگر P-value بزرگتر از آلفا باشد، نتیجه منفی است.
به شکل 8 دقت کنید. مطابق ستون اول جدول، اگر H0 ما صحیح باشد و ما آن را به غلط رد کنیم، نتیجه مثبت غلط حاصل میشود. این نتیجه منجر به خطای نوع اول (I) میشود.
مطابق ستون دوم، اگر H0 ما غلط باشد و به ما آن را به اشتباه رد نکنیم نتیجه منفی غلط بدست آوردهایم. این نتیجه منجر به خطای نوع دوم (II) میشود.
نکته مهم: چون ما هیچ اطلاعاتی از جمعیت اولیه نداریم و تنها اطلاعاتی که داریم از نمونه حاصل شده است، هرگز نمیدانیم که آیا نتایج که از پژوهش گرفتهایم، صحیح یا نادرست است. به همین دلیل است که میگوییم تفاوت معنی دار با سطح خطای 5 درصد وجود دارد. اما هرگز 100 درصد مطمئن نیستیم که تفاوت مشاهده شده، شانسی و بر مبنای نمونه بوده یا تفاوت واقعی بین میانگین دو جمعیت وجود دارد.
مثال موردی در مورد خطای نوع اول (I) و دوم (II)
فرض کنید یک کمپانی دارویی میسازد و میخواهد تأثیر این دارو را در کاهش علائم یک نوع بیماری بررسی کند. به این منظور، کمپانی تعدادی بیمار را به تصادف انتخاب میکند. به نیمی از آنها دارو میدهد. بقیه افراد به عنوان گروه کنترل دارونما دریافت میکنند.
برای این پژوهش دو حالت کلی میتوان در نظر گرفت. یا اینکه بطور واقعی دارو موثر است. یا اینکه دارو تأثیری چندانی در کنترل علائم بیماری ندارد. در ادامه هر دو حالت را بررسی میکنیم:
حالت اول
در این حالت فرض میکنیم که دارو واقعاً موثر نیست.
اگر بر مبنای شانس، افراد مصرف کننده دارو علائم کمتری نسبت به گروه کنترل نشان دهند، کمپانی نتیجه میگیرد که دارو موثر است. در این حالت مرتکب خطای نوع اول (I) شدهایم و نتیجه مثبت غلط است.
اما ممکن است که کمپانی هم بر مبنای تحقیق نتیجه بگیرد که دارو موثر نیست. در این حالت نتیجه منفی صحیح است و هیچ خطایی مرتکب نشدهایم.
حالت دوم
در این حالت فرض میکنیم که دارو واقعاً موثر است.
اگر بر مبنای شانس، افراد مصرف کننده دارو نسبت به گروه کنترل علائم مشابه نشان دهند، کمپانی نتیجه میگیرد که دارو موثر نیست. در این حالت مرتکب خطای نوع دوم (II) شدهایم و نتیجه منفی غلط است.
اما ممکن است که کمپانی هم بر مبنای تحقیق نتیجه بگیرد که دارو موثر است. در این حالت نتیجه مثبت صحیح است و هیچ خطایی مرتکب نشدهایم.

نظرات :