آشنایی با آنالیز واریانس یکطرفه (قسمت دوم)

در این مقاله محاسبات مربوط به آنالیز واریانس یکطرفه (ANOVA) و آزمون‌های تعقیبی را با هم انجام می‌دهیم. قبل از ملاحظه این مقاله لطفا مقاله اول آنالیز واریانس یکطرفه را مطالعه کنید.

از مقاله اول به خاطر دارید که ANOVA، در حقیقت آنالیز واریانس درون و بین گروه‌هاست. قبل از اینکه به محاسبات مربوط به ANOVA بپردازیم، با هم فرمول واریانس را بررسی می‌کنیم.

نحوه محاسبه واریانس

فرض کنید داده‌های فشار خون 4 فرد را داریم. برای محاسبه واریانس نمونه می‌توانیم از فرمول زیر استفاده کنیم (شکل 1).

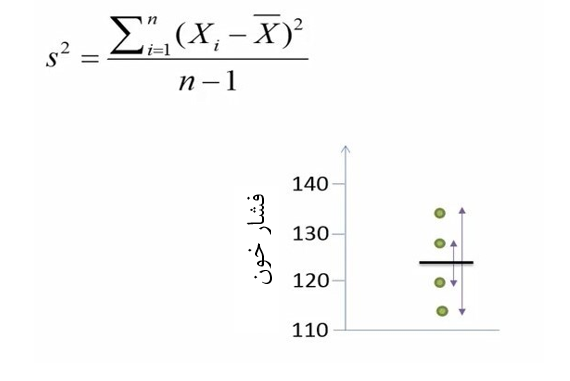
شکل 1. نمایش واریانس فشار خون

صورت کسر فرمول واریانس مجموع مربع تفاوت مشاهدات نسبت به میانگین را نشان می‌دهد. به این معنی که برای بدست آوردن واریانس باید ابتدا تفاوت ارزش هر فرد نسبت به میانگین باید محاسبه شود. این تفاوت‌ها به توان دو برسد و نهایتاً جمع شود. صورت کسر واریانس را مجموع مربعات (مجموع مجذورات) می‌نامیم.

مخرج کسر واریانس، درجه آزادی را نشان می‌دهد. چون ما یک پارامتر از جامعه را برآورد می‌کنیم درجه آزادی ما n-1 می شود. برای آشنایی با درجه آزادی (df) به مقاله مربوطه مراجعه کنید.

حل مثال عددی در مورد آنالیز واریانس یکطرفه (one-way ANOVA)

فرض کنید فشار خون 12 نفر را در سه گروه سنی 4 نفره اندازه‌گیری کرده‌ایم.  چون تعداد افراد مشابهی در همه گروه‌ها وجود دارد طرح آزمایشی ما متعادل است (شکل 2).

شکل 2. اندازه‌گیری فشار خون در سه گروه

نمادهای مربوط به آنالیز واریانس یکطرفه

قبل از انجام محاسبات ANOVA،‌ با نمادهای مربوط به آن آشنا می‌شویم. این نمادها در ادامه ملاحظه می‌کنید.

برای انجام آنالیز واریانس یکطرفه مراحل زیر را انجام می‌دهیم.

• محاسبه میانگین فشار خون هر گروه

ابتدا میانگین فشار خون هر فرد را محاسبه می‌کنیم. میانگین هر گروه را در شکل 3 نشان داده‌ایم.

شکل 3. محاسبه میانگین گروه‌ها

• محاسبه میانگین کل

در مرحله بعد میانگین کل را محاسبه می‌کنیم. میانگین کل را با خط چین قرمز در شکل 4 نشان داده‌ایم.

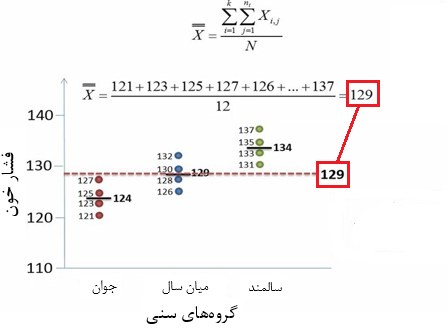
شکل 4. محاسبه میانگین کل

• محاسبه مجموع مربعات داخل گروه‌ها

در این مرحله باید مجموع مربعات داخل گروه‌ها را محاسبه کنیم. این مجموع مربعات خطای آزمایشی یا SSE نامیده می‌شود.

برای محاسبه مجموع مربعات داخل گروه‌ها ابتدا تفاوت هر عدد نسبت به میانگین گروه خودش را محاسبه می‌کنیم. این تفاوت ها را به توان دو می‌رسانیم و با هم جمع می کنیم (شکل 5). در نهایت مجموع مربعات داخل گروه‌ها 60 بدست می‌آید.

شکل 5. محاسبه مجموع مربعات داخل گروه‌ها

• محاسبه مجموع مربعات بین گروه‌ها

در این مرحله باید مجموع مربعات بین گروه‌ها را محاسبه کنیم. این مجموع مربعات SSB یا مجموع مربعات بین نامیده می‌شود.

این کمیت از مجموع ضرب حجم نمونه هر گروه در مربع تفاوت میانگین هر گروه نسبت به میانگین کل حاصل می‌شود (شکل 6). مجموع مربعات بین گروه‌ها 20 بدست می‌آید.

شکل 6. محاسبه مجموع مربعات بین گروه‌ها

• محاسبه مجموع مربعات کل

مجموع مربعات کل را می‌توانیم با جمع مجموع مربعات بین و درون بدست آوریم. در این مثال مجموع مربعات کل 260 بدست می‌آید. روش دیگر محاسبه مجموع مربعات کل جمع کردن مربع تفاوت هر مشاهده نسبت به میانگین کل است شکل (7).

شکل 7. محاسبه مجموع مربعات کل

جایگذاری مجموع مربعات در جدول آنالیز واریانس یکطرفه

با محاسبه مجموع مربعات بین، درون و کل می‌توانیم این اعداد را جدول آنالیز واریانس جایگذاری کنیم (شکل 8).

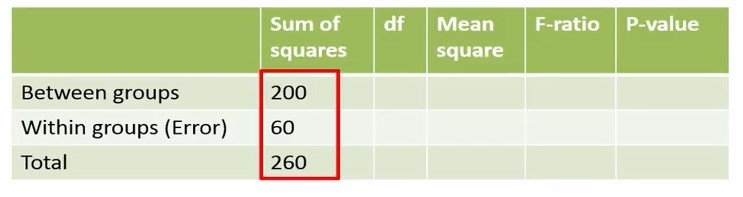
شکل 8. جدول آنالیز واریانس یکطرفه

محاسبه درجه آزادی (df)

ستون سوم در جدول آنالیز واریانس یکطرفه مربوط به درجه آزادی است. درجه آزادی برای منبع تغییر بین گروه‌ها (Between groups)، k-1 است. چون ما سه گروه داریم، درجه آزادی بین گروه‌ها عدد 2 حاصل می شود.

درجه آزادی برای منبع تغییر درون گروه‌ها (within groups) برابر با N-k است. بنابراین برای بدست آوردن درجه آزادی درون گروه‌ها تعداد کل مشاهدات را منهای تعداد گروه‌ها می‌کنیم. برای مثال ما درجه آزادی درون گروه‌ها عدد 9 بدست می‌آید.

درجه آزادی کل برابر با N-1 است. چون 12 مشاهده داریم درجه آزادی کل برابر با 1-12 می‌شود که عدد 11 بدست می‌آید.

اعداد مذکور را در جدول آنالیز واریانس وارد می‌کنیم (شکل 9).

شکل 9. ورود درجه آزادی به جدول آنالیز واریانس

محاسبه میانگین مربعات (Mean of square)

اگر مجموع مربعات هر منبع را تقسیم درجه آزادی کنیم، میانگین مربعات بدست می‌آید. مثلاً برای مجموع مربعات گروه، عدد 200 را باید تقسیم بر 2 کنیم. به این ترتیب مجموع مربعات گروه ما 100 بدست می آید. برای میانگین مربعات بین گروه‌‌ها باید عدد 60 را تقسیم بر 9 کنیم. مجموع مربعات درون گروه‌ها 6.67 بدست می‌آید.

نکته مهم: میانگین مربعات درون هر گروه، در حقیقت یک واریانس ادغام شده (Pooled) از تمام گروه‌هاست که تخمین واریانس عمومی جمعیت را نشان می‌دهد.

میانگین مربعات هر منبع تغییر را وارد جدول می‌کنیم.

شکل 10. وارد کردن میانگین مربعات در جدول آنالیز واریانس

محاسبه نسبت F

از تقسیم میانگین مربعات بین گروه‌ها به درون گروه‌ها می‌توانیم نسبت F را محاسبه کنیم. نسبت F در نمونه ما از تقسیم 100 به 6.67 بدست می‌آید.

این عدد را نیز در جدول آنالیز واریانس وارد می‌کنیم (شکل 11).

شکل 11. وارد کردن نسبت F در جدول آنالیز واریانس

محاسبه مقدار P-value

نهایتاً مقدار P-value را بر مبنای F=15 محاسبه می‌کنیم. این مقدار ناحیه سمت راست توزیع F با درجه آزادی 2 و 9 است (شکل 12).

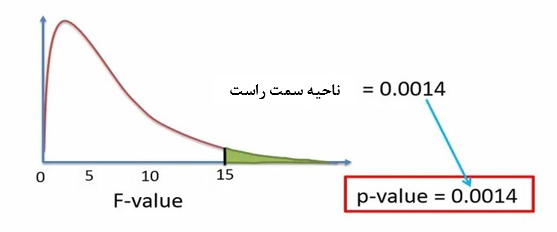
شکل 12. محاسبه مقدار P-value

نهایتاً مقدار P-value را نیز در جدول آنالیز واریانس وارد می‌کنیم.

شکل 13. ورود P-value به جدول آنالیز واریانس

تفسیر نتایج آنالیز واریانس یکطرفه 

چون مقدار P-value کمتر از 0.05 است، نتیجه می‌گیریم که حداقل بین دو گروه سنی، از نظر میانگین فشار خون، تفاوت معنی‌دار وجود دارد. با وجود این نمی‌دانیم کدام میانگین نسبت به میانگین‌های دیگر متفاوت است. ممکن است تفاوت میانگین بین افراد جوان و میانسال، یا افراد جوان و سالمند یا افراد میان سال و سالمند وجود داشته باشد.

برای یافتن اینکه کدام میانگین نسبت به میانگین‌های دیگر متفاوت است، می‌توانیم آزمون‌های تعقیبی انجام دهیم.

آزمون‌‌های تعقیبی در آنالیز واریانس یکطرفه

ساده‌ترین نوع آزمون برای مقایسات چندگانه آزمون حداقل تفاوت معنی‌دار (Least significant difference) یا به اختصار LSD است. این آزمون بر مبنای آزمون‌ تی مستقل بنا نهاده شده است. توجه کنید که این آزمون تنها زمانی استفاده می‌شود که ما از طریق ANOVA فرض صفر (H0) خود را رد کرده باشیم. همچنین تعداد گروه‌های کم داشته باشیم.

فرمول این آزمون به شرح زیر است:

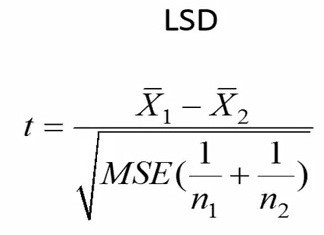
صورت کسر در آزمون LSD، تفاوت بین دو میانگین را نشان می‌دهد. در حالی که در مخرج کسر میانگین مربعات خطا و حجم نمونه‌های دو گروه قرار دارد. توجه داشته باشید که میانگین مربعات خطا واریانس ادغام شده تمام گروه‌هاست. در مثال ما این عدد 6.67 بدست آمد.

در ادامه فرمول دو آزمون تی مستقل و آزمون LSD را آورده‌ام. تنها تفاوت آزمون تی مستقل و آزمون LSD این است که آزمون LSD از واریانس ادغام شده (Pooled) تمام گروه‌های آزمایش استفاده می‌کند. در حالی‌که آزمون تی از واریانس فقط دو گروه استفاده می‌کند. بنابراین اگر برای آنالیز واریانس دو گروه داشته باشیم، نتایج آزمون LSD دقیقاً برابر با نتایج آزمون تی مستقل خواهد بود.

اگر ما همه میانگین‌ها را مقایسه کنیم، مقادیر P-value نشان داده شده در شکل 14 بدست می‌آید. می‌بینیم که تمام میانگین‌ها نسبت به هم تفاوت معنی‌دار دارند. چرا که مقادیر P-value آن‌ها کوچکتر از 0.05 است.

شکل 14. مقادیر P-value در مقایسه میانگین سه گروه با استفاده از آزمون LSD

نکته مهم در استفاده از آزمون های تعقیبی

وقتی ما بیشتر از سه گروه داشته باشیم باید از آزمون‌های تعقیبی استفاده کنیم که مقایسات چندگانه میانگین‌ها را تصحیح (adjust) می‌کنند. دو آزمون بنفرونی و توکی از این آزمون‌ها هستند که در مقالات جداگانه‌ای به آن‌ها می‌پردازیم.