مقایسه آزمون تی تک نمونه ای و حدود اطمینان
در این مقاله آزمون تی تک نمونهای و حدود اطمینان را مقایسه میکنیم.
برای اینکه مطالب این مقاله را بهتر یاد بگیرید، توصیه می کنم مطالب مقالات زیر را ابتدا ببینید.
مثال برای مقایسه آزمون تی تک نمونهای و حدود اطمینان
فرض کنید میخواهیم تأثیر یک نوع رژیم غذایی را بر وزن بدن یکسری افراد بررسی کنیم. به این منظور 6 فرد بطور تصادفی از یک جمعیت انتخاب و رژیم غذایی را به مدت 4 هفته روی آنها آزمون می کنیم. میزان تغییر وزن افراد را در شکل 1 نشان دادهایم.
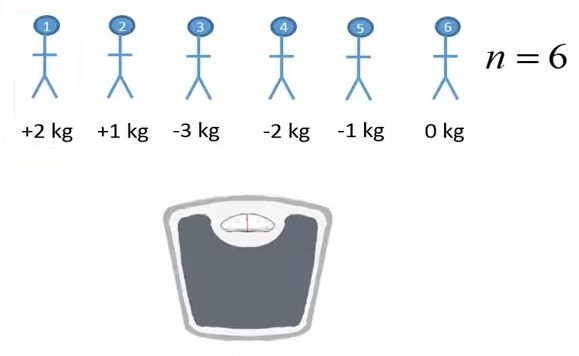
شکل 1. میزان تغییر وزن افراد پس از گذشت چهار هفته از دریافت رژیم غذایی
قبلاً در مقاله مربوط به آزمون تی تک نمونهای اشاره کردیم که میتوانیم میانگین تغییر وزن افراد را با یک عدد پیشفرض یا رفرنس مقایسه کنیم.
همچنین نحوه محاسبه حدود اطمینان برای نمونههای کوچک را در مقاله مربوط به توزیع تی بررسی کردیم. فرمول مربوط به آزمون تی تک نمونهای و همچنین حدود اطمینان در شکل 2 آورده شده است.

شکل 2. فرمول آزمون تی تک نمونهای و حدود اطمینان
با محاسبه میانگین و خطای استاندارد میتوان مقدار آماره تی تک نمونهای و همچنین حدود اطمینان را محاسبه نمود. نحوه محاسبه را در شکل 3 نشان دادهام.

شکل 3. محاسبه آماره تی تک نمونهای و حدود اطمینان
مطابق شکل 3، با جایگذاری کمیتهای میانگین، خطای استاندارد، و مو-صفر مقدار تی برای آزمون تی تک نمونهای 0.655- و حدود اطمینان 95 درصد 2.462- تا 1.462 بدست آمد.
نحوه تفسیر حدود اطمینان و آماره تی تک نمونهای
به شکل 4 دقت کنید. وقتی آماره تی محاسبهای در محدوده اطمینان 95 درصد و بین دو مقدار بحرانی توزیع تی (2.571- تا 2.571) قرار میگیرد، شواهد کافی برای رد فرض H0 نداریم. بنابراین نتیجه میگیریم که رژیم غذایی ما مؤثر نبوده است.
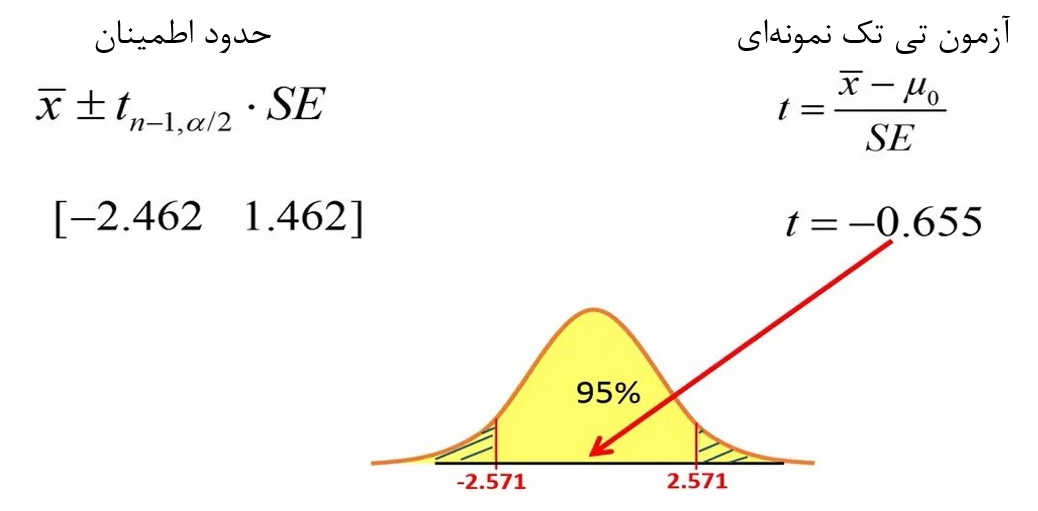
شکل 4. نمایش مقدار تی محاسبهای روی توزیع تی
همین نتیجه را میتوانیم از حدود اطمینان نیز بدست آوریم و فرضیه خودمان را با استفاده از حدود اطمینان رد یا تأیید کنیم.
برای این کار باید چک کنیم که آیا مقدار مو-صفر (مقدار رفرنس) در محدوده اطمینان قرار میگیرد یا خیر؟ (شکل 5).
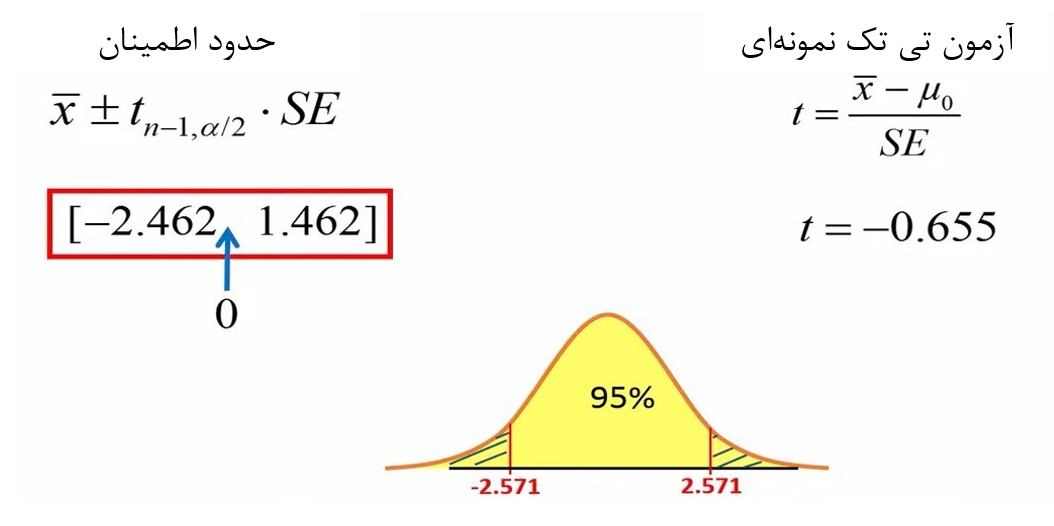
شکل 5. بررسی قرارگیری موصفر در محدوده اطمینان
در مثال ما چون صفر در فاصله اطمینان قرار دارد، نمیتوانیم فرض H0 را رد کنیم. این همان نتیجهای است که از آزمون تی تک نمونهای نیز بدست آوردیم.
شباهت آزمون تی تک نمونهای و حدود اطمینان
در زمان استفاده از حدود اطمینان برای رد یا تأیید فرض صفر، چک میکنیم که مقدار رفرنس درون یا خارج از محدوده اطمینان قرار میگیرد یا خیر؟
اما در زمان استفاده از آزمون تی تک نمونهای، چک می کنیم که آماره تی بین دو مقدار بحرانی تی قرار میگیرد یا خیر؟ (شکل 6).

شکل 6. شباهت آزمون تی تک نمونهای و حدود اطمینان
پس ما هم با حدود اطمینان و هم با استفاده از آزمون تی تک نمونهای میتوانیم فرضیات آزمایش خود را رد یا تأیید نماییم.
مثال موردی (حل با استفاده از آزمون تی تک نمونهای و حدود اطمینان)
فرض کنید میخواهیم بررسی کنیم که افراد مبتلا به یک بیماری خاص نسبت به افراد عادی میزان فشار خونشان تفاوت معنیدار دارد یا خیر؟
در این مثال عدد 120 میلیمتر جیوه مقدار رفرنس (مو-صفر) ما است که میخواهیم میانگین نمونه را با آن مقایسه کنیم. برای این کار ما 8 نفر مبتلا به بیماری را بطور تصادفی انتخاب کرده ایم و فشار خون سیستولیک آن ها را اندازه گیری کرده ایم.
میانگین و خطای استاندارد این 8 نفر به ترتیب 135.5 و 1.4 بدست آمد (شکل 7).
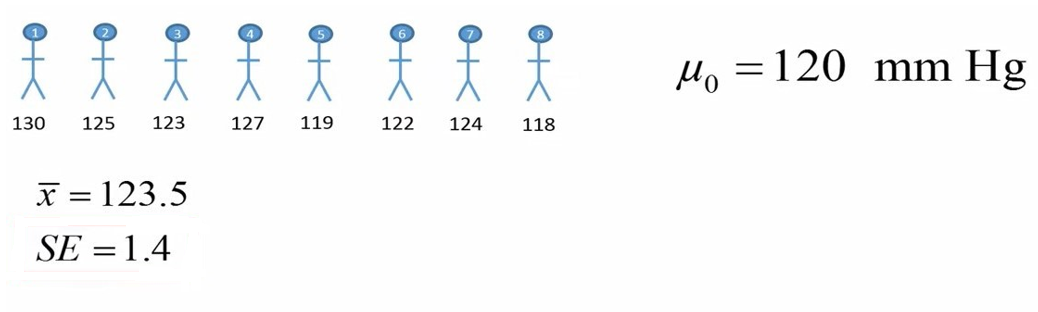
شکل 7. میانگین و خطای استاندارد فشار خون یک نمونه 8 نفری
چون حجم نمونه ما 8 نفر است، باید از توزیع تی با درجه آزادی 7 استفاده کنیم. مقدار بحرانی توزیع تی با درجه آزادی 7 و آلفا 0.05، عدد 2.36 میشود. مقادیر 2.36 و 2.36- را روی توزیع تی با درجه آزادی 7 در شکل 8 نشان دادهام.

شکل 8. مقادیر بحرانی توزیع تی با درجه آزادی 7
الان برای اینکه بدانیم آیا فشار خون افراد دارای بیماری با فشار خون افراد عادی تفاوت دارد یا خیر دو راه داریم. میتوانیم از حدود اطمینان استفاده کنیم. راه دیگر استفاده از آزمون تی تک نمونهای است که در ادامه هر دو روش را بررسی میکنیم.
استفاده از حدود اطمینان برای تأیید یا رد فرض H0
فرمول مربوط به حدود اطمینان به شرح زیر است:

اگر کمیتهای میانگین، خطای استاندارد و مقدار تی بحرانی در سطح خطای 0.05 را در فرمول حدود اطمینان بگذاریم یک محدوده بدست میآید. در مثال ما این محدوده از عدد 120.2 تا 126.8 بدست آمد (شکل 9).
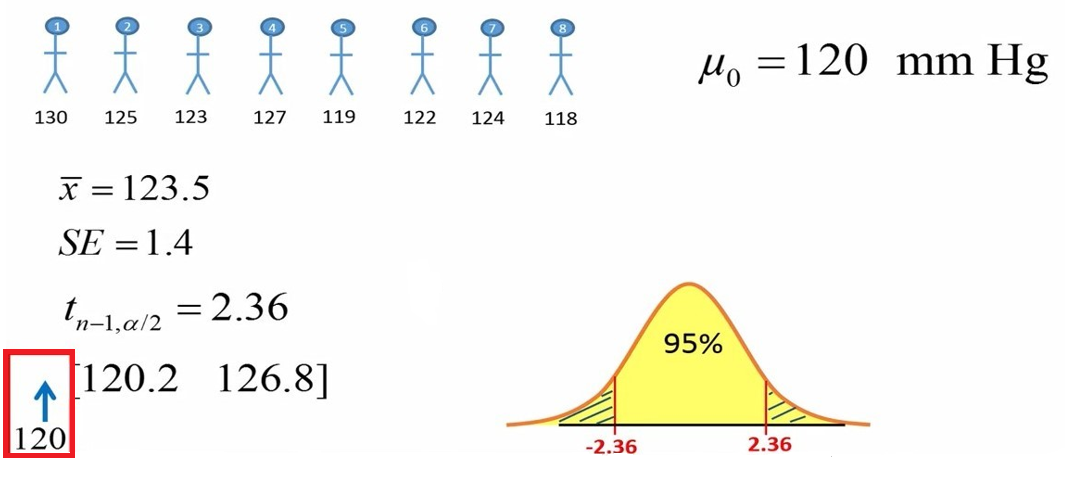
شکل 9. حدود اطمینان 95 % میانگین
حدود اطمینان 95% نشان میدهد که ما 95% اطمینان داریم که میانگین حقیقی جمعیت ما بین دو مقدار 120.2 و 126.8 قرار دارد. می بینیم که حدود اطمینان 95% مقدار 120 را در بر نمیگیرد. پس عدد 120 میلی متر جیوه یک مقدار منطقی برای این محدوده اطمینان نیست. پس نتیجه میگیریم که میانگین فشار خون سیستولیک افراد مبتلا به بیماری بطور معنی داری بیشتر از 120 است. چنانچه عدد 120 در محدوده اطمینان 95 درصد واقع میشد، دیگر نمیتوانستیم فرض H0 را رد کنیم.
استفاده از آزمون تی تک نمونهای برای تأیید یا رد فرض H0
بار دیگر به فرمول آزمون تی تک نمونهای دقت کنید:
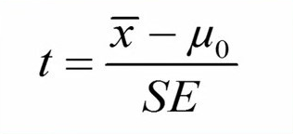
به راحتی میتوانیم با جایگذاری مقادیر، عدد تی را بدست بیاوریم (شکل 10).

شکل 10. محاسبه مقدار تی و نمایش آن روی توزیع تی با درجه آزادی 7
مطابق شکل 10، مقدار تی 2.5 بدست آمد که بزرگتر از مقدار بحرانی 2.36 است. چون مقدار تی در ناحیه بحرانی توزیع تی با درجه آزادی 7 قرار میگیرد، شواهد کافی برای رد فرض H0 داریم. همین نتیجه را از حدود اطمینان نیز بدست آوردیم.
استفاده از P-value برای تأیید یا رد فرض H0
به شکل 11 دقت کنید.

شکل 11. محاسبه مقدار P-value
اگر بر مبنای مقدار تی (2.5) عدد P-value را با استفاده از یک نرم افزار آماری بدست بیاوریم عدد 0.04 حاصل میشود. چون مقدار P-value ما 0.04 است، میتوانیم با اطمینان 95 % نتیجه بگیریم که میانگین جمعیت مبتلا به بیماری با میانگین افراد عادی موجود در جامعه متفاوت است.

نظرات :