آشنایی با آزمون همگنی کای اسکوئر

در این مقاله با آزمون همگنی کای اسکوئر (Chi-square test of homogeneity) آشنا می‌شویم.

تعریف آزمون همگنی کای اسکوئر

برای مقایسه دو یا چند نسبت نمونه‌ای، از آزمون همگنی کای اسکوئر استفاده می‌کنیم. این آزمون فراوانی‌های مشاهده‌ای را نسبت به فراوانی‌های مورد انتظار در جدول متقاطع مقایسه می‌کند.

مثال برای آزمون همگنی کای اسکوئر

فرض کنید می‌خواهیم دو تیمار مختلف را در ارتباط با محافظت از گیاهان در برابر یک پاتوژن مقایسه کنیم. به این منظور 100 گیاه بطور تصادفی به تیمار A و 100 گیاه را به تیمار B اختصاص می‌دهیم. بعد از گذشت دو ماه میزان آلودگی در گیاهان را بررسی می‌کنیم. فرض کنید 25 درصد از گیاهان مربوط به تیمار A آلوده شوند. در حالی‌که از گیاهان تیمار B مقدار 31 درصد مبتلا به بیماری شوند (شکل 1).

شکل 1. درصد گیاهان آلوده در تیمارهای A و B

حالا می‌توانیم اطلاعاتمان را در یک جدول متقاطع خلاصه کنیم. شکل 2، فراوانی و درصد گیاهان آلوده و غیر آلوده را تحت دو تیمار A و B نشان می‌دهد (شکل 2).

شکل 2. جدول متقاطع برای نمایش درصد گیاهان آلوده و غیر آلوده تحت دو تیمار A و B

مطابق شکل 2، به ترتیب 25 و 31درصد از گیاهان تحت دو تیمار A و B آلوده شدند. در جمعیت کلی نیز 28 درصد آلودگی مشاهده می‌شود.

به منظور مقایسه فراوانی گیاهان بیمار و غیر بیمار بین دو جمعیت A و B از آزمون همگنی کای اسکوئر استفاده می‌کنیم.

آزمون فرضیات

برای مقایسه نسبت گیاهان آلوده بین دو تیمار A و B ابتدا آزمون فرضیات را به شرح زیر می‌نویسیم:

فرض صفر (H0) در این آزمون برابری نسبت گیاهان آلوده بین دو تیمار را نشان می‌دهد. در حالی‌که فرض مخالف (H1) بیان می‌کند که دو تیمار A و B با هم تفاوت معنی‌دار دارند.

مشخص کردن سطح معنی‌دار (آلفا)

ما در این آزمایش از سطح 5 درصد برای آزمون استفاده می‌کنیم.

محاسبه آماره کای اسکوئر

فرمول آزمون همگنی کای اسکوئر دقیقاً برابر با فرمول آزمون نیکویی برازش کای اسکوئر است.

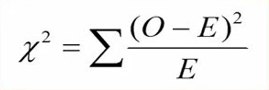
در این فرمول، O، فراوانی مشاهده‌ای و E فراوانی مورد انتظار را نشان می‌دهد.

فراوانی‌های مشاهده‌ای

فراوانی‌های مشاهده‌ای در جدول متقاطع ما کاملاً مشخص هستند (2). به این ترتیب که برای تیمار A، 25 گیاه آلوده و برای تیمار B، 31 گیاه آلوده مشاهده می‌شود.

فراوانی‌های مورد انتظار

برای هر یک از سلول‌های جدول متقاطع باید فراوانی مورد انتظار محاسبه کنیم. مثلاً فراوانی مورد انتظار سلول واقع در ردیف و ستون اول با فرمول زیر محاسبه می‌شود:

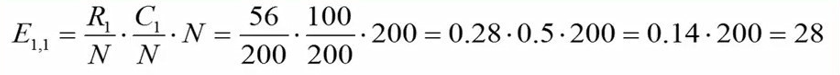
در این فرمول R1، تعداد کل موارد در ردیف اول را نشان می‌دهد. برای مثال R1 برابر با 56 است. حرف N، تعداد کل موارد موجود در آزمایش را نشان می‌دهد. در آزمایش ما بطور کل 200 مورد وجود دارد. حرف C1 تعداد کل موارد در ستون اول را نشان می‌دهد. در تحقیق ما 100 مورد در ستون اول وجود دارد. با عملیات ریاضی می‌توانیم فراوانی مورد انتظار سلول اول (28) را بدست بیاوریم.

حالا با استفاده از موارد موجود در ردیف و ستون‌های هر یک از سلول‌ها می‌توانیم فراوانی‌های مورد انتظار سایر سلول‌های جدول را نیز بدست بیاوریم (شکل 3).

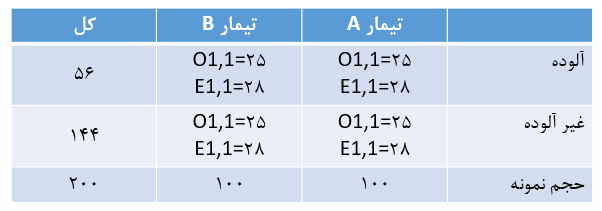
شکل 3. فراوانی‌های مشاهده‌ای و مورد انتظار

محاسبه آماره کای اسکوئر

الان با استفاده از مقادیر مشاهده‌ای و مورد انتظار می‌توانیم آماره کای اسکوئر را محاسبه کنیم.

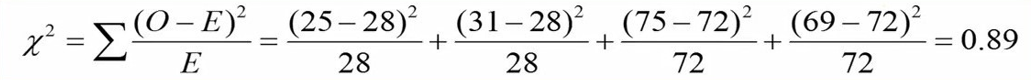
برای هر سلول باید فراوانی مورد انتظار را از فراوانی مشاهده‌ای کم کنیم. عدد حاصل را به توان دو برسانیم و تقسیم بر فراوانی مورد انتظار کنیم. نهایتاً اعداد مربوط به تمام سلول‌ها را با هم جمع کنیم. در آزمایش ما آماره کای اسکوئر را 0.89 آوردیم.

درجه آزادی برای این آزمون برابر است:

df = (R-1)(C-1)

در این فرمول R تعداد ردیف و C تعداد ستون را نشان می‌دهد. چون تعداد ستون و جدول در این مثال 2 است، درجه آزادی ما 1 بدست می‌آید.

پس باید از توزیع کای اسکوئر با درجه آزادی 1 استفاده کنیم.

محاسبه مقدار P-value و نتیجه گیری

می‌توانیم برای محاسبه مقدار P-value از یک نرم افزار آماری استفاده کنیم. ناحیه سمت راست عدد 0.89 مقدار P-value را به ما نشان می‌دهد (شکل 4).

شکل 4. محاسبه مقدار P-value در آزمون کای اسکوئر

در این آزمایش مقدار P-value را 0.34 بدست آورده‌ایم. اگر مقاله مربوط به آزمون مقایسه دو نسبت را مطالعه کرده‌ باشید، می‌دانید که این مقدار دقیقاً همان مقداری است که از آزمون دو نسبت بدست آورده‌ایم.

نکات مهم در مورد آزمون همگنی کای اسکوئر

• هر چه تفاوت بین فراوانی‌های مورد انتظار و مشاهده‌ای بیشتر باشد، آماره کای اسکوئر بزرگتر و احتمال معنی‌داری آزمون بیشتر می‌شود.
• شرط لازم برای انجام آزمون کای اسکوئر این است که تمام خانه‌های جدول حداقل فراوانی مورد انتظار 5 داشته باشند. اگر این شرط برقرار نباشد از آزمون‌های حقیقی مانند آزمون واقعی فیشر (Fisher’s exact test) استفاده می‌کنیم.
• یکی از مزایای آزمون همگنی کای اسکوئر نسبت به آزمون دو نسبت (Z-test) این است که ما می‌توانیم مقایسات را برای بیش دو گروه نیز داشته باشیم.