آشنایی با توزیع تی (T)

در این مفاله با توزیع تی (t-distribution) آشنا می‌شویم. حدود اطمینان را با استفاده از توزیع تی محاسبه می‌کنیم و نکات مهمی در مورد حدود اطمینان خواهیم گفت.

در مقاله مربوط به خطای استاندارد با نحوه محاسبه این کمیت آشنا شدیم. همچنین در مقاله دیگری حدود اطمینان میانگین را زمانی که انحراف معیار جمعیت مشخص بود، محاسبه کردیم. برای آشنایی بهتر با این بخش باید ابتدا این دو مقاله را مطالعه کنید.

اگر از مقاله مربوط به محاسبه حدود اطمینان خاطرتان باشد، ما از عدد 1.96 در فرمول حدود اطمینان استفاده کردیم. اما اگر حجم نمونه ما کم باشد و انحراف معیار جامعه مشخص نباشد نمی‌توانیم از عدد 1.96 در فرمول محاسبه حدود اطمینان استفاده کنیم.

مثال برای درک اهمیت توزیع تی

محاسبه حدود اطمینان با فرض معلوم بودن انحراف استاندارد جمعیت

فرض کنید یک جامعه داریم که شامل قد افراد است. برای تخمین میانگین قد افراد این جمعیت یک نمونه تصادفی 4 فردی از جمعیت می‌گیریم. میانگین قد این 4 فرد را محاسبه می‌کنیم. مثلاً این میانگین برای نمونه ما 166 بدست آمد. چون انحراف استاندارد جمعیت و حجم نمونه را می‌دانیم به راحتی می‌توانیم خطای استاندارد میانگین را محاسبه کنیم. در مثال ما خطای استاندارد 5 بدست آمد. در نهایت ما حدود اطمینان 95 درصد میانگین را با استفاده از ضرب عدد 1.96 در خطای استاندارد بدست می‌آوریم.  این حدود برای مثال ما 156.2 تا 175.8 بدست آمد. تمام موارد را در شکل 1 نشان داده‌ایم.

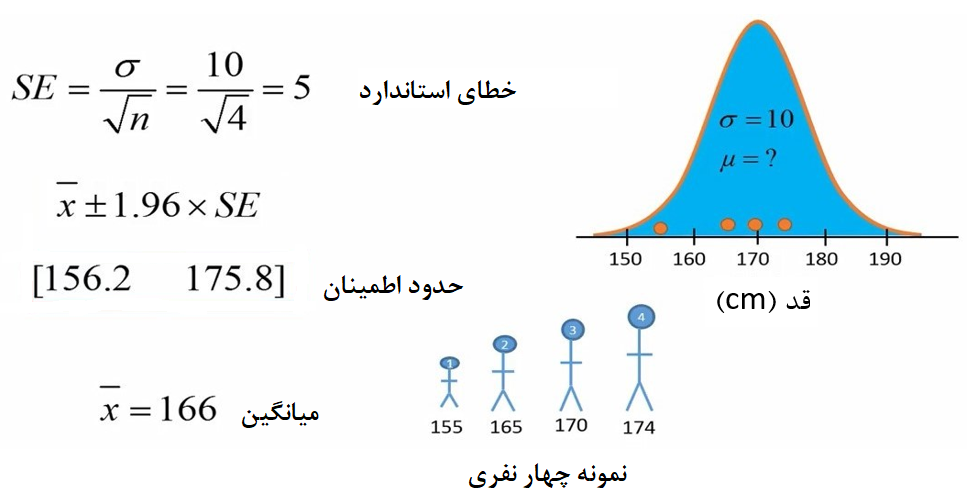
شکل 1. محاسبه میانگین، خطای استاندارد و حدود اطمینان برای جمعیت دارای انحراف معیار معلوم

حالا فرض کنید یک نمونه دیگر از جمعیت می‌گیریم. دقیقاً مانند نمونه قبل، میانگین، خطای استاندارد و حدود اطمینان را برای این نمونه هم محاسبه می‌کنیم (شکل 2). توجه کنید چون در نمونه دوم به تصادف افراد دیگری قرار می‌گیرند، پس میانگین نمونه ما متفاوت خواهد بود. اما چون انحراف معیار جمعیت ما مشخص است، مقدار خطای استاندارد دقیقاً مشابه با نمونه قبل است.

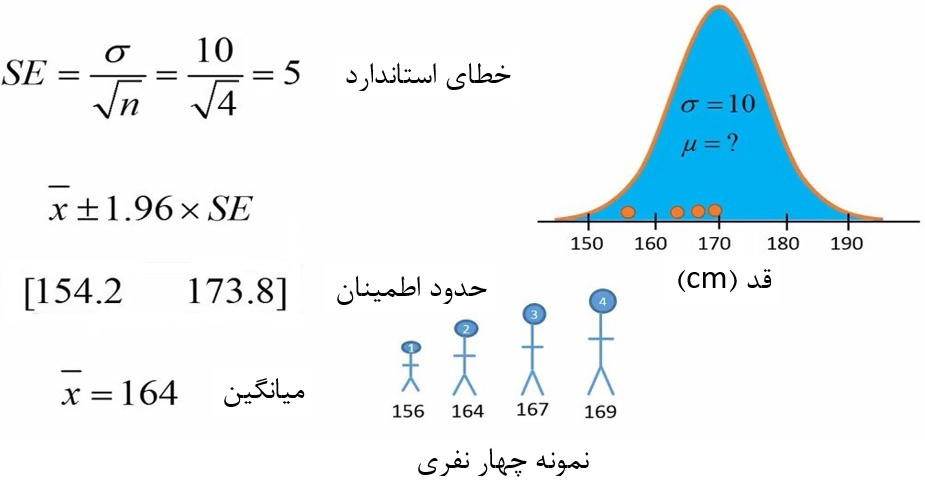
شکل 2. محاسبه میانگین، خطای استاندارد و حدود اطمینان نمونه دوم برای جمعیت دارای انحراف معیار معلوم

حالا فرض کنید ما فرایند نمونه‌گیری را 20 بار تکرار کنیم، در اینصورت 20 میانگین مختلف و 20 حدود اطمینان خواهیم داشت. اگر روی یک دیاگرام، میانگین واقعی جمعیت را به همراه حدودهای اطمینان نشان دهیم شکل 3 را خواهیم داشت.

شکل 3. تخمین میانگین جمعیت و حدود اطمینان با استفاده از 20 نمونه

نکات مهم در مورد حدود اطمینان

بر مبنای حدود اطمینان 95 درصد، می‌توانیم بگوییم، 95 درصد اطمینان داریم که میانگین حقیقی جمعیت در حدود اطمینان ما قرار می‌گیرد. پس انتظار داریم که از 20 حدود اطمینان محاسبه شده یکی از آ‌ن‌ها شامل میانگین حقیقی جمعیت باشد. اگر به شکل 3 دقت کنید، یک حدود اطمینان از 20 حدود اطمینان، شامل میانگین حقیقی جمعیت نیست که با مستطیل قرمز نشان داده‌ام. نکته‌ای که وجود دارد این است که ما هرگز نمیدانیم که حدود اطمینان ما شامل میانگین حقیقی جمعیت هست یا خیر؟ اما می‌توانیم 95 درصد اطمینان داشته باشیم.

با دقت بیشتر روی حدود اطمینان‌‌ها در می‌یابیم که این حدود اطمینان‌ها فواصل مشابهی دارند. چرا که خطای استاندارد ما از انحراف معیار شناخته شده جمعیت (10) محاسبه شده است. همچنین تمام نمونه‌ها حجم مشابهی دارند. تنها تفاوت حدود اطمینان‌ها موقعیت‌ آن‌هاست که بر مبنای میانگین هر نمونه تصادفی متفاوت است.

اما در مطالعات واقعی اغلب ما انحراف معیار جمعیت را نمی‌دانیم! بنابراین ما باید انحراف معیار را بر مبنای اطلاعات نمونه تخمین بزنیم.

حدود اطمینان در مطالعات واقعی

در مطالعات واقعی عموماً ما انحراف معیار جمعیت را نمی‌دانیم. بنابراین باید انحراف معیار جمعیت را بر مبنای اطلاعات نمونه تخمین بزنیم.

بطور خلاصه، برای پژوهش‌‌مان سه حالت می‌تواند وجود داشته باشد. برای این سه حالت سه فرمول مختلف در زیر آورده شده است.

• اینکه ما انحراف معیار جمعیت را بدانیم. در اینصورت میتوانیم حدود اطمینان 95% میانگین را با استفاده از فرمول سمت چپ محاسبه کنیم. در این فرمول عدد 1.96 را استفاده می‌کنیم.
•  اگر ما انحراف معیار جمعیت را ندانیم. در صورتی که حجم نمونه بالاتر از 100 باشد، باز هم از عدد 1.96 برای بدست آوردن حدود اطمینان 95% استفاده می‌کنیم. اما این بار انحراف معیار جمعیت را از روی نمونه تخمین می‌زنیم.
• اگر انحراف معیار جمعیت را بر مبنای یک نمونه کوچک تخمین بزنیم، دیگر نمی‌توانیم از عدد 1.96 برای محاسبه حدود اطمینان 95% استفاده کنیم. بلکه باید از عدد بزرگتری استفاده کنیم که این عدد را از توزیع تی بدست می‌آوریم.

دلیل اینکه باید از مقادیر بزرگتر استفاده کنیم را در ادامه با مثال توضیح خواهیم داد.

نحوه محاسبه حدود اطمینان 95% برای جمعیت‌های بدون انحراف معیار معلوم

فرض کنید در مثال قبل ما انحراف معیار واقعی جمعیت را نمی‌دانیم. پس باید این انحراف معیار را از طریق نمونه تخمین بزنیم. توجه کنید که این بار، چون هر نمونه ما از جامعه بطور تصادفی اخذ می‌شود، ‌انحراف معیار بر مبنای نمونه متفاوت خواهد بود. در صورتی که در مثال قبل انحراف معیار را بصورت ثابت عدد 10 در نظر می‌گرفتیم.

اگر با توجه به نمونه میانگین و حدود اطمینان را محاسبه کنیم شکل 4 را خواهیم داشت.

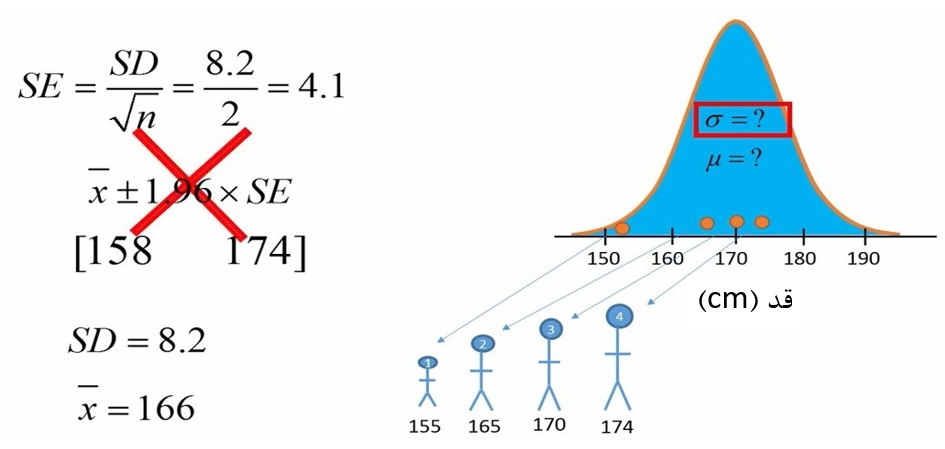
شکل 4. محاسبه میانگین و حدود اطمینان برای جمعیت بدون انحراف معیار معلوم

توجه کنید که این بار خطای استاندارد ما به جای عدد 5، عدد 4.1 بدست آمده است. این موضوع به این دلیل است که در فرمول خطای استاندارد از انحراف استاندارد نمونه استفاده شده است. اما برای بدست آوردن حدود اطمینان، عدد 1.96 مناسب نیست. بلکه باید از عدد متفاوت دیگری که از توزیع تی بدست می‌آوریم استفاده کنیم.

حال برای محاسبه حدود اطمینان دیگر نمی‌توانیم از عدد 1.96 استفاده کنیم و باید عدد مربوطه را از توزیع تی بدست بیاوریم.

مفهوم توزیع تی

توزیع شکل 6، توزیع تی با درجه آزادی 3 است. این توزیع شکلی شبیه به توزیع نرمال دارد. یعنی زنگوله‌ای و متقارن است. اما این توزیع نسبت به توزیع نرمال قله کوتاه‌تری دارد و از کناره‌ها نیز عریض‌تر است. به همین دلیل مقادیری که برای محاسبه حدود اطمینان 95 درصد در توزیع تی استفاده می‌کنیم نسبت به توزیع نرمال بیشتر است.

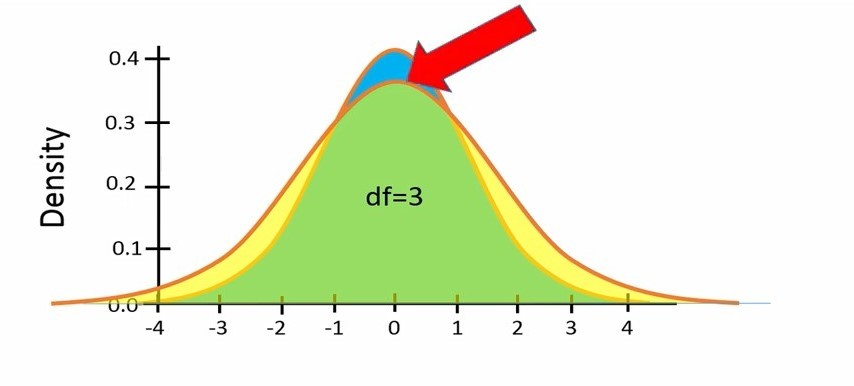
شکل 5. توزیع تی با درجه آزادی 3

در توزیع نرمال استاندارد برای پوشش 95 درصد سطح زیر نمودار، از دو عدد 1.96+ و 1.96- استفاده می‌کردیم. اما در توزیع تی با درجه آزادی 3 برای پوشش 95 % از دو عدد 3.18+ و 3.18- استفاده می‌کنیم. این اعداد برای توزیع‌های تی با درجه‌های مختلف آزادی متفاوت است (شکل 7). پس برای محاسبه حدود اطمینان زمانی که حجم نمونه ما 4 است باید از دو عدد تی 3.18 و 3.18- استفاده کنیم.

شکل 6. اعداد بحرانی توزیع تی با درجه آزادی 3 و مقایسه آن‌ها با توزیع نرمال

تأثیر حجم نمونه در حدود اطمینان

زمانی که حجم نمونه ما 4 است، محدوده حدود اطمینان‌ها نسبتاً بزرگ است (شکل 7). چون ما برای محاسبه حدود اطمینان، خطای استاندارد را در یک عدد بزرگ مثلاً 3.18 ضرب می‌کنیم.

اما زمانی که حجم نمونه‌ را افزایش می‌دهیم، محدوده حدود اطمینان‌ها باریک‌تر می‌شود. چون ما خطای استاندارد را در عدد کوچکتری ضرب می‌کنیم. در شکل زیر محدوده حدود اطمینان در 20 نمونه 4 نفری و در 20 نمونه 10 نفری را مشاهده می‌کنید. به وضوح باریک‌تر بودن محدوده اطمینان در نمونه‌های 10 نفری قابل مشاهده است. هر چه محدوده باریکتر باشد، نشان می‌دهد که ما به میانگین تخمینی اعتماد بیشتری داریم.

شکل 7. مقایسه حدود اطمینان‌ در نمونه‌های با حجم 4 و 10

تأثیر حجم نمونه در توزیع تی

هر چه اعضای نمونه افزایش می‌یابد، توزیع تی مشابهت بیشتری به توزیع نرمال پیدا می‌کند. توزیع تی با درجه‌های مختلف آزادی را در شکل‌های 8 تا 10 مشاهده می‌کنید.

شکل 8. مقایسه توزیع تی با درجه آزادی 3 و توزیع نرمال

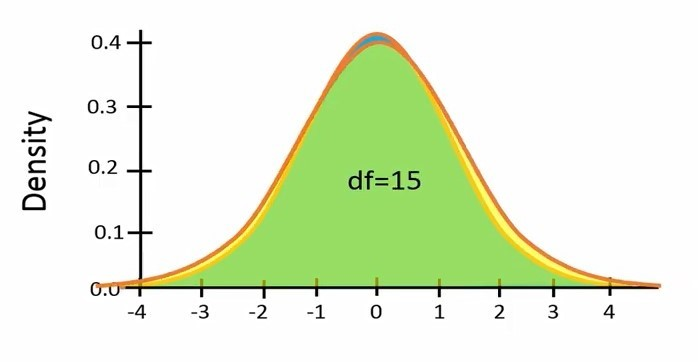
شکل 9. مقایسه توزیع تی با درجه آزادی 15 و توزیع نرمال

شکل 10. توزیع تی با درجه آزادی 100 و توزیع نرمال

همانطور که ملاحظه می‌کنید، برای درجه آزادی 100 توزیع تی تقریباً مشابه با توزیع نرمال است. پس هر چه حجم نمونه افزایش یابد، ‌درجه آزادی افزایش و توزیع تی به توزیع نرمال نزدیک می‌شود. مطابق شکل 12، برای توزیع تی با درجه‌های مختلف آزادی، اعداد متفاوتی نیاز است تا بتوانیم 95 % از توزیع تی را پوشش دهیم. توجه کنید که برای درجه آزادی 100، مقادیر تی برای پوشش 95 % توزیع تی، 1.98- و 1.98+ است. توجه کنید که مقدار 1.98 خیلی نزدیک به 1.96 است که برای توزیع نرمال استاندارد کاربرد دارد. به همین خاطر است که برای محاسبه حدود اطمینان 95 درصد زمانی که حجم نمونه بالای 100 است، از عدد 1.96 استفاده می کنیم.

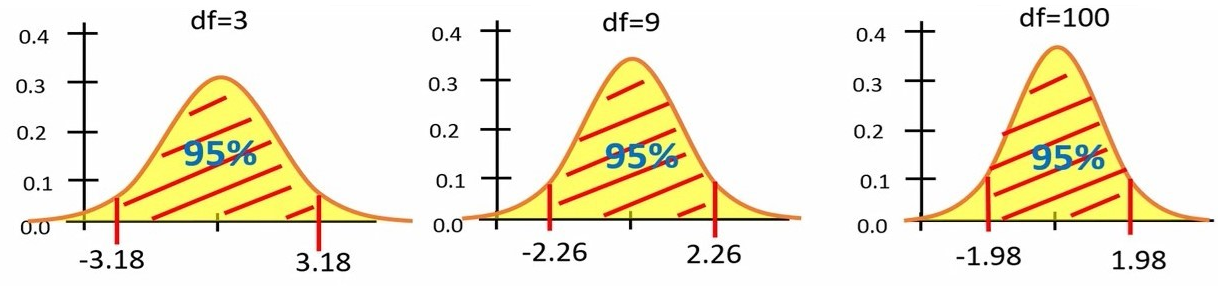
شکل 11. توزیع تی با درجه‌های آزادی مختلف

نحوه محاسبه مقدار تی

برای محاسبه مقدار تی می‌توانیم از جداولی به نام جداول توزیع تی استفاده کنیم. اما این روش قدیمی است و کمتر استفاده می‌شود. در حال حاضر با استفاده از نرم افزار‌های آماری می‌توانیم مقادیر تی را داشته باشیم. به خاطر داشته باشید که بسیاری از نرم افزارهای آماری قادرند بطور اتوماتیک مقادیر مناسب تی را برای مبنای حجم نمونه محاسبه کنند.