انحراف استاندارد به زبان ساده: راهنمای تصویری برای درک پراکندگی داده‌ها

آیا تا به حال به این فکر کرده‌اید که چرا نمرات دانش‌آموزان یک کلاس همیشه یکسان نیست؟ یا چرا قد افراد یک جامعه متفاوت است؟ پاسخ این سوال‌ها در مفهومی به نام “انحراف استاندارد” نهفته است.

انحراف استاندارد، مثل یک متر، به ما کمک می‌کند تا پراکندگی داده‌ها را اندازه‌گیری کنیم. به زبان ساده‌تر، انحراف استاندارد نشان می‌دهد که به طور متوسط، داده‌ها چقدر از میانگین فاصله دارند. هرچه انحراف استاندارد بیشتر باشد، به این معنی است که داده‌ها پراکنده‌تر هستند و برعکس.

چرا دانستن انحراف استاندارد مهم است؟

• تفسیر نتایج تحقیقات: با دانستن انحراف استاندارد، می‌توانیم نتایج تحقیقات را بهتر تفسیر کنیم. مثلاً، اگر دو گروه از دانش‌آموزان را با هم مقایسه کنیم، می‌توانیم بگوییم که آیا تفاوت نمرات آن‌ها معنی‌دار است یا خیر.
• کنترل کیفیت: در صنایع مختلف، از انحراف استاندارد برای کنترل کیفیت محصولات استفاده می‌شود. مثلاً، اگر انحراف استاندارد وزن یک محصول خیلی زیاد باشد، به این معنی است که کیفیت محصول یکنواخت نیست.
• پیش‌بینی آینده: با استفاده از انحراف استاندارد می‌توانیم پیش‌بینی کنیم که داده‌های آینده چگونه خواهند بود. مثلاً، اگر انحراف استاندارد بازده یک سهام زیاد باشد، به این معنی است که سهام نوسانات زیادی دارد و سرمایه‌گذاری در آن ریسک بیشتری دارد.

در این مقاله، شما یاد خواهید گرفت:

• انحراف استاندارد چیست و چرا مهم است؟
• چگونه انحراف استاندارد را محاسبه کنیم؟
• چه تفاوتی بین انحراف استاندارد و واریانس وجود دارد؟
• چگونه انحراف استاندارد را تفسیر کنیم؟
• کاربردهای انحراف استاندارد

اگر می‌خواهید به دنیای آمار و تحلیل داده‌ها قدم بگذارید و داده‌های خود را بهتر درک کنید، این مقاله را از دست ندهید. با ما همراه باشید تا با استفاده از مثال‌های ساده و نمودارهای جذاب، مفهوم انحراف استاندارد را به طور کامل فرا بگیرید.

قبلاً در طی مقاله‌ای معیارهای دیگری از پراکندگی داده‌ها را شامل محدوده‌ داده‌ها، دامنه میان چارکی و نمودار باکس پلات را بررسی کرده‌ایم که برای یادگیری این معیارهای میتوانید مقاله مذکور را مطالعه کنید.

انحراف استاندارد

انحراف استاندارد با استفاده از فرمول زیر بدست می آید.

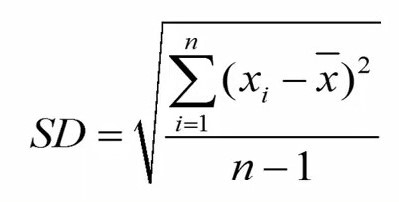
اجزای فرمول به شرح زیر است:

n، حجم نمونه

Xi، ارزش مشاهده X در جایگاه i

ایکس-بار: میانگین مقادیر

مثال

فرض کنید ارتفاع سه گیاه را اندازه‌گیری کرده‌اید. ارتفاع این سه گیاه به ترتیب 3، 4 و 6 سانتیمتر است (شکل 1).

شکل 1. نمایش ارتفاع گیاه روی نمودار

برای محاسبه انحراف استاندارد باید مراحل زیر را انجام دهیم:

• محاسبه میانگین

میانگین از جمع مقادیر تقسیم بر تعداد آن‌ها حاصل می‌شود. در مثال ما میانگین عدد 4 بدست آمد.

• محاسبه مجموع مربعات

حالا باید تفاوت هر یک از نقاط را نسبت به میانگین محاسبه و به توان دو برسانیم. در شکل 2 فاصله نقاط نسبت به میانگین را نشان داده‌ایم. همچنین فاصله هر نقطه نسبت به میانگین را ابتدا محاسبه و سپس به توان دو رساندیم. نهایتاً مجموع مجذور تفاوت‌ها از میانگین را محاسبه کردیم که عدد 8 بدست آمد. عدد 8 در صورت کسر واریانس قرار می‌گیرد.

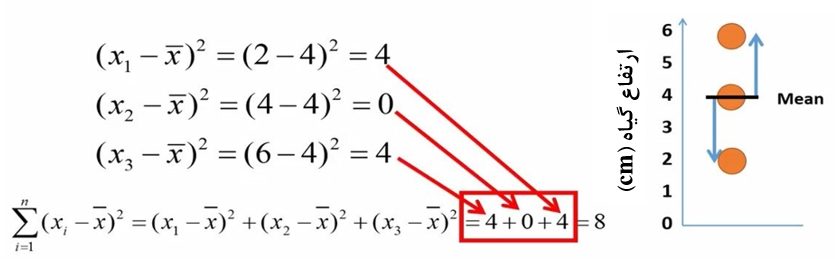
شکل 2. نحوه محاسبه مجموع مربعات

• محاسبه انحراف استاندارد

در نهایت عدد 8 را تقسیم بر درجه آزادی می‌کنیم و از آن جذر می‌گیریم تا واریانس بدست آید. نهایتاً از واریانس جذر می‌گیریم.

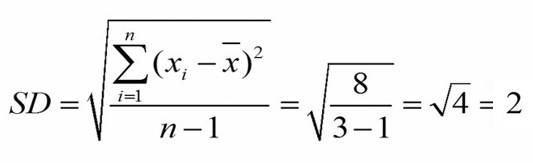
میانگین همراه با انحراف استاندارد

اگر انحراف استاندارد را به علاوه-منهای میانگین کنیم، یک بازه بدست می‌آید. برای مثال ما می‌توانیم میانگین و انحراف استاندارد را به شکل زیر بنویسیم.

اگر عدد 4 را یکبار با عدد 2 جمع کنیم و بار دیگر 2 را از 4 کم کنیم یک بازه حاصل می‌شود. این بازه را می‌توان روی یک نمودار میله‌ای مانند شکل 3 نشان داد.

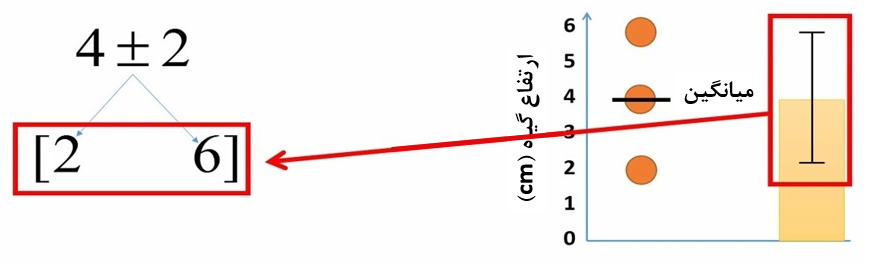
شکل 3. نمایش میانگین و انحراف معیار روی نمودار ستونی

اگر توزیع داده‌های ما نرمال باشد، می‌توانیم این بازه را به این صورت تفسیر کنیم که حدود 68 درصد از داده‌ها در محدوده یک انحراف استاندارد از میانگین قرار می‌گیرند. چون در این مثال 3 عدد بیشتر نداشتیم، تصور این موضوع کمی مشکل است. اجازه دهید با یک مثال دیگر مطلب را بهتر شرح بدهیم.

مثال

تصور کنید ارتفاع 70 گیاه را اندازه گیری کرده‌ و روی یک نمودار ستونی نمایش داده‌ایم (شکل 4).

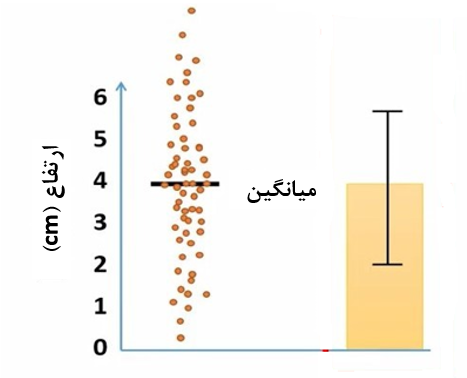
شکل 4. نمایش میانگین و انحراف معیار روی نمودار ستونی

الان میتوانیم ارور بار را به این شکل تفسیر کنیم که حدود 68 درصد از اعداد بین محدوده ارور بار قرار می گیرند. مقدار 68% را از خصوصیات توزیع نرمال گرفته‌ایم. توزیع نرمال را در جلسه جداگانه‌ای بطور مفصل بررسی کرده‌ایم.

واریانس

واریانس نمونه را می‌توانیم از فرمول زیر بدست آوریم.

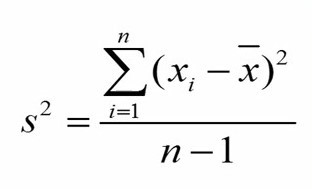
به عبارت دیگر، واریانس از مجموع توان دوم انحراف‌ها از میانگین تقسیم بر درجه آزادی حاصل می‌شود. نکته‌ای باید توجه کنیم این است که عموماً برای اندازه‌گیری پراکندگی از انحراف استاندارد که ریشه دوم واریانس است استفاده می‌کنیم. چون مقیاس آن مشابه با مقیاس‌ داده‌ها است.

بررسی پراکندگی داده ها: انحراف استاندارد یا دامنه میان چارکی؟

انتخاب بین انحراف استاندارد و دامنه میان چارکی دقیقاً به این موضوع ارتباط دارد که برای کمیت تمایل به مرکز از میانگین استفاده کنیم یا از میانه؟ یعنی میانگین همیشه با انحراف استاندارد و میانه با دامنه میان چارکی گزارش می‌شود.

به عبارت بهتر، چنانچه داده‌های ما انحراف مشخصی از توزیع نرمال نداشته باشد و توزیع داده‌های ما متقارن باشد، از میانگین و انحراف معیار استفاده می‌کنیم.

اما اگر داده‌‌های ما دارای چولگی یا کشیدگی باشد یا در داده‌های ما مشاهده‌های پرت یا دورافتاده وجود دارد، از میانه و دامنه میان چارکی استفاده می‌کنیم.

نکته‌ای باید توجه کنیم این است محدوده یک انحراف معیار از میانگین حدود 68 % از داده‌ها قرار دارد. در حالی در محدوده دامنه میان چارکی 50 % از اعداد قرار می‌گیرد.