مدل‌های خطی با اثرات آمیخته (قسمت اول-مفهوم)

در این مقاله با مدل‌های خطی با اثرات آمیخته (Linear Mixed-effects models) آشنا می‌شویم. برای فهم بهتر این مقاله باید مقالات مربوط به آنالیز واریانس و رگرسیون خطی را مطالعه نمایید.

آشنایی با مدل‌های خطی با اثرات آمیخته

اصطلاح آمیخته برای این‌گونه مدل‌ها به این دلیل استفاده می‌شود که ما در این مدل‌ها اثرات ثابت (Fixed) و تصادفی (Random) را همزمان داریم.

تعریف اثرات ثابت (Fixed effects):

کمیت‌هایی که در یک جمعیت ثابت و بدون تغییر هستند را اثرات ثابت می‌نامیم. مثلاً میانگین یک جمعیت یا پارامترهای موجود در یک جمعیت که ما آن‌ها را برآورد می‌کنیم همگی ثابت هستند.

تعریف اثرات تصادفی (Random effects):

اثرات تصادفی پارامترهایی هستند که بین گروه‌های مختلف متغیر وابسته متغیر هستند. به عنوان مثال اگر ما روی یک فرد در چند زمان اندازه‌‌گیری های تکراری داشته باشیم، میانگین این اندازه‌ها می‌تواند یک پارامتر باشد. در این صورت هر فرد در جامعه می‌تواند یک تخمین منحصر به فرد برای خودش داشته باشد و متغیر فرد (subject) را می‌توانیم به عنوان یک متغیر تصادفی در مدل تعریف کنیم.

مثال برای مدل‌های خطی با اثرات آمیخته

فرض کنید چهار فرد در یک مدت زمان خاص یک نوع رژیم غذایی را مصرف می‌کنند. وزن این افراد را قبل از مصرف رژیم غذایی، یک هفته پس از آن و دو هفته پس از دریافت رژیم غذایی اندازه‌گیری می‌کنیم (شکل 1).

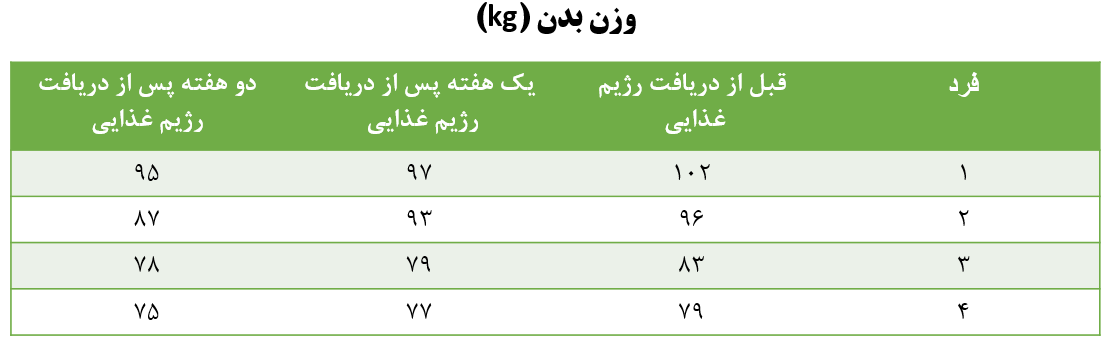
شکل 1. اندازه‌گیری وزن بدن

اگر وزن‌های افراد را در یک نمودار پراکنش دو طرفه پلات کنیم شکل زیر را خواهیم داشت:

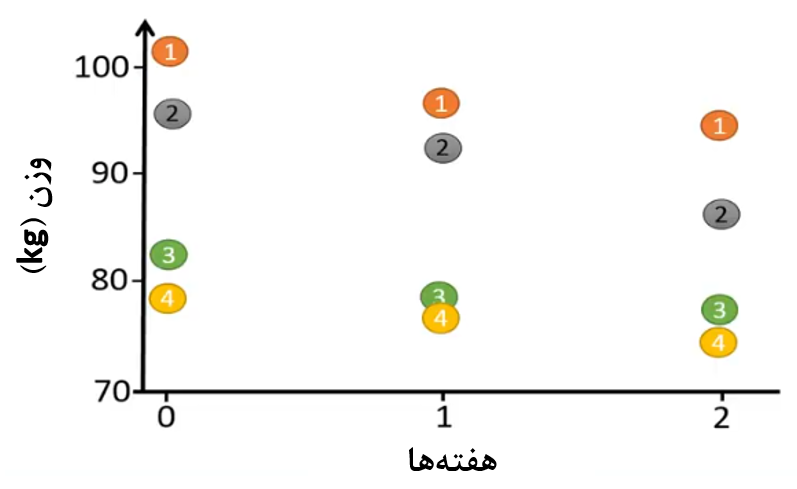
شکل 2. نمایش وزن افراد در قالب نمودار دو طرفه

در شکل 2 اطلاعات مربوط به هر فرد را با شماره نشان داده‌ایم.

فرض کنید می‌خواهیم میزان کاهش وزن افراد به ازای هر هفته را تخمین بزنیم. در این صورت از روش رگرسیون خطی استفاده می‌کنیم و یک خط بین نقاط برازش می‌کنیم (شکل 3).

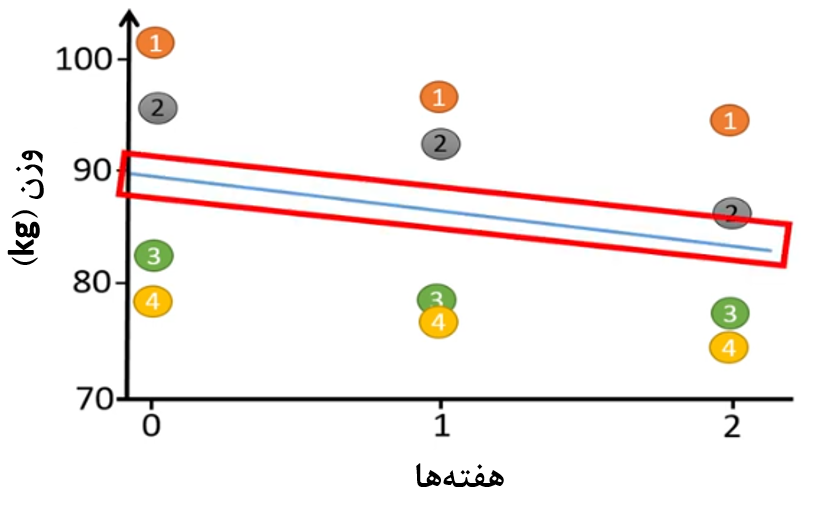
شکل 3. برازش خط رگرسیونی از بین نقاط برای تخمین میزان کاهش وزن

معادله خط رگرسیونی در شکل 3 به شرح زیر است:

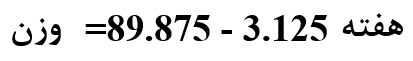
عرض از مبدأ این خط 875/89 و شیب خط 125/3- است. عرض از مبدأ (89.857) میانگین وزن افراد جمعیت قبل از شروع دریافت رژیم غذایی را نشان می‌دهد. شیب خط (3.125-)، متوسط کاهش وزن در هر هفته را نشان می‌دهد. به این معنی که افراد ما بطور متوسط در طول هر هفته 3.125 کیلوگرم وزن کم کرده‌اند.

الان می‌خواهیم بدانیم که آیا متوسط کاهش وزن در هر هفته (شیب خط) آیا معنی‌دار است؟ به این منظور آزمون فرضیات را مطرح می‌کنیم.

آزمون فرضیات

آزمون فرضیات را برای شیب خط رگرسیون بصورت زیر تعریف می‌کنیم:

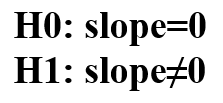
آیا می‌توانیم فرض صفر مبنی برابری شیب خط رگرسیون با صفر را رد کنیم؟ اگر بتوانیم این فرض را رد کنیم به این معنی است که رژیم غذایی ما واقعاً بر وزن افراد موثر است.

محاسبه P-value و نتیجه‌گیری

در این آزمایش مقدار P-value را عدد 0.372 بدست آورده‌ایم. چون مقدار P-value از عدد 0.05 بزرگتر است، نمی‌توانیم فرض صفر را رد کنیم. بنابراین نتیجه می‌گیریم که رژیم غذایی ما موثر نبوده است.

اما همانطور که ملاحظه می‌کنیم ما بطور متوسط در هر هفته 3.125 کیلوگرم کاهش وزن داشته‌ایم و عجیب است که این مقدار کاهش وزن معنی‌دار نیست. اگر به هر 4 نمونه هم دقت کنیم، می‌بینیم که هر 4 فرد ما در طول زمان کاهش وزن‌ را تجربه کرده‌اند.

اما چرا با اینکه تمام افراد ما در طول زمان کاهش وزن داشته‌اند، این مقدار کاهش وزن معنی‌دار نیست؟ پاسخ این سوال را در ادامه خواهیم داد.

اگر ما به جای رگرسیون معمولی از مدل خطی با اثرات آمیخته (Linear mixed effects model) استفاده کنیم، مقدار P-value‌ ما 0.001 بدست می‌آید و به راحتی می‌توانیم فرض صفر را رد کنیم و نتیجه بگیریم که شیب خط ما با عدد صفر تفاوت معنی‌دار دارد.

اما چرا چنین تفاوت بزرگی بین نتیجه حاصل از رگرسیون خطی و مدل خطی با اثرات آمیخته وجود دارد؟

مقایسه رگرسیون خطی ساده و مدل خطی با اثرات آمیخته

به شکل 4 دقت کنید. زمانی که ما از رگرسیون خطی ساده استفاده می‌کنیم، نقاط داده‌ها از خط رگرسیونی بسیار دور هستند. چون 4 فرد انتخاب شده از جمعیت در ابتدای آزمایش، وزن‌های مختلفی داشته‌اند، لذا نقاط از خط رگرسیون فاصله دارند.

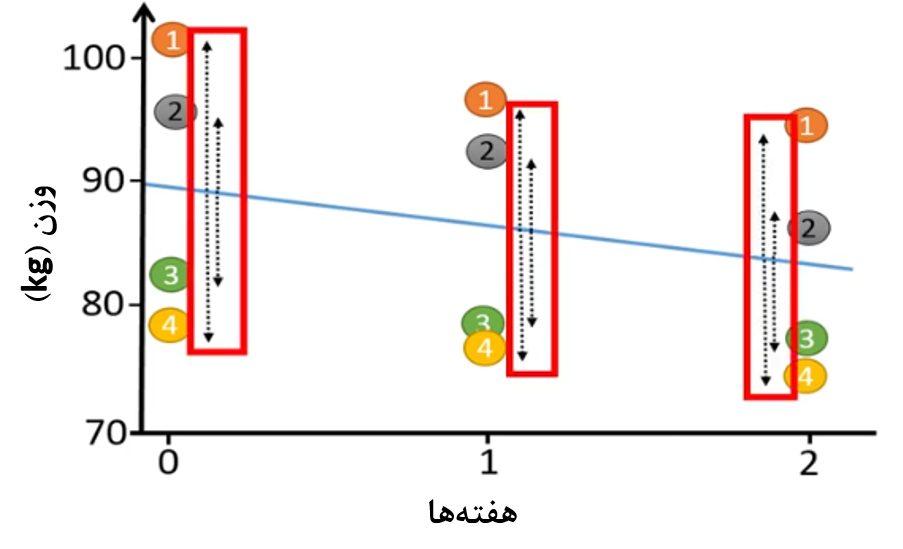
شکل 4. فواصل نقاط نسبت به خط رگرسیون معمولی

در حقیقت ما نباید به وزن افراد در ابتدا و قبل از شروع آزمایش توجه کنیم. ما باید به میزان کاهش وزن هر فرد در طول زمان نسبت به وزن اولیه خودش دقت کنیم. برای اینکه بتوانیم تنوع وزن افراد در ابتدای آزمایش را حذف کنیم، از مدل خطی با اثرات آمیخته استفاده می‌کنیم.

در این مدل ما افراد را به عنوان اثر تصادفی در مدل تعریف می‌کنیم تا بتوانیم برای هر فرد شیب و عرض از مبدأ جداگانه تخمین بزنیم (شکل 5).

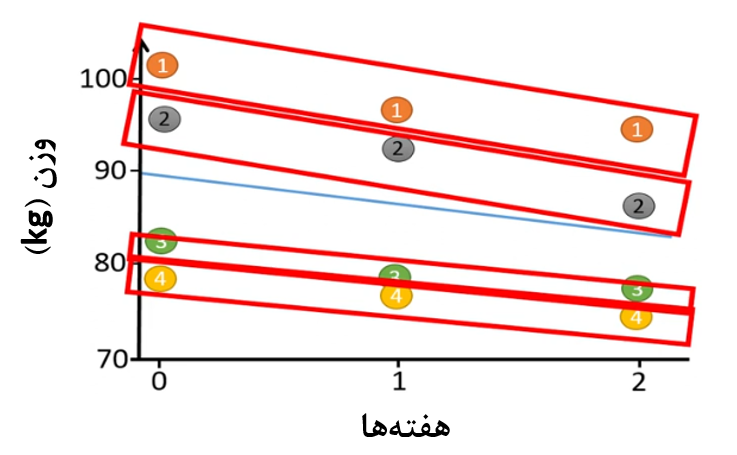
شکل 5. در نطر گرفتن داده‌های هر فرد بصورت جداگانه در مدل

با استفاده از مدل خطی با اثرات آمیخته می‌توانیم در مدل برای هر فرد یک خط جداگانه برازش کنیم.

اگر از یک مدل با عرض از مبدأ تصادفی و شیب خط ثابت استفاده کنیم شکل 6 را خواهیم داشت:

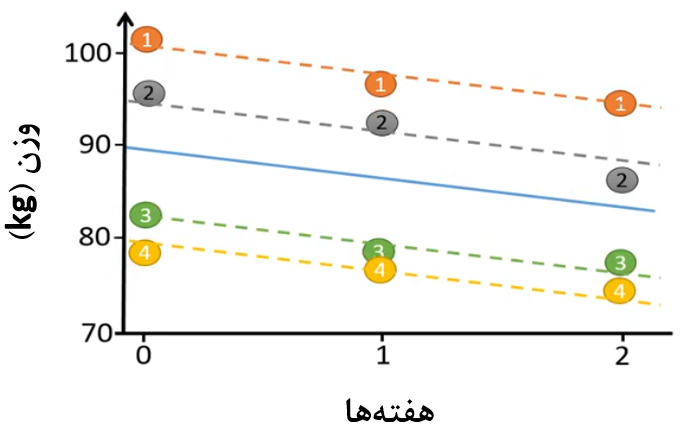
شکل 6. مدل با عرض از مبدأ تصادفی و شیب خط ثابت

بنابراین می‌توانیم تصور کنیم که این مدل شامل افرادی است که در ابتدای آزمایش وزن متفاوت دارند. ولی با مصرف رژیم غذایی شیب کاهش وزن تمام این افراد مشابه است.

اما تشابه شیب کاهش وزن افراد در طول زمان واقعی به نظر نمی‌رسد. چرا که افراد مختلف ممکن است نرخ متفاوتی از کاهش وزن را در طول یک دوره داشته باشند. اما برای سادگی مسئله می‌توانیم فرض کنیم که هر چهار فرد دارای شیب کاهش مساوی هستند. توجه داشته باشید که ما می‌توانیم شیب را هم به عنوان یک متغیر تصادفی در مدل لحاظ کنیم که در مقاله بعد به این موضوع می‌پردازیم.

مدل دارای عرض از مبدأ تصادفی و شیب ثابت

در مدل با عرض از مبدأ تصادفی، هر فرد دارای یک عرض از مبدأ مخصوص به خودش می‌باشد. اگر مدل مربوطه را در یک نرم افزار آماری تعریف کنیم، می‌توانیم مقادیر عرض از مبدأ هر فرد را بدست بیاوریم. این مقادیر فاصله عرض از مبدأ هر فرد را نسبت به عرض از مبدأ کل نشان می‌دهد.

اگر خاطرتان باشد معادله خط رگرسیون اصلی ما به شرح زیر بود:

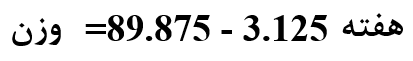
عرض از مبدأ برای خط اصلی ما 89.875 است. اگر عرض از مبدأ را در مدل بصورت تصادفی تعریف کنیم برای هر فرد یک عرض از مبدأ منحصر به فرد خواهیم داشت. در این صورت عرض از مبدأ برای افراد مختلف به شرح می‌باشد:

این مقادیر فاصله عرض از مبدأ هر فرد را نسبت به عرض از مبدأ خط اصلی نشان می‌دهد. به عنوان مثال، عرض از مبدأ فرد اول 11.2 واحد بیشتر از عرض از مبدأ خط اصلی است. اگر 11.2 واحد به عرض از مبدأ خط اصلی اضافه کنیم، عرض از مبدأ خط مربوط به فرد اول بدست می‌آید. برای بقیه افراد هم می‌توانیم به همین طریق عرض از مبدأ افراد را بدست بیاوریم.

کاهش خطا در مدل آمیخته

پس الان چهار خط داریم که نقاط به این خطوط بسیار نزدیکتر هستند. نزدیکی نقاط به این خطوط باعث کاهش خطای استاندارد و کاهش P-value نهایی می‌شود (شکل 7).

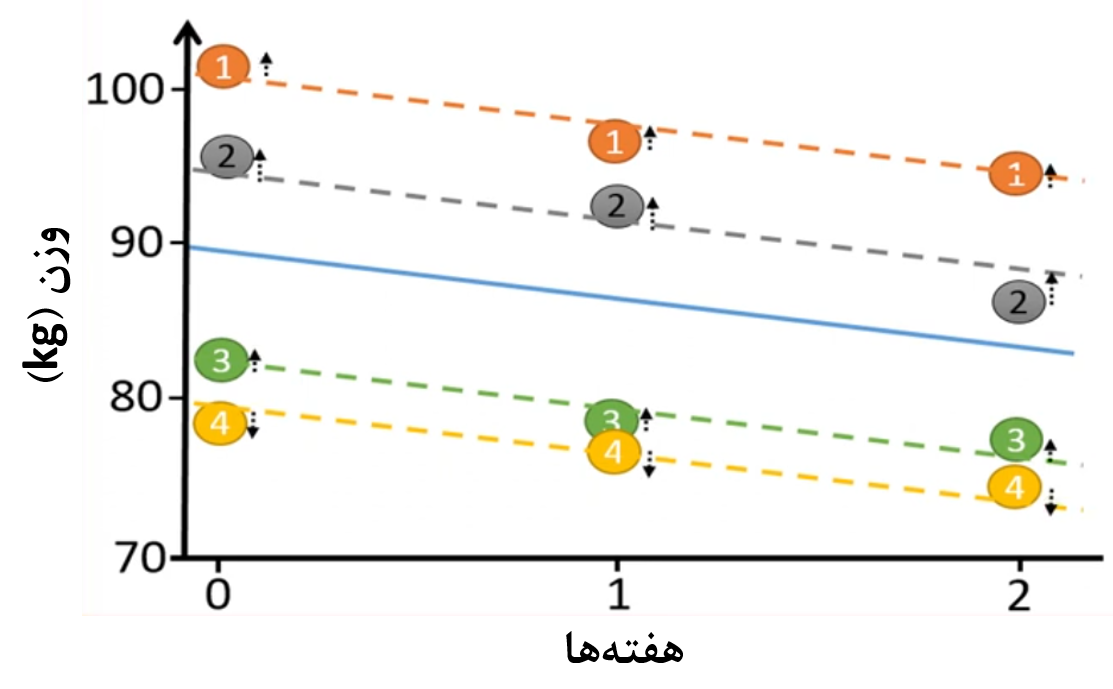
شکل 7. برازش خطوط برای هر فرد و نمایش فاصله نقاط نسبت به خطوط

در شکل زیر مجموع مربعات خطا در هر دو حالت رگرسیون خطی ساده و مدل خطی با اثرات آمیخته مشاهده می‌کنید.

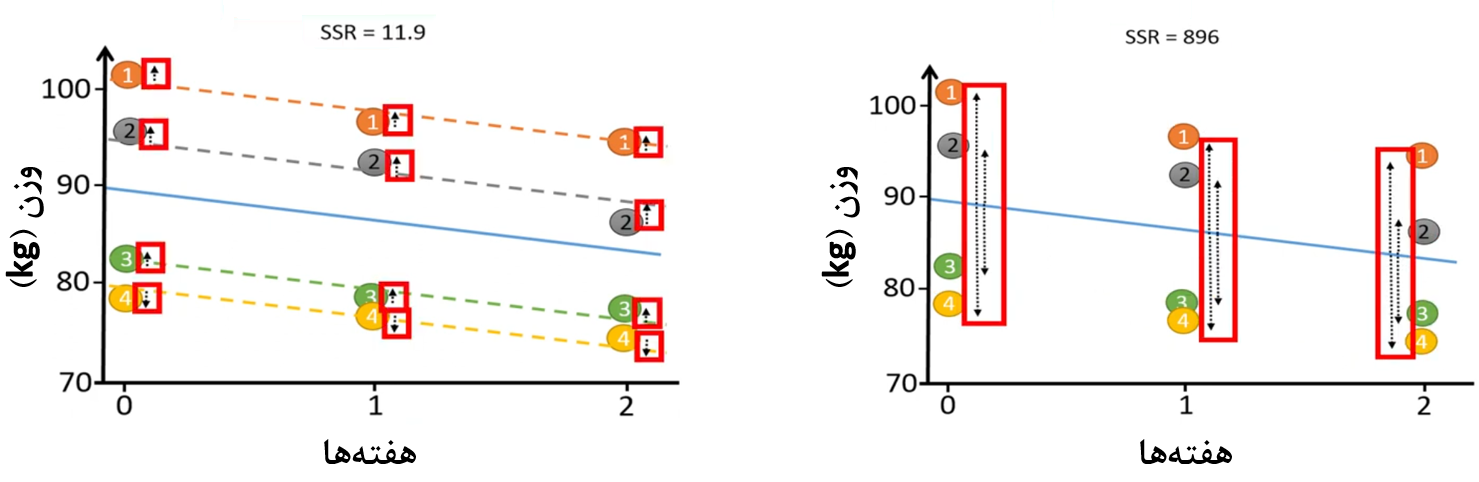
شکل 8. مقایسه رگرسیون خطی ساده و مدل خطی با اثرات آمیخته

مطابق شکل 8، مجموع مربعات خطا را در حالت مدل خطی با اثرات آمیخته 11.9 و در حالت رگرسیون خطی ساده 896 بدست آورده‌ایم. چرا که در رگرسیون خطی ساده فاصله نقاط نسبت به خط خیلی زیاد است. اما در مدل خطی با اثرات آمیخته فاصله نقاط نسبت به خطوط بسیار کاهش می‌یابد.

چرا به این مدل خطی، آمیخته گفته می‌شود؟

به دلیل اینکه در این مدل اثرات ثابت و تصادفی همزمان مورد استفاده قرار می‌گیرد، این مدل را مدل خطی با اثرات آمیخته می‌نامیم.

تفاوت عرض از مبدأ خطوط مربوط به هر یک از افراد، نسبت به عرض از مبدأ خط اصلی یک متغیر تصادفی برای ما می‌سازد. این مقادیر دارای توزیع نرمال با میانگین صفر و واریانس تخمینی توسط مدل می‌باشد.

چون در این مدل فقط عرض از مبدأ بین افراد متفاوت است، این مدل، عرض از مبدأ تصادفی (random intercept) نامیده می‌شود. در حقیقت اگر ما از جامعه بطور تصادفی نمونه‌های تصادفی انتخاب کنیم، انتظار داریم که توزیع وزن افراد از توزیع نرمال تبعیت کند.

مقایسه رگرسیون خطی چندگانه و مدل خطی با اثرات آمیخته

فرض کنید به جای اینکه متغیر فرد (subjects) را در مدل به عنوان یک فاکتور تصادفی (random factor) لحاظ کنیم، در قالب رگرسیون خطی چندگانه ما متغیر فرد (subjects) را به عنوان یک فاکتور ثابت در مدل در نظر بگیریم. اگر متغیر فرد را در مدل بصورت ثابت در نظر بگیریم، به این مفهوم است که ما می‌خواهیم افراد مختلف را با هم مقایسه کنیم. در این صورت افراد ما دیگر بطور تصادفی از یک جمعیت انتخاب نمی‌شوند.

نتایج هر دو مدل رگرسیون خطی چند گانه و مدل خطی با اثرات آمیخته را در شکل 8 نشان داده‌ایم.

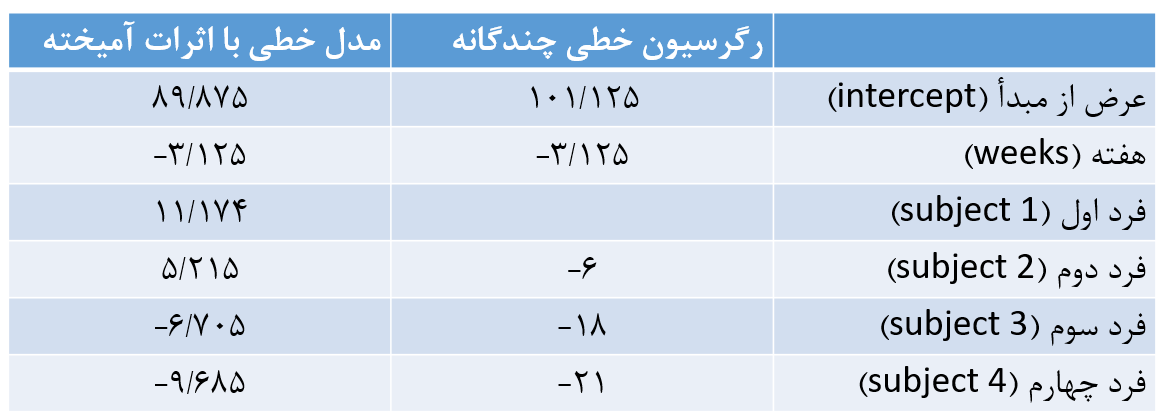
شکل 9. مقایسه نتایج رگرسیون خطی چندگانه و مدل خطی با اثرات آمیخته

توضیح نتایج

توجه کنید که شیب خطوط در هر دو مدل با هم برابر (3.125-) است. اما عرض از مبدأ دو مدل با هم متفاوت است. در رگرسیون خطی چندگانه عرض از مبدأ 101.125 و در مدل خطی با اثرات آمیخته عرض از مبدأ 89.875 بدست آمد.

در رگرسیون خطی چندگانه یک فرد به عنوان طبقه رفرنس قرار می‌گیرد و بقیه افراد با آن فرد مقایسه می‌شوند. عرض از مبدأ در رگرسیون خطی چندگانه (101.125) مربوط به فرد اول است. این در حالی است که در مدل خطی با اثرات آمیخته عرض از مبدأ مربوط به خط اصلی است که از میانگین چهار فرد حاصل می‌شود. در رگرسیون خطی چندگانه، اعداد 6-، 18- و 21- فاصله عرض از مبدأ افراد 2، 3 و 4 را نسبت به فرد 1 (رفرنس) نشان می‌دهد. در حالی‌که در مدل آمیخته اعداد 11.17، 5.21، 6.70- و 9.68- فاصله هر فرد نسبت به خط اصلی را نشان می‌دهد.

مشکل دیگری که در رگرسیون خطی چندگانه وجود دارد، مفروض استقلال مشاهدات است که نقض می‌شود. چراکه مشاهدات ما مستقل نیستند و مثلاً سه مشاهده اول مربوط به فرد اول، سه مشاهده دوم مربوط به فرد دوم و ….. است.

مزیت استفاده از مدل‌های خطی با اثرات آمیخته نسبت آنالیز واریانس با اندازه‌های مکرر

در استفاده از مدل خطی با اثرات آمیخته نسبت به آنالیز واریانس با اندازه‌های تکراری چندین مزیت وجود دارد.

اولین مزیت این است که در مدل خطی با اثرات آمیخته ما می‌توانیم ضرایبی مانند شیب خطوط را تخمین بزنیم. مزیت دیگر استفاده از مدل خطی با اثرات آمیخته این است که در این مدل اگر داده‌های گم شده داشته باشیم، باز هم به خوبی می‌توانیم ضرایب را تخمین بزنیم. در حالی‌که‌ در آنالیز واریانس با اندازه‌های تکراری اگر یک فرد در طول زمان یک مشاهده گم شده داشت، تمام اطلاعات مربوط به آن فرد از آزمایش حذف می‌شود. این امر منجر به کاهش حجم نمونه و قدرت آزمون می‌شود.

در آنالیز واریانس با اندازه‌های تکراری متغیر وابسته از نوع پیوسته در نظر گرفته می‌شود. در حالی‌که در مدل‌های خطی با اثرات آمیخته تعمیم یافته (generalized linear mixed-effects model) متغیر وابسته می‌تواند از نوع باینری یا شمارشی نیز باشد. همچنین متغیر تکراری همیشه به عنوان یک متغیر طبقه‌ای در نظر گرفته می‌شود. این موضوع به این مفهوم است که نقاط زمانی باید برای تمام افراد کاملاً مشابه باشد. اما در مدل خطی با اثرات آمیخته متغیر مستقل می‌تواند از نوع پیوسته باشد که به این مفهوم است که نقاط زمانی می‌تواند برای افراد مختلف متفاوت باشد.

توجه کنید که مفروضات مدل خطی با اثرات آمیخته با بقیه مدل‌های خطی مشابه است. به عنوان مثال، در این مدل متغیر یا متغیرهای مستقل باید با متغیر پاسخ بطور خطی ارتباط داشته باشد و باقیمانده ها نیز دارای توزیع نرمال باشند. همچنین مدل خطی با اثرات آمیخته فرض می‌کند که مشاهدات مربوط به هر فرد (کلاستر) دارای همبستگی مثبت هستند.

در مقاله دوم از این بخش بررسی می‌کنیم که چگونه می‌توانیم شیب خطوط را هم بصورت تصادفی در مدل تعریف کنیم.