تحلیل مسیر در آموس AMOS

در این مقاله نحوه انجام تحلیل مسیر با استفاده از متغیرهای آشکار را در نرم افزار AMOS با هم بررسی می‌کنیم.  مدلی که در این مقاله تجزیه و تحلیل می‌کنیم از داده‌های مربوط به مقاله زیر گرفته شده است.

Zhou, J., Yang, Y., Qiu, X., Yang, X., Pan, H., Ban, B., et al. (2016). Relationship between anxiety and burnout among Chinese physicians: A moderated mediation model. PLoS ONE 11(8): e0157013. doi:10.1371/journal.pone.0157013

مدلی که برای تحلیل مسیر در نظر می‌گیریم به شرح زیر است:

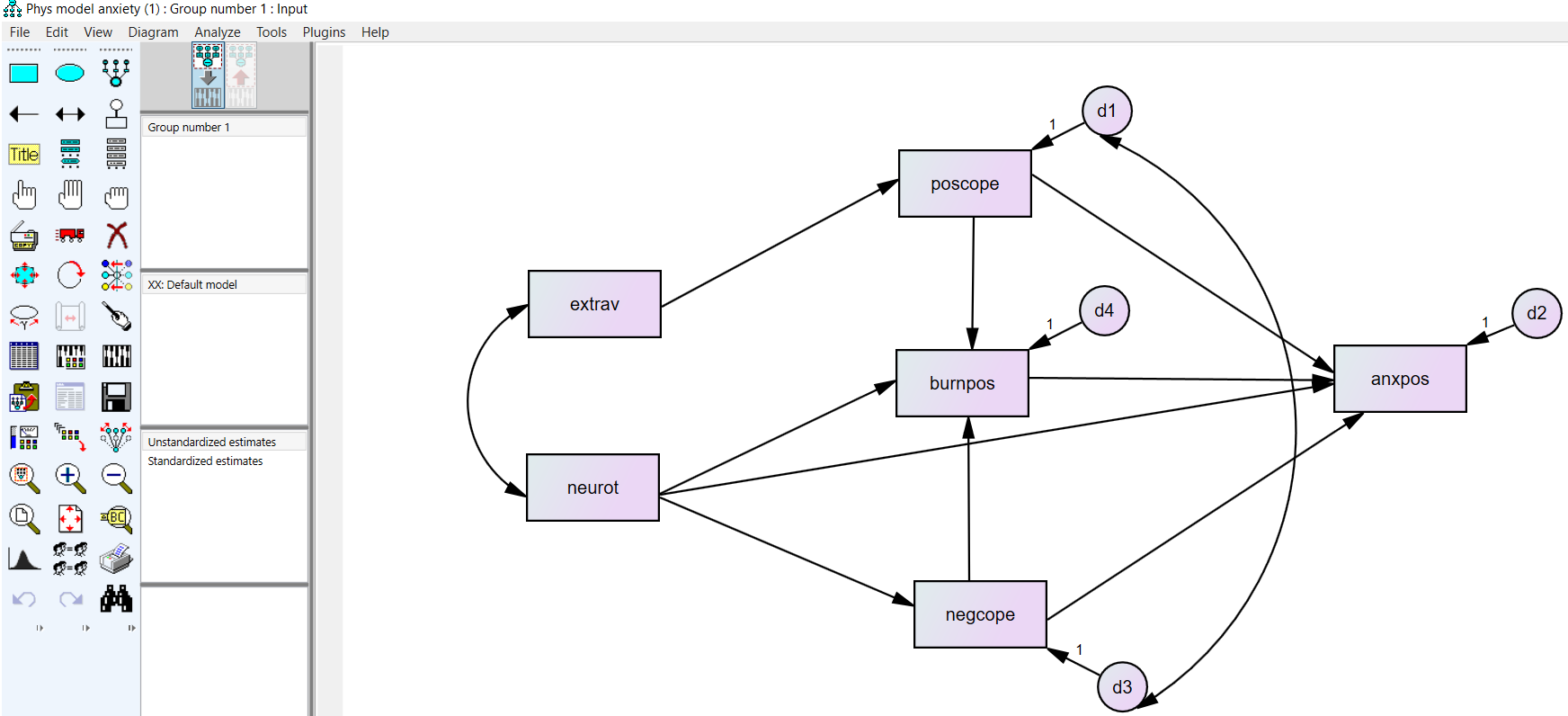
متغیرهای مورد استفاده در مدل به شرح زیر هستند:

Extrav: برونگرایی (محاسبه شده از 11 گویه، α=0.793)

neurot: روان رنجور خویی (محاسبه شده از 12 گویه، α=0.844)

poscope: مقابله مثبت (محاسبه شده از 10 گویه، α=0.815).

negcope: مقابله منفی (محاسبه شده از 10 گویه، α=0.803).

burnpos: فرسودگی شغلی (محاسبه شده از 10 گویه، α=0.810).

anxpos: اضطراب (محاسبه شده از 15 گویه، α=0.932).

متغیرهای درون‌زا و برون‌زا در مدل تحلیل مسیر

در تحلیل مسیر متغیرهای برون‌زا آن‌هایی هستند که هیچ فلش یک جهته‌ای از متغیرهای دیگر به آن‌ها اشاره نمی‌کند. در مدل ما دو متغیر extrav و neurot برون‌زا به حساب می‌آیند. متغیرهای درون‌زا آن‌هایی هستند که دارای فلش‌های یک جهته از سایر متغیرها هستند. در مدل ما متغیرهای poscope، negcope، burnpos و anxpos متغیرهای درون‌زا هستند. متغیرهای وابسته یا درون‌زا در مدل علاوه بر اینکi فلش یک جهته دریافت می‌کنند، دارای یک عبارت خطا (باقیمانده) نیز هستند. برای نمایش عبارت خطا از دایره استفاده می‌‌شود.

نحوه اجرای مدل

برای اجرای یک مدل گام‌های زیر را اجرا کنید :

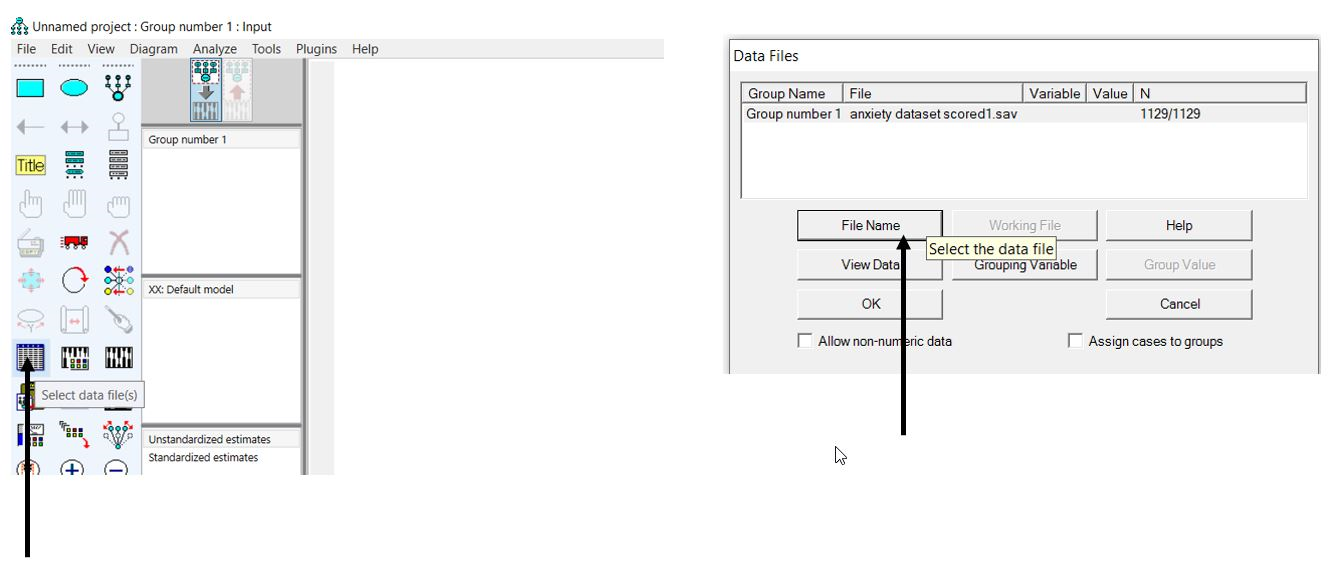
مانند شکل بالا داده‌‌های خود را وارد نرم افزار AMOS کنید. به این صورت که روی آیکون «select data file(s)» کلیک کنید. وقتی باکس مربوطه باز شد، روی «File name»کلیک کنید و از مسیر مربوطه فایل داده‌های خود را انتخاب کنید.

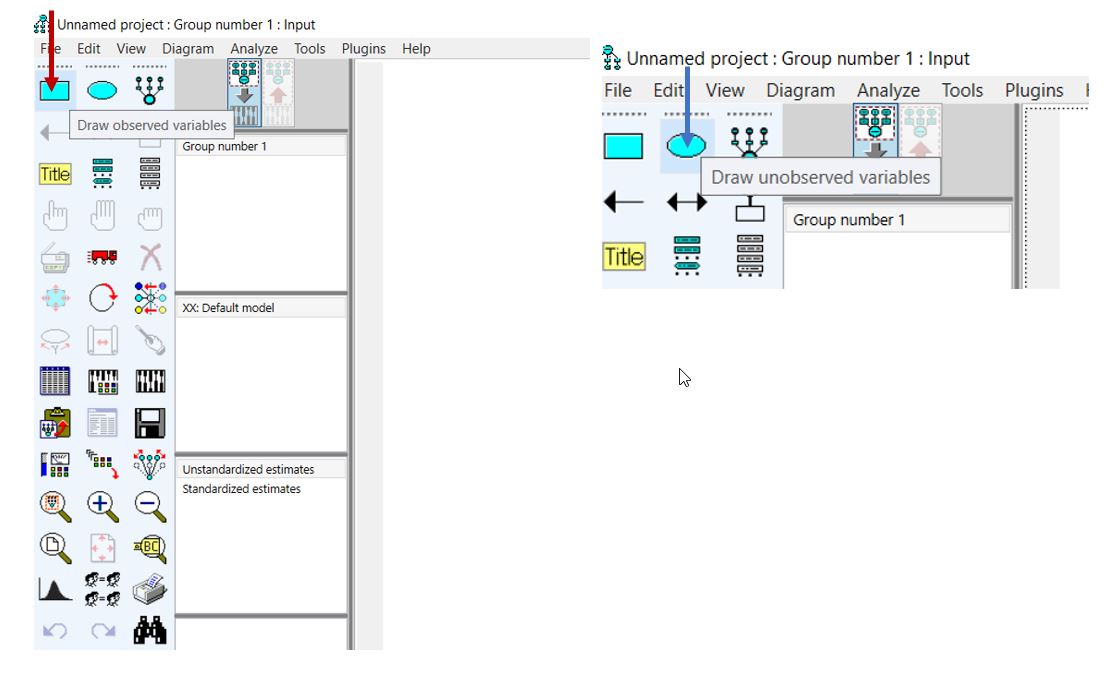
پنل سمت چپ در نرم افزار آموس امکان رسم اشکال و ویرایش آن‌ها را به ما می‌دهد. به عنوان مثال، برای نمایش متغیرهای آشکار «Observed variables» از مستطیل و برای ترسیم متغیرهای پنهان «Unobserved variables» از دایره استفاده می کنیم. این موضوع را در شکل بالا نشان داده‌ایم.

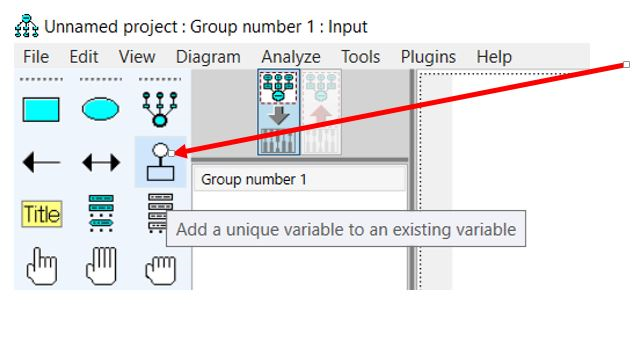
برای نشان دادن نماد مربوط به خطا از آیکون «Add a unique variable to an existing variable» استفاده می کنیم (شکل بالا).

از آیکون  «Analysis properties» تنظیمات مربوط به آنالیز را انجام می‌دهیم.

مطابق شکل بالا، اگر روی آیکون «Analysis properties»کلیک کنیم، در برگه اول با نام «Estimation» می‌توانیم روش تخمین را مشخص کنیم. روش تخمین پیش فرض، حداکثر درستنمایی «Maximum likelihood» نام دارد.

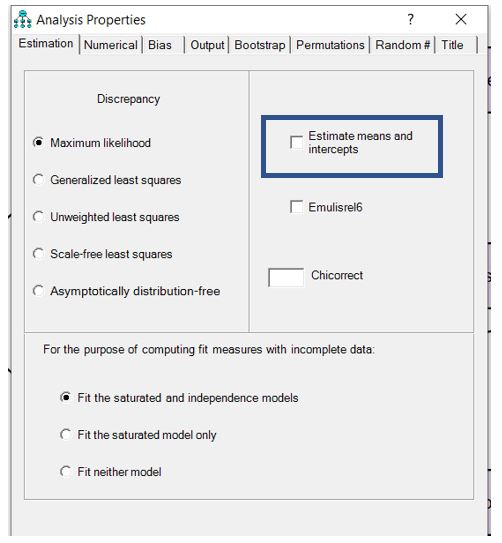
در قسمت سمت راست برگه «Estimation» بخشی به نام «Estimation means and intercepts» وجود دارد (شکل بالا). این بخش زمانی استفاده می‌شود که در بین اطلاعات، داده گم شده وجود دارد. در مثال ما داده گم شده وجود ندارد. بنابراین از فعال کردن این بخش اجتناب می کنیم.

در برگه «Output» دو بخش «Standardized estimates» و «Squared multiple correlations» را فعال می کنیم. فعال کردن این دو بخش باعث می‌شود که نرم افزار ضرایب مسیر استاندارد شده و همچنین ضرایب تبیین را برای هر یک از متغیرهای وابسته (درون‌زا) محاسبه کند (شکل بالا).

در نهایت روی آیکون «Calculate estimates» کلیک می‌کنیم تا آنالیز انجام شود (شکل بالا).

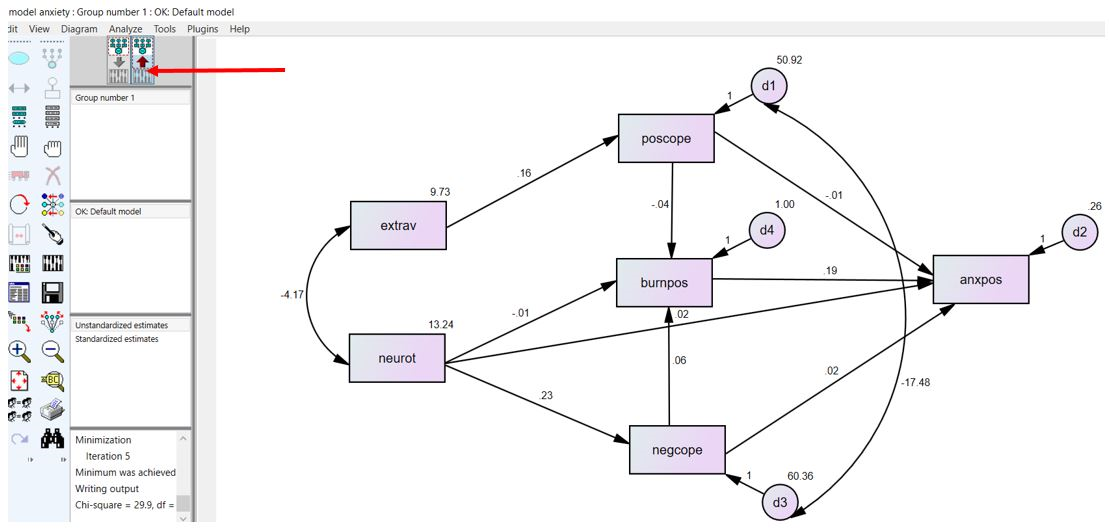
در قسمت بالای صفحه نمایش یک دکمه قرمز وجود دارد. زمانی که روی این دکمه کلیک کنیم، پارامترهای تخمین زده شده روی نمودار نشان داده می‌شود (شکل بالا).

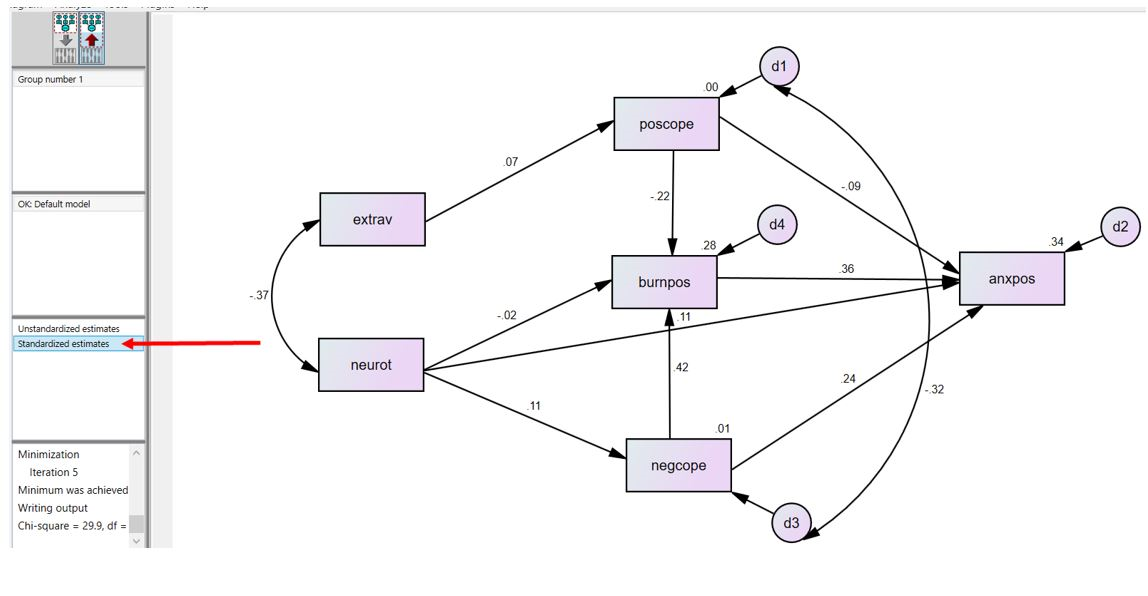
برای نمایش ضرایب مسیر استاندارد شده روی نمودار، از گزینه «Standardized estimates» استفاده می‌کنیم (شکل بالا).

در نهایت روی آیکون «View Text» کلیک می‌کنیم تا خروجی نرم افزار نمایش داده شود:

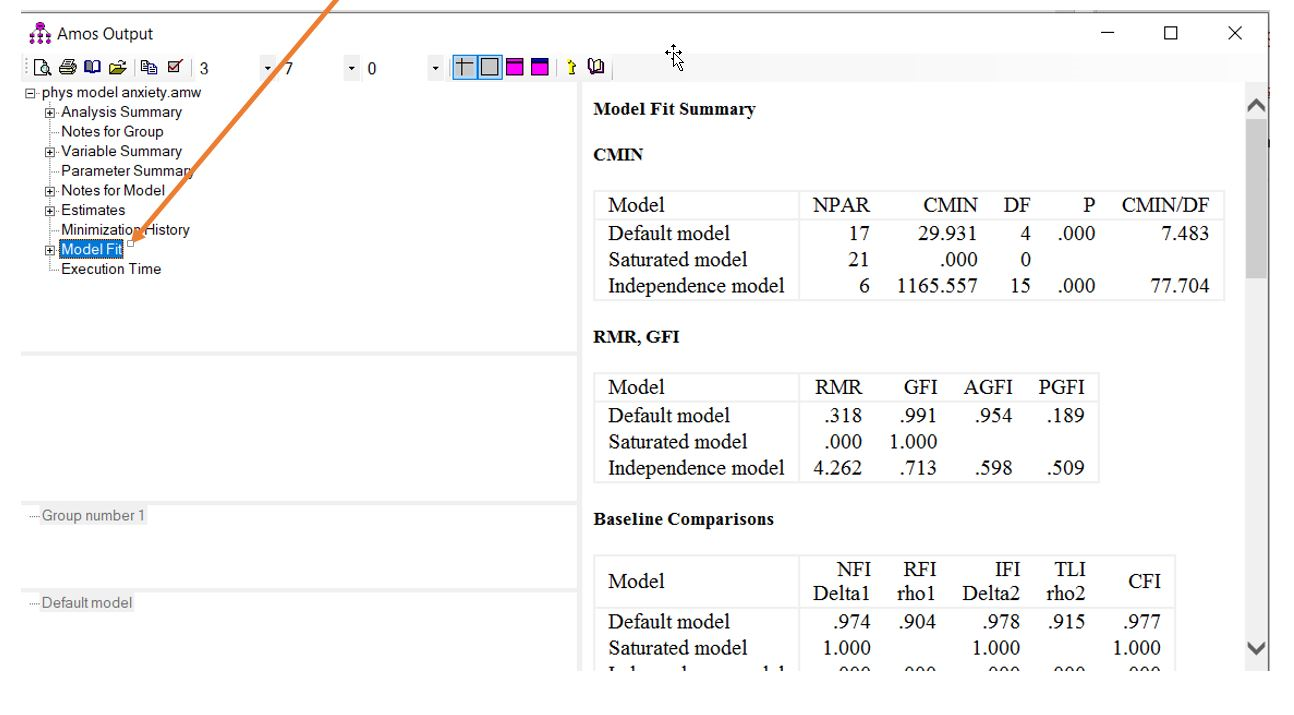
برای مشاهده شاخص‌های برازش مدل در خروجی نرم افزار مانند شکل بالا روی “Model Fit” کلیک می‌کنیم.

بررسی شاخص‌های برازش مدل در تحلیل مسیر (Model Fit)

به شاخص‌های برازش مدل در شکل زیر دقت کنید.

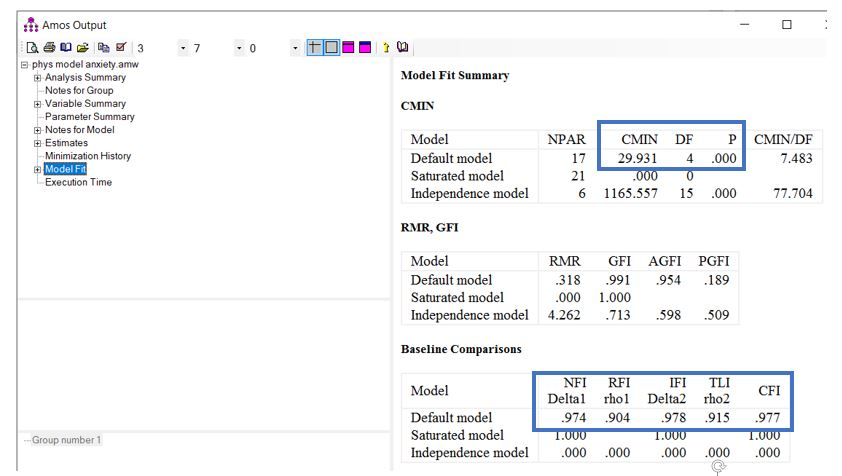
عبارت “CMIN” که در خروجی ظاهر می‌شود، مقدار کای اسکوئر است که نیکویی برازش مدل را نشان می‌دهد. آزمون کای اسکوئر برای ارزیابی مدل استفاده می‌شود و به ما می‌گوید آیا مدل ما از یک مدلی که کاملا بر داده‌ها مطابقت دارد، تبعیت می‌کند یا خیر؟

عبارت “DF” درجه آزادی و “P” مقدار سطح معنی‌داری را نشان می‌دهد. چنانچه مقدار P کوچکتر از 0.05 باشد، فرض صفر ما رد می‌شود و نتیجه می‌گیریم که مدل ما از مدلی که کاملا بر داده‌ها مطابقت دارد، تبعیت نمی‌کند.

شاخص تناسب هنجاری (NFI)، شاخص تناسب نسبی (RFI)، شاخص تناسب افزایشی (IFI)، شاخص تناسب مقایسه ای (CFI) و شاخص تاکر-لوئیس (TLI به عنوان شاخص تناسب غیر هنجاردار یا NNFI نیز شناخته می شود)، همه شاخص‌های برازش افزایشی یا مقایسه‌ای هستند (یعنی به موجب آن برازش یک مدل را در برابر مدل صفر یا مستقل مقایسه می‌کنند).

این شاخص ها معمولاً بین 0 و 1 متغیر هستند (اگرچه ممکن است مقادیر کمی بیشتر از 1 در برخی از آنها باشد). مقادیر بالاتر از 90. برای این شاخص‌ها برازش قابل قبولی از مدل را نشان می‌دهند. اگرچه مقادیر بالاتر از 0.95 برای این شاخص‌ها، برازش کاملا مطلوب مدل را نشان می‌دهند.

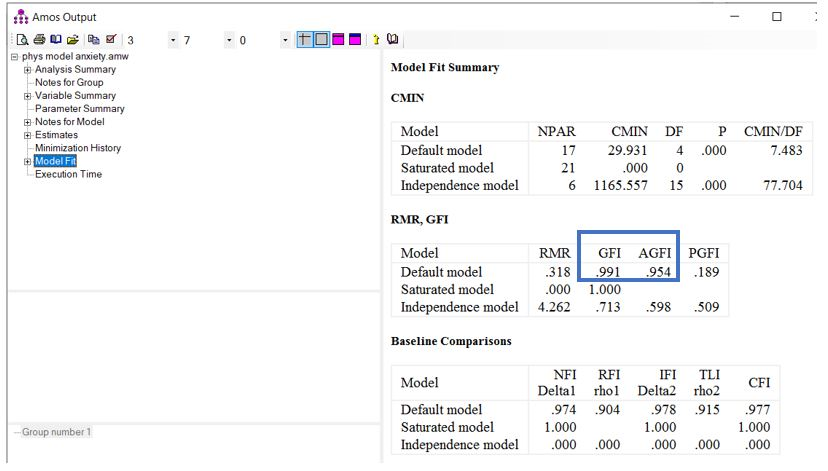
به شکل بالا دقت کنید. شاخص نیکویی برازش (GFI) و شاخص نیکویی برازش تعدیل شده (AGFI) شاخص‌های برازش مطلق هستند (Kline, 2016). شاخص AGFI نشان دهنده تعدیل GFI برای تعداد پارامترهای برآورد شده است. محدوده GFI و AGFI از 0 تا 1 است که مقادیر بالاتر نشان دهنده تناسب بیشتر است (Byrne, 2010). مقادیر > 0.90 یا 0.95 معمولاً نشان دهنده برازش مدل قابل قبول تا خوب در نظر گرفته می‌شوند .

توجه به این نکته مهم است که در مواردی که داده‌های گمشده وجود داشته باشد، این شاخص‌ها در خروجی AMOS ظاهر نمی‌شوند.

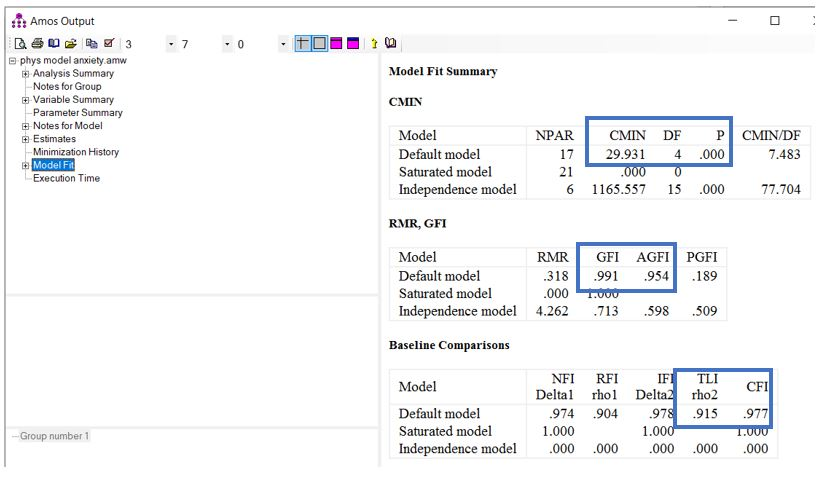
مطابق شکل بالا، نتایج آزمون کای اسکوئر نشان می‌دهد که مدل ما بطور معنی‌داری از مدلی که با کاملا بر داده‌ها مطابقت دارد، فاصله دارد. شاخص‌های GFI و AGFI هر دو برازش مطلوب مدل را نشان می‌دهد (هر دو بزرگتر از 0.9). دو شاخص TLI و CFI نیز هر دو بزرگتر از 0.9 هستند و هر دو نشان دهنده برازش مطلوب مدل هستند.

به شکل بالا دقت کنید. ریشه دوم خطای تقریب (RSME) نیز می‌تواند به عنوان یک شاخص برازش مطلق در نظر گرفته شود. برای RMSE، مقدار 0 نشان دهنده بهترین برازش و مقادیر بالاتر از 0 نشان دهنده فاصله نسبت به برازش مطلوب است. در مدل‌ها مقادیر 0.05 و کمتر از آن به عنوان برازش مطلوب مدل در نظر گرفته می‌شود. مقادیر 0.05 تا 0.1 به عنوان مقادیر قابل قبول برای برازش در نظر گرفته می‌شود. مقادیر بزرگتر از 0.1 نشان دهنده مشکل جدی در برازش مدل است.

برای مدل ما RMSE مقدار 0.076 بدست آمده است که بین 0.05 (برازش مطلوب) تا 0.1 (برازش ضعیف) قرار قرار دارد.

روش دیگر برای ارزیابی برازش مدل، آزمون PCLOSE‌ است. این آزمون بر مبنای RMSE انجام می‌شود. اگر فرض کنیم که RMSE کوچکتر از 0.05 باشد، چنانچه مقدار PCLOSE بزرگتر از 0.05 باشد، می‌توانیم این موضوع را به عنوان تأییدیه دیگری بر برازش مطلوب مدل در نظر بگیریم.در مدل ما PCLOSE عدد 0.039 حاصل شده است. این موضوع نشان دهنده رد فرض H0 در خصوص برازش مطلوب مدل می‌باشد.

فاصله اطمینان 90% راه دیگری برای ارزیابی برازش مدل بر مبنای RMSE در اختیار ما قرار می‌دهد. حدود اطمینان 90 % یک برآورد فاصله‌ای از RMSE است. چنانچه کران بالایی (HI90) کمتر از 0.05 باشد، این موضوع را به عنوان یک برازش مطلوب از مدل در نظر می‌گیریم. اگر کران بالا بزرگتر از 0.1 باشد، نشان دهنده برازش ضعیف مدل می‌باشد. اگر کران پائین بزرگتر از 0.05 و کران بالایی کوچکتر از 0.1 باشد، نشان دهنده برازش قابل قبول مدل می‌باشد.

ضرایب مسیر استاندارد و غیر استاندارد در تحلیل مسیر

برای مشاهده تخمین‌ها از ضرایب مسیر غیر استاندارد و آزمون‌های معنی‌داری و همچنین تخمین‌های استاندارد مانند شکل زیر روی “Estimates” کلیک کنید.

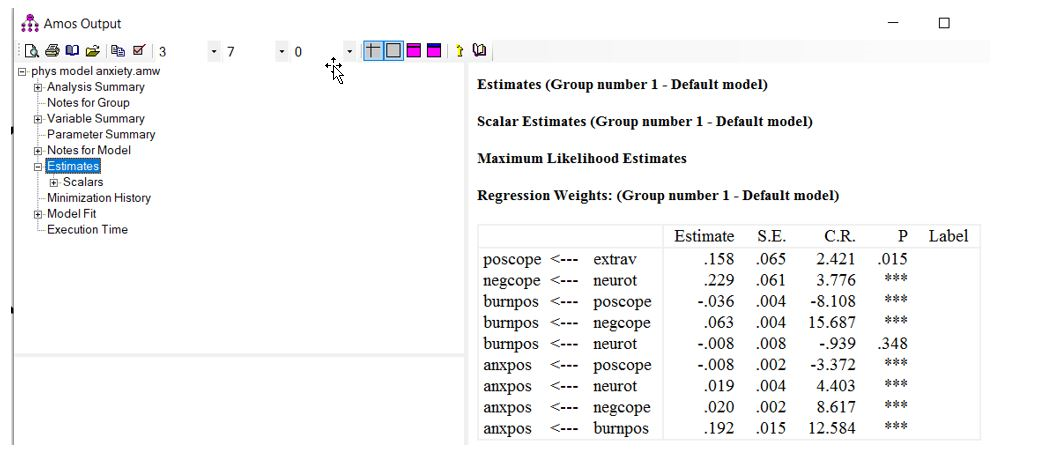
مطابق نتایج در شکل بالا، “Extrav” اثر مثبت و معنی‌دار بر “poscope” دارد (b=0.158، P=0.015). متغیر “neurot” نیز اثر مثبت و معنی‌دار بر “negcope” داشت (b=0.229، P<0.001). میزان اثر و معنی‌داری یا غیر معنی‌داری سایر اثرات را در شکل بالا می‌توانید مشاهده کنید.

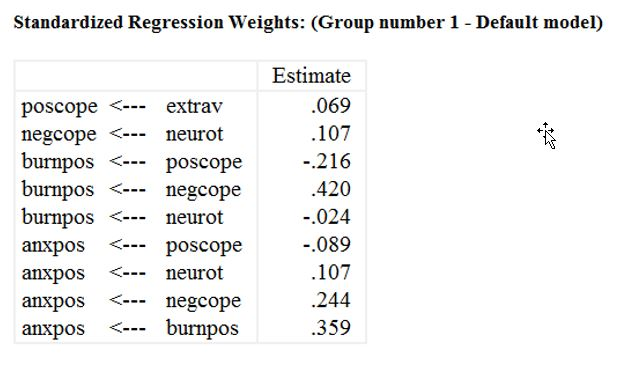
در جدول بالا می‌توانید ضرایب مسیر استاندارد شده را مشاهده کنید. تفسیر این ضرایب همانند ضرایب استاندارد شده در رگرسیون خطی هستند.

جدول بالا کوواریانس‌ها و معنی‌داری آن‌ها را نشان می‌دهد. کوواریانس‌ها برای متغیرهای برون‌زا که با فلش دو جهته در مدل به هم وصل شده‌اند، نشان داده می‌شوند. مقدار کوواریانس بین “Extrav” و “Neurot” منفی و معنی‌دار است (P<0.001).

جدول بالا ضرایب همبستگی (کوواریانس‌های استاندارد شده) را نشان می‌دهد. مطابق نتایج دو متغیر “Extrav” و “Neurot” با هم همبستگی منفی و معنی‌دار دارند (r=-0.367).

در جدول بعد مربع ضرایب همبستگی چند گانه نشان داده شده است. این ضرایب معادل R2 (R-square) هستند. مقادیر R2 برای تمام متغیرهای‌ درون‌زای مدل محاسبه می‌شود.

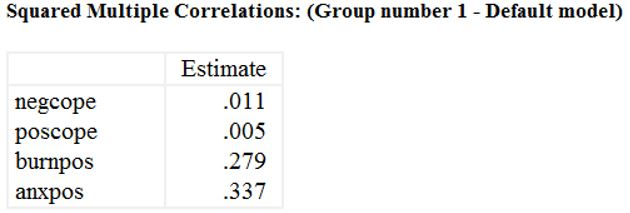
از آنجایی که تنها برون گرایی (extrav) به عنوان پیش بینی کننده مقابله مثبت (poscope) است، می‌توان گفت که تقریباً 0.5 درصد از واریانس مقابله مثبت توسط برون‌گرایی توضیح داده می‌شود. ااز طرف دیگر، فقط روان رنجورخویی (neurot) به عنوان پیش‌بینی‌کننده مقابله منفی (negcope) در مدل وجود دارد، بنابراین تقریباً 1.1 درصد از واریانس مقابله منفی توسط روان رنجور خویی توضیح داده می‌شود. ا

ز آنجایی که فرسودگی شغلی (burnpos) به عنوان پیامد مقابله مثبت، مقابله منفی و روان رنجورخویی مشخص شد، می‌توان گفت که پیش‌بینی‌کننده‌های آن تقریباً 27.9 درصد از واریانس فرسودگی شغلی را تشکیل می‌دهند. در آزمایش ما مقابله مثبت، مقابله منفی، روان رنجورخویی و فرسودگی شغلی همگی پیش‌بینی‌کننده‌های اضطراب (anxpos) بودند، پس می‌توان گفت که این متغیرها به طور مشترک 33.7 درصد از تغییرات اضطراب را تشکیل می‌دهند.

تجزیه‌های اضافی در AMOS

اگر داده‌ها کامل باشند و هیچ داده گم شده‌ای وجود نداشته باشد می‌توانیم تجزیه‌های اضافی زیر را هم انجام دهیم.

در قسمت «Output» می‌توانیم بخش‌های «Residual moments»، «Modification indices»، «Indirect, direct & total effects» و «Tests for normality and outliers» را تیک بزنیم تا در خروجی نتایج آن‌ها را دریافت کنیم.

همچنین می‌توانیم از قسمت «Bootstrap»، بخش‌های «Perform bootstrap»، «Bias-corrected confidence intervals» و «Bootstrap ML» را تیک بزنیم(شکل بالا).

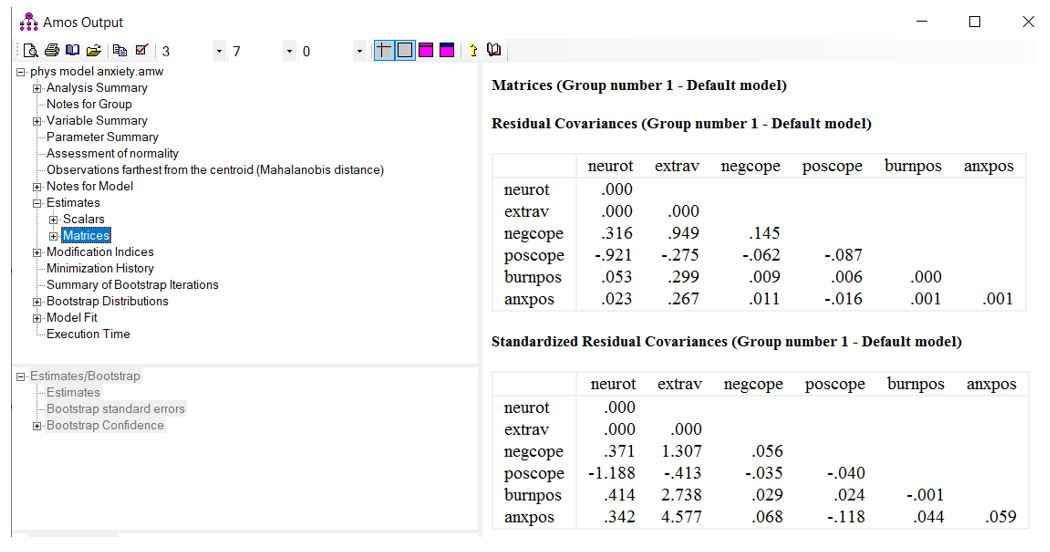
در خروجی نرم افزار از بخش «Matrices» می‌توانیم دو ماتریس کوواریانس باقیمانده‌ها و کوواریانس باقیمانده‌های استاندارد شده را ببینیم (شکل بالا).

این ماتریس‌ها تفاوت بین ماتریس کوواریانس نمونه و ماتریس کوواریانس ضمنی مدل را منعکس می‌کنند. باقیمانده های استاندارد شده «Standardized Residual Covariances» برای شناسایی نقاطی از مدل که برای برازش مشکل ایجاد می‌کنند مفید است. این باقیمانده‌ها مشابه با نمرات استاندارد Z هستند (Byrne , 2010). باقیمانده های بزرگ را می‌توان نشانه‌ای از تعیین نادرست مدل بین دو متغیر در نظر گرفت. محققی به نام Whittaker (2016) باقیمانده‌های بالاتر از 1.96 را “بزرگ” می‌نامد در حالی که Byrne (2010) باقیمانده‌های استاندارد شده بیشتر از 2.58 را به عنوان بزرگ توصیف می‌کند و  پیشنهاد بررسی بیشتر مدل در این نواحی را دارد.

در مدل ما بالاترین باقیمانده های استاندارد شده اعداد 2.738 و 4.577 هستند. هر دو باقیمانده، مشخصات نادرست مدل را نشان می‌دهند. با کلیک بر بخش “Modification indices” می‌توانیم پیشنهادهایی برای برازش بهتر مدل دریافت کنیم (شکل زیر).

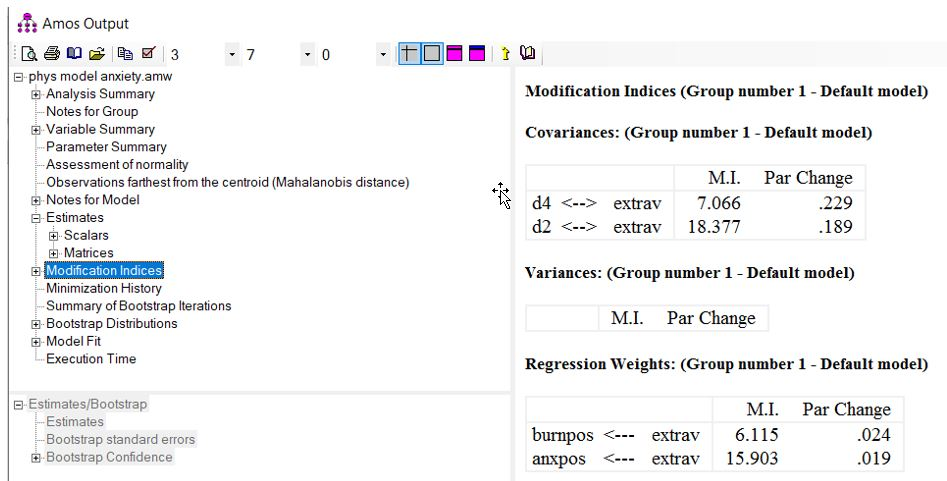
بر اساس بررسی ما از باقیمانده‌های استاندارد شده، شاخص‌های اصلاحی اضافه کردن مسیری از برون گرایی به فرسودگی شغلی و از برون گرایی به اضطراب را پیشنهاد می‌دهد.

نکته: استفاده از ماتریس‌های باقی‌مانده و شاخص‌های اصلاح، استراتژی‌های تجربی هستند که منابع تشخیص نادرست مدل را مشخص می‌کنند. این استراتژی‌ها هنگام تصمیم‌گیری در مورد اینکه چگونه مدل خود را مجدداً بازسازی کنید، مورد توجه قرار می‌گیرند. توجه داشته باشید که صرفاً تکیه بر معیارهای تجربی برای تصمیم‌گیری در مورد تعیین مجدد مدل می‌تواند شما را به سمت مدلی سوق دهد که با داده‌های شما بهتر از مدل اصلی شما مطابقت داشته باشد، اما الزاما همان برازش مدل در سایر نمونه‌های جمعیت به دست نخواهد آمد. به همین دلیل، بسیار مهم است که در هر گونه تعریف مجدد مدل بر اساس معیارهای تجربی عاقلانه رفتار کنید و مطمئن شوید که هر تغییری که ایجاد می کنید منطقی و صحیح است.

آزمون نرمال بودن داده‌ها در تحلیل مسیر

یک فرض کلیدی هنگام انجام تحلیل مسیر با تخمین حداکثر درستنمایی (ML) این است که متغیرهای (و به ویژه، متغیرهای درون زا) مدل دارای توزیع نرمال چند متغیره باشند. هنگامی که فرض نرمال بودن چند متغیره نقض می شود، می‌تواند منجر به یک مقدار کای‌دو متورم شود که باعث برازش غیر مطلوب بر داده ها می‌شود. از سوی دیگر، غیر نرمال بودن داده‌ها می‌تواند منجر به خطاهای استانداردی شود که به سمت پایین هدایت می‌شوند و به طور بالقوه ریسک خطای نوع I را هنگام آزمایش پارامترهای مدل افزایش می‌دهند. بنابراین باید هنگام برازش مدل، نرمال بودن متغیرها را نیز مورد بررسی قرار داد.

با کلیک بر بخش «Assessment of normality» می‌توانیم شاخص‌هایی را برای نرمال بودن داده‌ها مشاهده کنیم (شکل زیر).

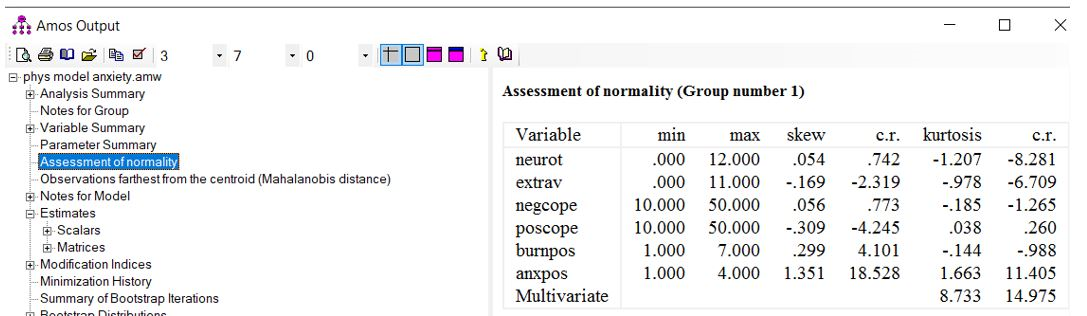
در این بخش از خروجی، ما دو کمیت چولگی (skew) و کشیدگی (kurtosis) را برای هر متغیر در مدل داریم. اینها برای قضاوت در مورد اینکه آیا شواهدی مبنی بر انحراف از نرمال بودن تک متغیره وجود دارد مفید هستند. به خاطر داشته باشید که نرمال بودن تک متغیره شرط لازم برای نرمال بودن چند متغیره است. اما نرمال بودن تک متغیره شرط کافی برای نرمال بودن چند متغیره نیست. بنابراین، شاخص کشش چند متغیره (Multivariate) در پایین این جدول ارائه شده است تا قضاوت شما را در مورد غیر نرمال بودن چند متغیره تسهیل کند.

از مقادیر (skew) و (kurtosis) برای ارزیابی نرمال بودن تک متغیره استفاده می‌شود. ستون‌ (cr) حاوی مقادیر z است. از این ستون برای آزمایش اینکه آیا توزیع تک متغیره به طور معنی‌داری از نرمال بودن با توجه به چولگی یا کشیدگی فاصله می‌گیرد یا خیر استفاده می‌شود. (توجه: این نتایج تحت تأثیر حجم نمونه است و ممکن است به ویژه در نمونه های بسیار بزرگ مفید نباشد). بطور سر انگشتی، مقادیر چولگی بین 2- و 2+ با نرمال بودن توزیع سازگار است. در حالی که مقادیر > 3 (در مقدار مطلق) نشان دهنده غیر نرمال بودن توزیع است.

برای شاخص کشیدگی قانون کلی وجود ندارد. با این حال Lomax و Hahs -Vaughn (2012) مقادیر بین 2- و 2+ را با نرمال بودن پیشنهاد می کنند. اما Byrne (2010) مقادیر 7 یا 8 و بیشتر از آن را به عنوان معیاری از نرمال نبودن متغیرها در شاخص کشیدگی مطرح می‌کند.

نرمال بودن توزیع را می‌توانیم از طریق روش‌های گرفیکی مانند رسم هسیتوگرام و P-P پلات نیز بررسی کنیم.

در آزمایش ما به نظر می‌رسد که مقادیر چولگی و کشیدگی برای متغیرها شواهدی برای نرمال بودن تک متغیره ارائه می‌دهد.

نرمال بودن چند متغیره

نرمال بودن چند متغیره در آموس از طریق شاخص کشیدگی چند متغیره ماردیا (Mardia’s index) سنجش می‌شود. بر اساس گفته Bentler (2005) و Byrne (2010) مقدار کشیدکی چند متغیره <5 نشان دهنده غیر نرمال بودن توزیع چند متغیره است. در مثال ما هم مقدار کشیدگی چند متغیره 8.733 است که بزرگتر از 5 می‌باشد و نشان دهنده غیر نرمال بودن توزیع چند متغیره می‌باشد.

کمیت cr در شاخص ماردیا معادل مقدار Z می‌باشد. چنانچه بخواهیم تفاوت انحراف توزیع متغیرها را نسبت به توزیع نرمال چند متغیره در سطح پنج درصد سنجش کنیم، آستانه 1.96 را به عنوان معیار معنی‌داری در نظر می‌گیریم. طبق این آستانه، برای شاخص ماردیا مقدار Z برابر با 14.975 دارد. بنابراین نتیجه می‌گیریم که توزیع چندمتغیره متغیرهای ما بطور معنی‌داری از توزیع نرمال چند متغیره فاصله دارد.

Refrences

Byrne, B. M. (2010). Structural equation modeling with AMOS: Basic concepts, applications, and programming (2nd ed.). New York: Routledge.

International Personality Item Pool: A Scientific Collaboratory for the Development of Advanced Measures of Personality Traits and Other Individual Differences (http://ipip.ori.org/). Internet Web Site.

Kline, R. B. (2016). Principles and practice of structural equation modeling (4th ed.). New York: The Guilford Press.

Lomax, R. G., & Hahs-Vaughn, D. L. (2012). An introduction to statistical concepts (3rd ed.). New York: Routledge.

Pituch, K. A., & Stevens, J. P. (2016). Applied Multivariate Statistics for the Social Sciences (6th ed.). New York: Routledge.

Schumacker, R. E., & Lomax, R. G. (2016). A beginner’s guide to structural equation modeling (4th ed.). New York: Routledge.

Tabachnick, B. G., & Fidell, L. S. (2013). Using multivariate statistics (6th edition). Pearson: Street, Upper Saddle River, New Jersey.

Whittaker, T. A. (2016). ‘Structural equation modeling’. Applied Multivariate Statistics for the Social Sciences (6th ed.). Routledge: New York. 639-746.