همبستگی (قسمت دوم: آزمون فرضیات، پیش‌فر‌ض‌ها)

در این مقاله در مورد آزمون فرضیات همبستگی و پیش‌فرض‌های آن صحبت می‌کنیم. این مقاله دومین قسمت از مقالات مربوط به همبستگی است. لطفاً قبل از مطالعه، بخش اول را مطالعه نمایید.

آزمون فرضیات همبستگی

برای همبستگی می‌توانیم فرضیات یکطرفه یا دو طرفه تعیین کنیم. به آزمون فرض زیر  دقت کنید:

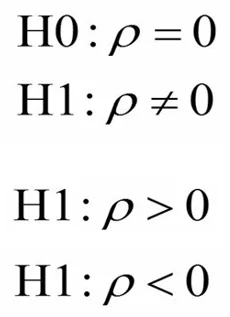
فرض صفر ب گزاره‌ای است که بیان می‌کند ضریب همبستگی برابر با صفر است. یعنی بین دو متغیر هیچ رابطه‌ای وجود ندارد.

در صورتی که آزمون دو طرفه باشد: فرض مخالف (H1) بیان می‌کند که ضریب همبستگی برابر با صفر نیست.

زمان که آزمون ما یکطرفه باشد فرض مخالف (H1) بیان می‌کند که ضریب همبستگی بزرگتر  یا کوچکتر از صفر است.

آزمون ضریب همبستگی

برای آزمون ضریب همبستگی از توزیع تی استفاده می‌کنیم. فرمول محاسبه مقدار تی به شرح زیر است:

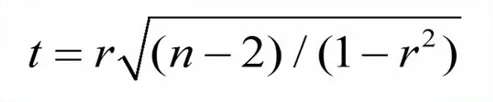
در این فرمول r ضریب همبستگی نمونه و n حجم نمونه را نشان می‌دهد.

مثال

فرض کنید وزن و قد 6 نفر را اندازه‌گیری کرده‌ایم. وزن و قد این افراد را می‌توان در در قالب یک تمودار پراکنش نشان داد (شکل 1).

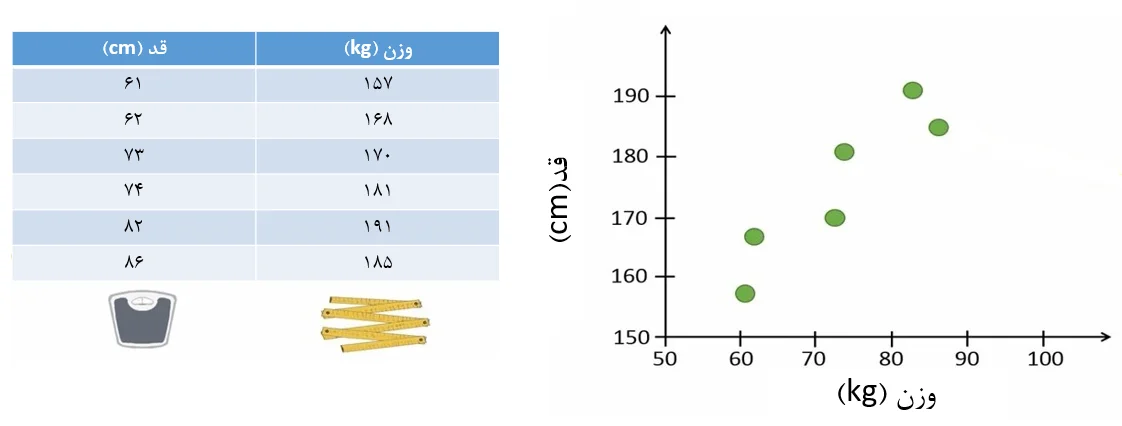
شکل 1. وزن و قد شش نفر و رسم نمودار پراکنش برای آن‌ها

در مقاله قبل میانگین و انحراف استاندارد وزن این 6 نفر را محاسبه کردیم که به شرح زیر است:

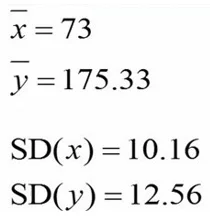
با استفاده از مقادیر میانگین و انحراف معیار، کوواریانس دو متغیر را به شرح زیر محاسبه می‌کنیم:

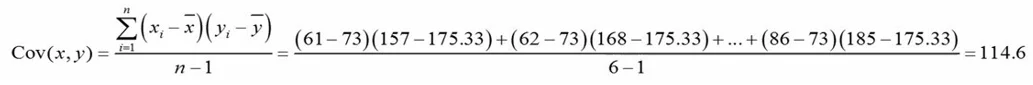
نهایتاً مقدار کوواریانس را در صورت کسر   و انحراف معیار دو متغیر را در مخرج کسر قرار می‌دهیم:

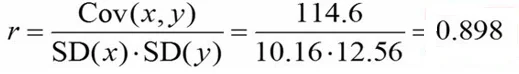
همانطور که ملاحظه می‌کنید، ضریب همبستگی پیرسون را 0.898 بدست آورده‌ایم.

محاسبه آماره تی

حالا می‌توانیم ضریب همبستگی و حجم نمونه را در فرمول قرار دهیم و آماره تی را محاسبه کنیم.

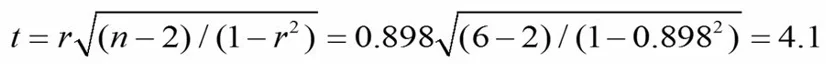
در این مثال آماره تی را 4.1 بدست آورده‌ایم. پس باید از توزیع تی با درجه آزادی n-2 استفاده کنیم. چون در محاسباتمان دو مقدار میانگین تخمین زده‌ایم، درجه آزادی برابر با شش منهای دو است.

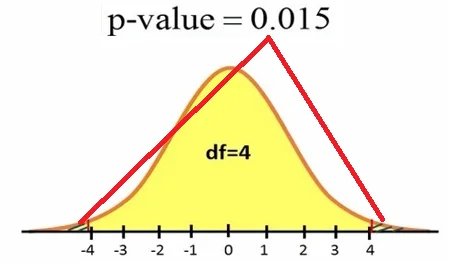
شکل 2. توزیع تی با درجه آزادی 4

با استفاده از یک نرم افزار آماری می‌توانیم سطح زیر نمودار سمت راست مقدار تی 4.1 و سمت چپ مقدار تی 4.1- را محاسبه کنیم (شکل 2). این مقدار P-value‌ است که در این مثال 0.015 بدست آورده‌ایم.

چون مقدار P-value کوچکتر از سطح خطای در نظر گرفته شده (0.05) است، فرض صفر (H0) رد می‌کنیم و نتیجه می‌گیریم که ضریب همبستگی بطور معنی‌داری با صفر متفاوت است. چون علامت ضریب همبستگی مثبت است، ارتباط بین دو متغیر همسو است و با افزایش یکی، دیگری هم افزایش می‌یابد.

نکته مهم در مورد ضریب همبستگی

معنی‌داری رابطه بستگی به دو فاکتور مقدار ضریب همبستگی و حجم نمونه دارد. هر چه مقدار تی بزرگتر باشد، مقدار P-value کاهش می یابد. پس همبستگی‌های نزدیک به عدد 1+ یا 1- مقدار P-value کوچکتری می‌دهند. اما با توجه به فرمول آزمون تی، هر چه حجم نمونه هم بیشتر باشد، مقدار P-value کوچکتر خواهد بود.

در مثال ما، تعداد داده‌ها کم بود. اما ضریب همبستگی به حدی بزرگ بود که بتواند کم بودن حجم نمونه را پوشش دهد و معنی‌دار شود. اما اگر رابطه ضعیف بین دو متغیر برقرار باشد، باید حجم نمونه بالا باشد تا بتوانیم فرض H0 را رد کنیم. مثلاً اگر با همین تعداد داده، همبستگی 0.2 بدست می‌آمد، مقدار P-value بزرگتر از 0.05 می‌شد و نمی‌توانستیم فرض H0 را رد کنیم.

تفسیر حدود اطمینان

فرض کنید حدود اطمینان 95 درصد را برای یک ضریب همبستگی بازه 0.2- تا 0.4 بدست آورده‌ایم.

این حدود اطمینان نشان می‌دهد که 95 درصد اطمینان داریم که ضریب همبستگی بین دو متغیر، در بازه 0.2- تا 0.4 است. چون این حدود اطمینان عدد صفر را در بر می‌گیرد، می‌توانیم نتیجه بگیریم که ضریب همبستگی ما با صفر تفاوت معنی‌دار ندارد.

پیش‌فرض‌های همبستگی

در این بخش پیش فرض‌های همبستگی را با هم بررسی می‌کنیم.

• اولین مفروض، استقلال مقادیر است. استقلال مقادیر یعنی هیچ نوع ارتباطی بین واحدهای آزمایشی یا افراد در آزمایش نباید وجود داشته باشد.
• دومین مفروض این است که باید بین دو متغیر رابطه خطی وجود داشته باشد. اگر در نمودار پراکنش داده‌ها ارتباط درجه دوم یا نمایی یا هر نوع ارتباط دیگری غیر از رابطه مشاهده کنیم، دیگر نمی‌توانیم از ضریب همبستگی برای سنجش ارتباط دو متغیر استفاده کنیم.
• هر دو متغیر باید مقیاس پیوسته و توزیع نرمال داشته باشند. ضریب همبستگی پیرسون به اعداد پرت و دورافتاده خیلی حساس است. پس اگر در مقادیر ما اعداد پرت یا دورافتاده وجود داشت، نباید از این ضریب برای سنجش رابطه استفاده کرد. در این مواقع از ضریب همبستگی اسپیرمن  استفاده می‌کنیم.