آشنایی با حدود اطمینان

در این مقاله در مورد حدود اطمینان میانگین صحبت می‌کنیم.

حدود اطمینان می‌تواند برای دو حالت مختلف محاسبه شود.

• زمانی که نمونه ما بزرگ است یا انحراف استاندارد جامعه مشخص است.
• زمانی که نمونه ما کوچک است یا انحراف استاندارد جامعه مشخص نیست.

در این جلسه ما حدود اطمینان را زمانی که انحراف استاندارد جامعه مشخص است، محاسبه می‌کنیم. در جلسه جداگانه دیگری حدود اطمینان را با استفاده از توزیع تی،  زمانی که نمونه ما کوچک است محاسبه کرده‌ایم.

خطای استاندارد میانگین

برای محاسبه حدود اطمینان، باید با مفهوم خطای استاندارد میانگین و نحوه محاسبه آن آشنا باشید. قبلاً در قالب یک جلسه این مفهوم را بطور کامل بررسی کرده‌ایم.

فرمول خطای استاندارد میانگین به شرح زیر است.

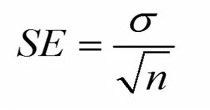
در این فرمول سیکما انحراف استاندارد جمعیت و n حجم نمونه را نشان می‌دهد.

نحوه محاسبه حدود اطمینان میانگین

فرض کنید می‌خواهیم میانگین قد افراد یک جمعیت را تخمین بزنیم. در حالی‌که انحراف استاندارد قد افراد این جمعیت را می‌دانیم (شکل 1). فرض کنید انحراف استاندارد جمعیت ما 10 باشد (البته درمثال‌های واقعی اغلب ما هیچ اطلاعی از انحراف استاندارد جمعیت نداریم).

شکل 1. توزیع قد افراد جمعیت

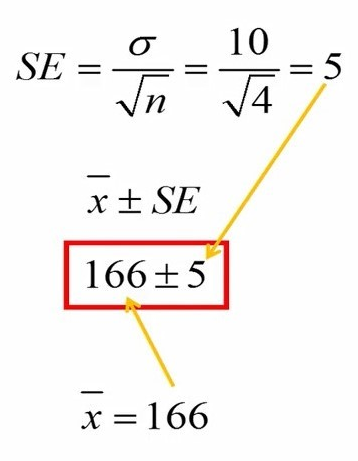
برای تخمین میانگین قد، یک نمونه چهار نفری از افراد این جمعیت اخذ می‌کنیم. مثلاً میانگین نمونه 166 بدست می‌آید. چون از قبل انحراف استاندارد جمعیت را می‌دانیم، می‌توانیم مقدار میانگین و انحراف استاندارد را در فرمول قرار دهیم و مقدار خطای استاندارد را بدست آوریم. مطابق شکل 2، خطای استاندارد میانگین را 5 بدست آورده‌ایم.

شکل 2. اخذ نمونه از جمعیت و محاسبه میانگین و خطای استاندارد

اگر ما میانگین را به علاوه منهای خطای استاندارد کنیم یک بازه بدست می‌آید که حدود اطمینان نام دارد (شکل 3).

برای این مثال حدود اطمینان 161 تا 171 بدست آمد که به ما می‌گوید در مورد میانگین‌های برآورد شده چقدر اطمینان داریم. در مورد این مثال می‌توانیم بگوییم 68 درصد اطمینان داریم که میانگین حقیقی جامعه در بازه اطمینان قرار دارد. بنابراین خطای استاندارد، نصف عرض محدوده‌ای را نشان می‌دهد که 68% میانگین‌ها در آن قرار دارند. اگر نمی‌دانید عدد 68 از کجا آمده است مقاله مربوط به خطای استاندارد را ببینید.

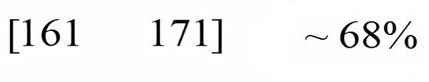
حدود اطمینان 95 درصد

در آمار اغلب باید در مورد تخمین‌های جمعیت 95 درصد اطمینان داشته باشیم. از جلسه مربوط به توزیع نرمال به خاطر داریم که اگر ما به اندازه‌ 1.96 واحد از دو طرف میانگین در توزیع نرمال استاندارد فاصله بگیریم، 95 درصد از توزیع نرمال استاندارد را پوشش داده‌ایم (شکل 4).

شکل 4. بازه اطمینان 95 درصد در توزیع نرمال استاندارد

برای تغییر حدود اطمینان 68 درصد به 95 درصد ما خطای استاندارد را در 1.96 ضرب کنیم. در اینصورت حد پائین و بالا به ترتیب  154.2 و 173.8 بدست می‌آید. واضح است که فاصله اطمینان 68%، کوچکتر از فاصله اطمینان 95% است.

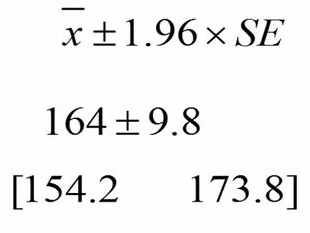
محاسبه بازه اطمینان 95 درصد با استفاده از چند نمونه متفاوت

به عنوان مثال اگر از همین جامعه بطور تصادفی 100 نمونه 4 تایی بگیریم، 100 حدود اطمینان می‌توانیم محاسبه کنیم. حالا انتظار داریم 95 تا از این حدود اطمینان‌‌ها شامل میانگین حقیقی جامعه باشند و تنها 5 درصد این محدوده ها شامل میانگین حقیقی جامعه نباشند. اگر به شکل 5 دقت کنید،‌ محدوده اطمینانی که با استفاده از آخرین نمونه ما از جمعیت بدست آمد، شامل میانگین حقیقی جامعه نیست.

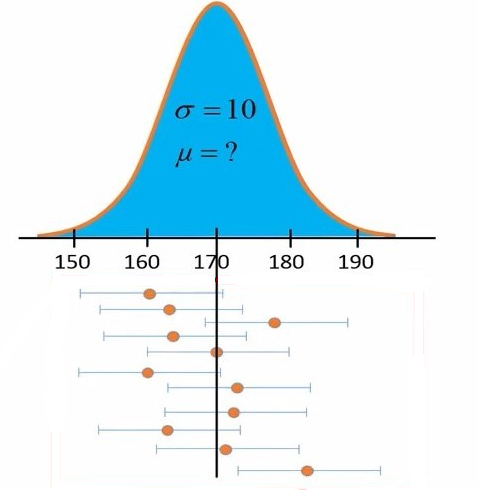
شکل 5. نمایش بازه اطمینان 95 درصد از چند نمونه با حجم 4

توجه کنید که ما در واقعیت، میانگین حقیقی جامعه را نمی‌دانیم. پس هرگر نمی‌دانیم که حدود اطمینان 95 % که بدست آورده‌ایم شامل میانگین حقیقی جمعیت هست یا خیر؟ اما می‌توانیم 95 % اطمینان داشته باشیم که محدوده ما شامل میانگین حقیقی جمعیت است.

تأثیر حجم نمونه در حدود اطمینان

در مثال قبل ما از نمونه‌های چهار نفری استفاده کردیم. چون حجم نمونه‌های ما کم بود، حدود اطمینان 95 % نسبتاً عریض بدست آمد.

فرض کنید  حجم نمونه را به 100 افزایش دهیم. در اینصورت خطای استاندارد ما از 5 به 1 کاهش می‌یابد. در این صورت حدود‌های اطمینان  باریک‌تر خواهد شد و تمرکز بیشتری در اطراف میانگین پیدا می‌کنند. با وجود این، هنوز ما انتظار داریم که 95 درصد حدود‌های اطمینان شامل میانگین حقیقی جامعه باشند (شکل 6).

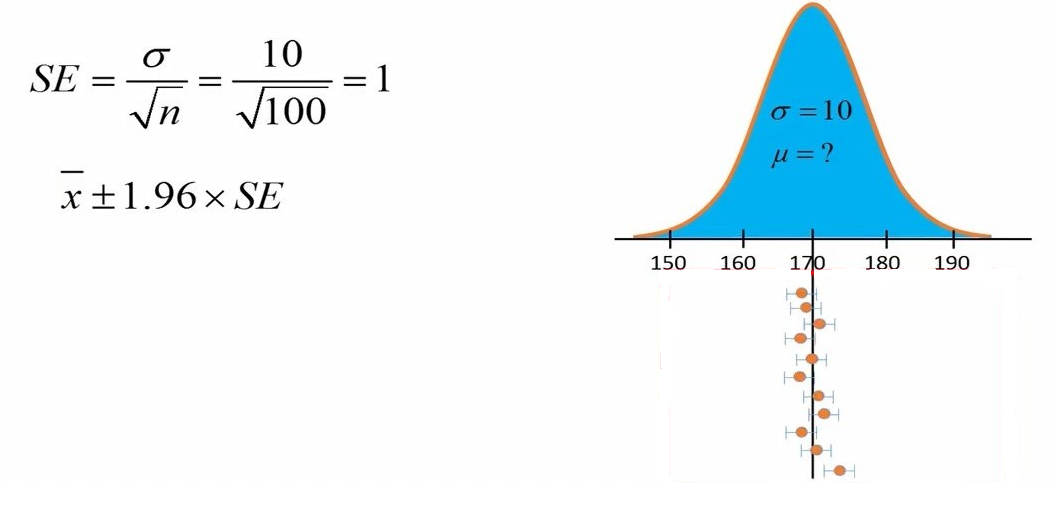
شکل 6. نمایش بازه اطمینان 95 درصد از چند نمونه با حجم 10