رگرسیون خطی (قسمت اول: مفهوم)

در این مقاله  مفهوم رگرسیون خطی را با مثال بررسی می‌کنیم.

مثال در مورد رگرسیون خطی

فرض کنید می‌خواهیم خودرو خودمان را بفروشیم. خودرو ما 3 سال سن دارد و نمی‌دانیم باید با چه قیمتی آن را بفروشیم. برای اینکه بدانیم خودرو چه ارزشی دارد قیمت 6 خودرو مشابه را از بازار استعلام می‌کنیم.

قیمت و سن 6 خودرو را در شکل 1 آورده‌ایم.

شکل 1. قیمت و سن 6 خودرو

یک راه برای فهمیدن قیمت خودرو این است که قیمت را مشابه با خودروی هم سن خودرو خودمان انتخاب کنیم. در شکل 1، یک خودرو وجود دارد که 3 سال سن دارد و 18 هزار یورو قیمت دارد. پس ما می‌توانیم قیمت خودرو خودمان را نیز 18 هزار یورو تعیین کنیم.

اما آیا راهی وجود دارد که قیمت خودرو خودمان را بر مبنای قیمت تمام خودروهای شکل 1 مشخص کنیم؟ با استفاده از رگرسیون خطی می‌توانیم این کار را انجام دهیم.

رسم نمودار پراکنش و تخمین قیمت خودرو

اگر دو متغیر قیمت و سن خودرو را در قالب یک نمودار پراکنش نشان دهیم، می‌توانیم یک خط از بین نقاط عبور دهیم و با استفاده از آن، از روی سن خودرو، قیمت را پیش‌بینی کنیم.

برای این کار متغیری که می‌خواهیم پیش‌بینی کنیم را روی محور Y قرار می‌دهیم و متغیری که می‌خواهیم با آن پیش‌بینی را انجام دهیم روی محور X قرار می‌دهیم و نمودار پراکنش را رسم می‌کنیم (شکل 2).

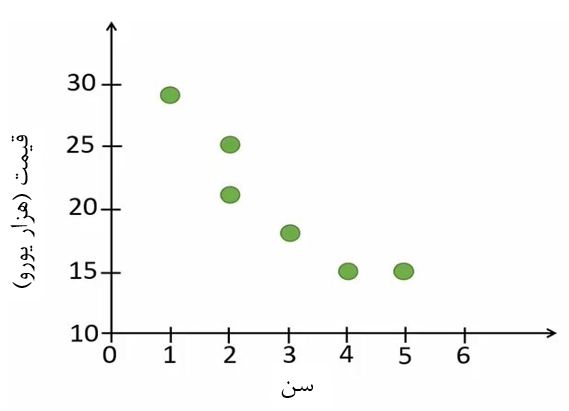
شکل 2. نمودار پراکنش سن و قیمت خودرو

حالا می‌توانیم از بین نقاط روی نمودار پراکنش بهترین خط را عبور دهیم بطوریکه فاصله نقاط از خط کمترین مقدار ممکن را داشته باشد. زمانی که این خط را رسم کردیم می‌توانیم از آن برای پیش‌بینی قیمت خودرو استفاده کنیم (شکل 3).

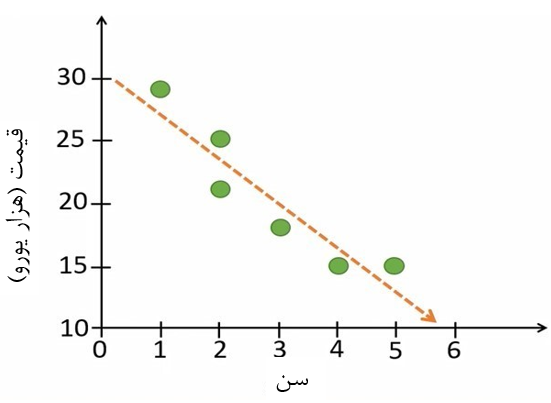
شکل 3. برازش بهترین خط از بین نقاط نمودار پراکنش

چون خودروی ما 3 سال سن دارد، از محور سن یک خط عمودی روی خط رگرسیون رسم می‌کنیم و بعد از خط رگرسیون یک خطی افقی روی محور قیمت رسم می‌کنیم تا قیمت خودرو را بدست آوریم (شکل 4).

شکل 4. تخمین قیمت خودرو از روی سن خودرو

همانطور که ملاحظه می‌کنید، قیمت خودرو ما حدود 20 هزار یورو بدست می‌آید. با همین روش می‌توانیم قیمت خودروهای با سنین مختلف را محاسبه کنیم.

معادله خط رگرسیون

روش بهتر برای تخمین قیمت خودرو این است که از معادله خط رگرسیون برای تخمین قیمت استفاده کنیم. معادله خط رگرسیون به شرح زیر است:

تفسیر اجزای معادله رگرسیون خطی

در معادله خط دو پارامتر را تخمین می‌زنیم. پارامتر اول یک مقدار ثابت است که عرض از مبدأ نام دارد. دومین پارامتر شیب خط نامیده می‌شود. در مثال ما، عرض از مبدأ 30.57 و شیب 3.57- بدست آمد.

عرض از مبدأ، نقطه تقاطع خط رگرسیون با محور Y است. یعنی اگر X صفر باشد، مقدار Y چقدر خواهد بود. برای این مثال عرض از مبدأ، قیمت خودروهای صفر را تخمین می‌زند. پس ما تخمین می‌زنیم که خودروی نو، 30.57 هزار یورو قیمت دارد.

علامت شیب خط نوع رابطه دو متغیر را نشان می‌دهد. بطوریکه اگر علامت منفی باشد رابطه معکوس و اگر علامت مثبت باشد، رابطه مستقیم است. چون در این مثال علامت شیب خط منفی است، نشان می‌دهد که با افزایش سن خودرو قیمت کاهش می‌یابد.

مقدار شیب خط 3.55- است که نشان می‌دهد به ازای افزایش یک سال سن خودرو، قیمت خودرو 3.55 هزار یورو کاهش می‌یابد.

تخمین قیمت خودرو با استفاده از معادله رگرسیون خطی

برای تخمین قیمت خودرو باید سن خودرو را در معادله خط رگرسیون قرار دهیم. تخمین قیمت یک خودرو با سه سال کارکرد به شرح زیر است:

با استفاده از معادله خط رگرسیون، قیمت خودروی 3 سال کارکرد را 19.92 تخمین زدیم. از طریق معادله خط رگرسیون، برای هر سنی از خودروها می‌توانیم قیمت را تخمین بزنیم.

نکته مهم: تخمین‌های ما فقط در محدوده سنی که معادله خط را بدست آوردیم معتبر است. در خارج از بازه، تخمین‌ها باید با احتیاط انجام شود.

برای فهم این موضوع به شکل 5 دقت کنید. قیمت خودرویی که 8.5 سال سن دارد، بر مبنای معادله خط رگرسیون تقریباً برابر با صفر می‌شود. اما می‌دانیم که این موضوع صحیح نیست.

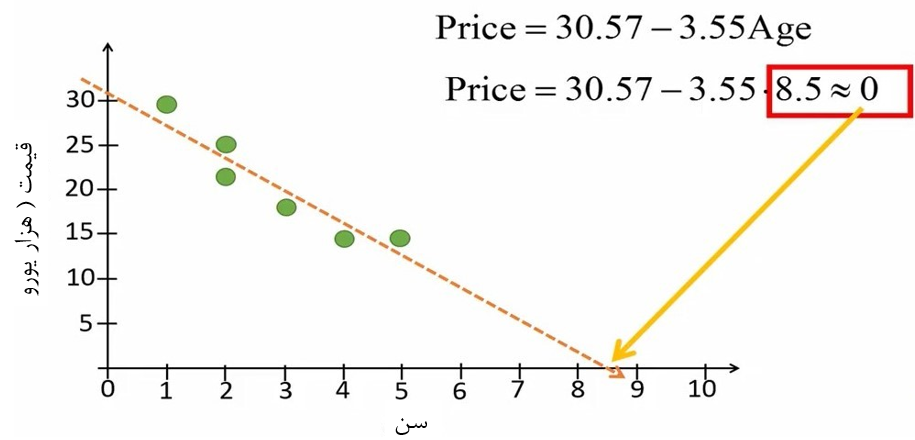
شکل 5. تخمین قیمت خودرو در خارج از بازه خط رگرسیون

به نظر می‌رسد که خط رگرسیون ما برای خودروهای تا 6 سال کارکرد صحیح باشد و برای خودروهای با کارکرد بالاتر باید مدل دیگری برازش کنیم.

مدل نمایی

فرض کنید نمودار پراکنش داده‌ها مانند شکل 6 باشد.

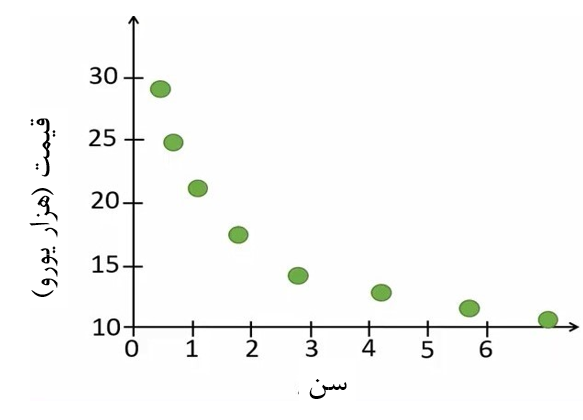
شکل 6. داده‌ها با مدل نمایی

در این حالت چون بین دو متغیر ارتباط خطی برقرار نیست، برازش یک خط مستقیم بین این داده‌ها مناسب نیست. بنابراین باید از رگرسیون‌های غیر خطی مانند شکل 7 برای اینطور داده‌ها استفاده کنیم.

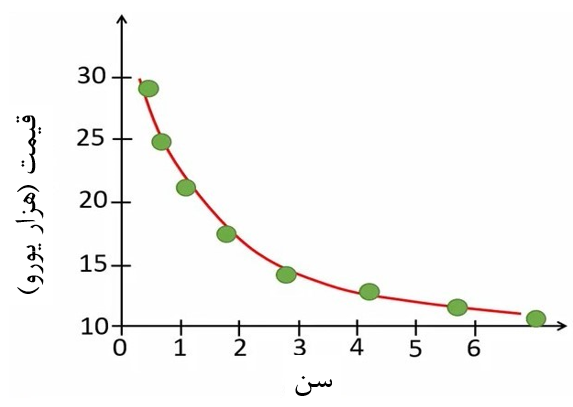
شکل 7. برازش مدل نمایی بر داده‌ها

سایر متغیرها در رگرسیون خطی

سؤالی که اینجا پیش می‌آید این است که آیا قیمت خودرو فقط به سن مرتبط است؟

مشخص است که قیمت خودرو به انواع مختلفی از متغیرهای دیگر از جمله کارکرد، نوع موتور، آپشن‌ها و سایر شرایط بستگی دارد. به عواملی که در مدل رگرسیون در نظر نگرفته‌ایم، اثرات تصادفی (Random effects) می‌گوییم.

به شکل 8 دقت کنید. در نمودار پراکنش دور دو نقطه مستطیل قرمز کشیده‌ایم. این دو خودرو سن مشابهی دارند، اما قیمت آن‌ها 4 هزار یورو با هم متفاوت است. دلیل اینکه این دو خودرو با اینکه سن مشابه دارند، قیمت متفاوت دارند اثرات تصادفی است که ما در مدل در نظر نگرفته‌ایم.

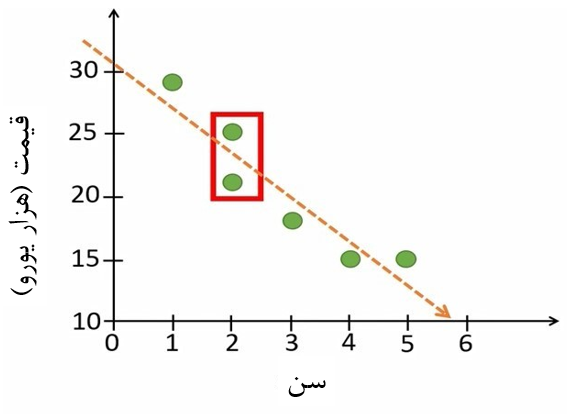
شکل 8. دو خودرو با سن مشابه و قیمت متفاوت

برای اینکه بتوانیم قیمت خودروها را بهتر پیش بینی کنیم، می‌توانیم غیراز سن خودرو اطلاعات بیشتری برای هر خودرو جمع‌آوری کنیم. مثلاً می‌توانیم کیلومتر کارکرد و نوع موتور را نیز مشخص کنیم. این متغیرها نیز می‌توانند در داخل مدل رگرسیونی قرار گیرند.

زمانی که ما در یک مدل رگرسیونی بیشتر از یک متغیر استفاده می‌کنیم، رگرسیون خطی چند گانه داریم که در یک مقاله جداگانه به آن می پردازیم.

اصطلاحات رگرسیون خطی

به مدل رگرسیون زیر دقت کنید:

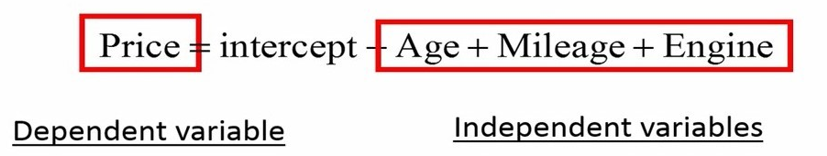
به متغیری که در مدل تخمین زده می‌شود، متغیر وابسته (Dependent variable) یا متغیر پاسخ (response variable) می‌گوییم. در مدل ما قیمت، یک متغیر وابسته است. متغیر یا متغیرهایی که در سمت راست معادله رگرسیون قرار می‌گیرند را متغیرهای مستقل (independent variable) یا توضیحی (explanatory variable) می‌نامیم.

توجه کنید که در رگرسیون، متغیر وابسته باید عددی و پیوسته باشد. اما متغیرهای مستقل می‌توانند مقیاس عددی یا طبقه‌ای داشته باشند. اگر با انواع متغیرها آشنا نیستید، می‌توانید به مقاله مربوطه مراجعه کنید.

در مدل رگرسیونی ما متغیرهای سن و کارکرد خودرو از نوع عددی و متغیر نوع موتور از نوع طبقه‌ای است.

مثال عددی برای رگرسیون خطی

فرض کنید سن و میزان فشار خون سیستولیک 7 فرد را اندازه‌گیری کرده‌ایم (شکل 1).

شکل 9. سن و میزان فشار خون 7 فرد

در این مثال می‌خواهیم فشار خون را بر مبنای سن افراد پیش‌بینی کنیم. بنابراین فشار خون را روی محور عمودی(Y) و سن را روی محور افقی (X) قرار می‌دهیم (شکل 10).

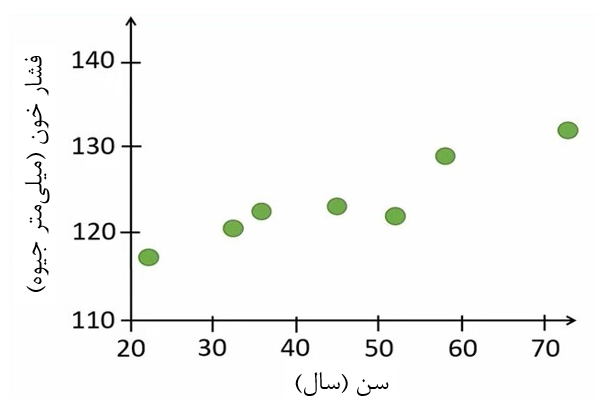
شکل 10. نمودار پراکنش سن و فشار خون

فشار خون متغیر وابسته و سن متغیر مستقل است. در واقع ما تلاش می‌کنیم که تغییرات فشار خون را با استفاده از سن افراد توضیح دهیم.

حالا می‌توانیم بر داده‌ها یک خط رگرسیونی برازش کنیم. خط را باید طوری از بین نقاط عبور دهیم که نقاط ما کمترین فاصله عمودی را نسبت به خط داشته‌ باشند (شکل 11). نحوه برازش خط را در مقاله دیگری بطور مفصل بررسی می‌‌کنیم.

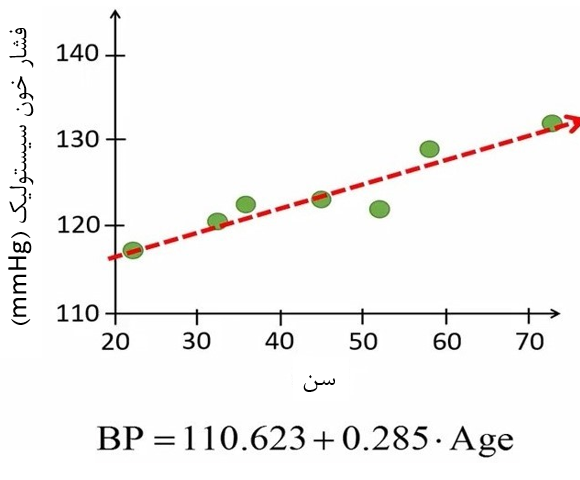
شکل 11. برازش خط رگرسیونی بر داده‌ها

در این پژوهش، مقدار عرض از مبدأ را 110.623 بدست آورده‌ایم. این موضوع نشان می‌دهد که افراد تازه متولد شده فشار خون 110.623 دارند. نکته‌ای باید توجه کنیم این است که محور افقی ما از عدد 20 شروع می‌شود و ما اطلاعات افراد زیر 20 سال را اندازه‌گیری نکرده‌ایم. بنابراین خط رگرسیونی فقط برای افراد بالای 20 سال معتبر است. چون عرض از مبدأ خارج از محدوده خط رگرسیونی است، تخمین فشار خون برای افراد تازه متولد شده ممکن است صحیح نباشد.

شیب خط رگرسیون به ما نشان می‌دهد که با افزایش یک سال سن، 0.285 میلی متر جیوه فشار خون افراد افزایش می‌یابد.

اما سؤال اصلی این آزمایش این است که شیب خط چقدر باشد تا ما بگوییم بین سن و فشار خون رابطه وجود دارد؟ این سؤال را در مقاله دوم از مبحث رگرسیون پاسخ خواهیم داد.