همبستگی (قسمت اول: مفهوم، ضریب همبستگی پیرسون)
در این مقاله در مورد مفهوم همبستگی (correlation) صحبت میکنیم.
ما مبحث همبستگی را در طی سه مقاله بطور کامل بررسی میکنیم. در این مقاله مفهوم و ضریب همبستگی پیرسون را یاد میگیریم. آزمون فرضیات و پیشفرضهای همبستگی را در مقاله دوم بررسی میکنیم. در مقاله سوم در مورد ضریب همبستگی رتبهای اسپیرمن صحبت میکنیم.
مثال برای مفهوم همبستگی
فرض کنید وزن و قد شش نفر را اندازهگیری کردهایم. وزن و قد این افراد را میتوان در در قالب یک نمودار پراکنش مانند شکل 1 نشان داد.

شکل 1. وزن و قد شش نفر و رسم نمودار پراکنش برای آنها
الان میتوانیم یک خط بهینه از بین نقاط عبور دهیم. بطوریکه نقاط کمترین فاصله عمودی را نسبت خط داشته باشند. به شکل 2 دقت کنید. نقاط از سمت چپ به راست نمودار به سمت بالا حرکت میکنند. بنابراین ما در این نمودار شیب مثبت داریم. زمانی که شیب مثبت داریم، میگوییم دو متغیر در نمودار پراکنش همجهت و دارای رابطه مثبت هستند. رابطه مثبت یعنی وقتی یک متغیر افزایش مییابد، متغیر دیگر هم افزایش یابد.

شکل 2. برازش خط از بین نقاط در اطلاعات وزن و قد افراد
حالا مثال دیگری را در نظر بگیرید.
فرض کنید اطلاعاتی در مورد قیمت و سن 5 خودروی هم مدل جمعآوری کردهایم. اگر این اطلاعات را در قالب یک نمودار پراکنش نمایش دهیم شکل 3 حاصل میشود.
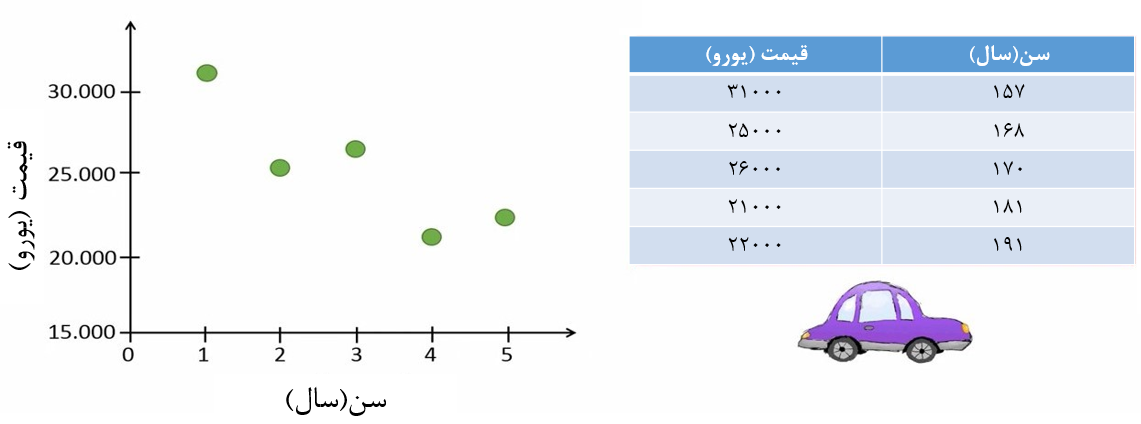
شکل 3. اطلاعات سن و قسمت 5 خودرو و نمودار پراکنش
حالا یک خط از میان نقاط عبور میدهیم تا شکل 4 بدست آید. همانطور که میبینید، در این مثال شیب خط رو به پائین است. پس رابطه منفی داریم. رابطه منفی یعنی وقتی یک متغیر افزایش مییابد، دیگری کاهش پیدا کند.
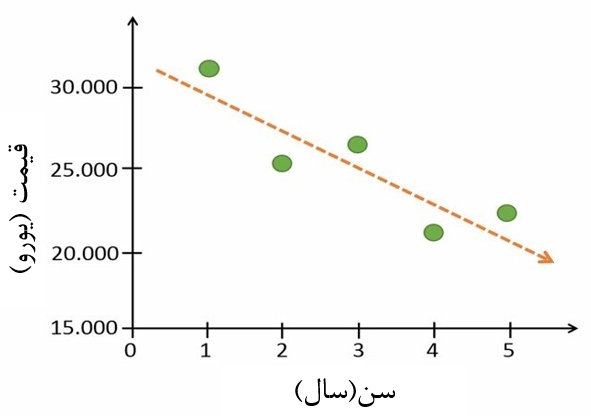
شکل 4. برازش خط از بین نقاط در اطلاعات سن و قیمت خودرو
بر خلاف رگرسیون، در همبستگی تفاوتی ندارد که چه متغیری روی محور Y قرار گیرد. پس ما نیازی به تعیین متغیر وابسته نداریم.
ضریب همبستگی پیرسون
یکی از کمیتهایی که برای بررسی رابطه بین دو متغیر استفاده میشود، ضریب همبستگی پیرسون است. این ضریب، ارتباط بین دو متغیر وابسته را اندازهگیری میکند و فرمول آن به شرح زیر است:
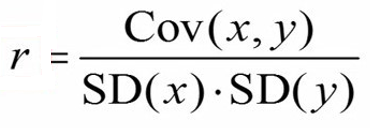
در صورت کسر، کوواریانس یا واریانس مشترک دو متغیر قرار دارد. در مخرج کسر، انحراف معیار دو متغیر در هم ضرب میشود.
اگر فرمول کوواریانس و انحراف معیارهای X و Y را در معادله جایگذاری کنیم، معادله ضریب همبستگی را به شکل زیر خواهیم داشت:
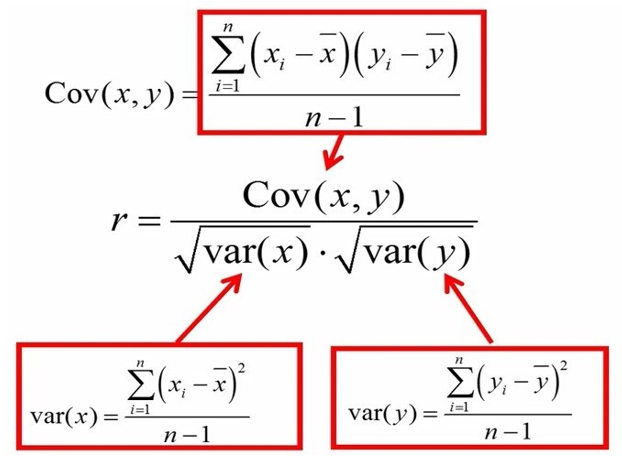
اگر دقت کنید، به راحتی میتوانیم عبارت n-1 را از صورت و مخرج کسر حذف کنیم. در این صورت معادله به شکل زیر در میآید.
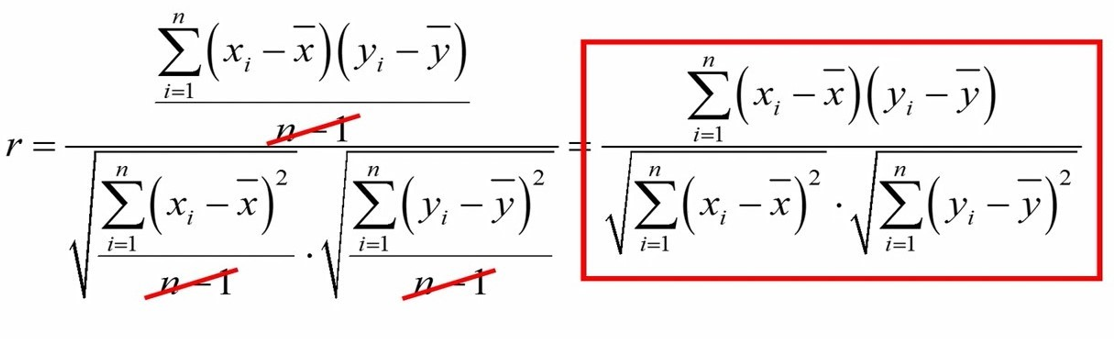
محاسبه رابطه بین دو متغیر
فرض کنید میخواهیم ارتباط بین دو متغیر در مثال قبل را با استفاده از ضریب همبستگی بدست بیاوریم.
به این منظور، ابتدا میانگینهای قد و وزن افراد را محاسبه میکنیم. میانگین وزن را 73 کیلوگرم و میانگین قد را 175.33 بدست آوردهایم. انحراف استانداردوزن را 10.16 و انحراف استاندارد قد را 12.56 محاسبه کردهایم. اطلاعات تحقیق را به شرح زیر مینویسیم:
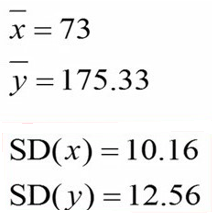
اگر با نحوه محاسبه میانگین و انحراف استاندارد آشنا نیستید مقالات مربوط به این مباحث را مطالعه کنید.
حالا نوبت محاسبه کوواریانس بین وزن و قد است. مقادیر را بصورت شکل زیر در فرمول کوواریانس قرار میدهیم و کوواریانس را محاسبه میکنیم.
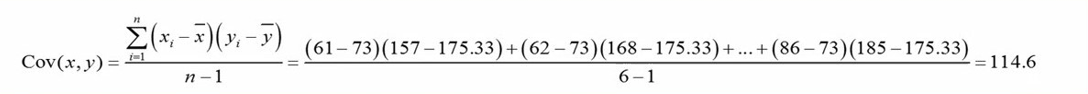
کوواریانس را برای این مثال 114.6 محاسبه کردهایم. کوواریانس یعنی چقدر تنوع مشترک دو متغیر چقدر است؟
مقدار کوواریانس را در فرمول قرار میدهیم و ضریب همبستگی را به شکل زیر محاسبه میکنیم:
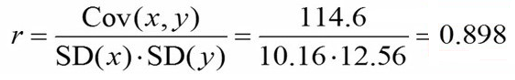
چون در این مثال ضریب همبستگی مثبت (0.898) است، دو متغیر رابطه هم سو دارند. به این معنی که با افزایش یکی، دیگری هم افزایش مییابد.
تفسیر ضریب همبستگی پیرسون
ضریب همبستگی پیرسون میتواند بین دو عدد 1- و 1+ باشد.
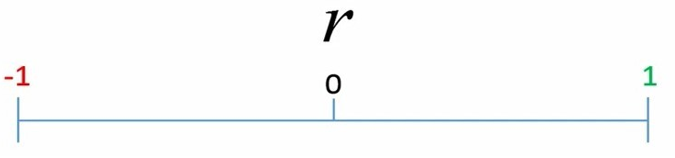
هر چه این ضریب به 1+ نزدیک تر باشد نشان دهنده ارتباط مثبت بالاتر و هر چه به 1- نزدیکتر باشد، نشان دهنده رابطه منفی بالاتر است. اگر این ضریب به صفر نزدیک باشد نشان میدهد که رابطه وجود ندارد.
ضریب همبستگی زمانی 1+ میشود که تمام نقاط دقیقاً روی خط با شیب مثبت واقع شده باشند. اگر تمام نقاط دقیقاً روی خط با شیب منفی واقع شوند، ضریب همبستگی 1- میشود. ضریب همبستگی زمانی صفر میشود که هیچ خطی را نتوان از بین نقاط عبور داد. در مقاله دوم آزمون فرضیات و پیشفرضهای همبستگی را با هم بررسی میکنیم.

نظرات :