قضیه حد مرکزی را به سادگی درک کنید: راهنمای تصویری گام به گام

مقدمه

آیا تا به حال به این فکر کرده‌اید که چرا نتایج بسیاری از آزمایش‌ها و نظرسنجی‌ها، حتی اگر به صورت تصادفی انتخاب شوند، اغلب به شکل یک منحنی زنگوله‌ای توزیع می‌شوند؟ از قد و وزن افراد گرفته تا نمرات آزمون‌ها و حتی توزیع خطاها در اندازه‌گیری‌ها، همه می‌توانند از این الگو پیروی کنند. این راز در مفهومی به نام “قضیه حد مرکزی” نهفته است.

تصور کنید که می‌خواهیم قد متوسط دانش‌آموزان یک مدرسه را تخمین بزنیم. اگر قد هر دانش‌آموز را یک متغیر تصادفی در نظر بگیریم، توزیع این متغیر می‌تواند هر شکلی داشته باشد. اما اگر به جای یک دانش‌آموز، قد متوسط یک نمونه بزرگ از دانش‌آموزان را در نظر بگیریم، چه اتفاقی می‌افتد؟ قضیه حد مرکزی به ما می‌گوید که با افزایش اندازه نمونه، توزیع میانگین‌های نمونه به تدریج به یک توزیع نرمال نزدیک می‌شود، حتی اگر توزیع اولیه متغیر تصادفی ما هر شکلی داشته باشد.

چرا دانستن قضیه حد مرکزی مهم است؟

• درک بهتر آمار و احتمال: این قضیه یکی از مهم‌ترین مفاهیم در آمار و احتمال است و به ما کمک می‌کند تا پدیده‌های تصادفی را بهتر درک کنیم.
• تحلیل داده‌ها: در بسیاری از تحلیل‌های آماری، از قضیه حد مرکزی برای استنباط درباره جمعیت استفاده می‌شود.
• تصمیم‌گیری در شرایط عدم قطعیت: این قضیه به ما کمک می‌کند تا در شرایطی که اطلاعات کامل نداریم، تصمیمات بهتری بگیریم.

در این مقاله، شما یاد خواهید گرفت:

• قضیه حد مرکزی چیست و چه معنایی دارد؟
• چرا توزیع نرمال اینقدر مهم است؟
• کاربردهای قضیه حد مرکزی در دنیای واقعی
• چگونه از این قضیه برای تحلیل داده‌های خود استفاده کنید؟

اگر به آمار و احتمال علاقه دارید و می‌خواهید درک عمیق‌تری از دنیای داده‌ها پیدا کنید، این مقاله برای شماست. با ما همراه باشید تا با استفاده از مثال‌های ساده و شبیه‌سازی‌های کامپیوتری، قضیه حد مرکزی را به طور کامل درک کنید.

به دلیل اینکه آزمون فرضیات پارامتریک عموماً بر مبنای فرض توزیع نرمال هستند، قضیه حد مرکزی یک مفهوم بسیار مهم و کلیدی برای آزمون فرضیات پارامتریک است.

مفهوم دقیق قضیه حد مرکزی

قضیه حد مرکزی به اینصورت تعریف می‌شود که توزیع میانگین نمونه‌های با حجم‌های بالا تقریباً نرمال است. اگرچه ممکن است توزیعی که ما از آن نمونه‌گیری می‌کنیم، نرمال نباشد.

مثلاً توزیع متغیر شکل 1 را در نظر بگیرید.

شکل 1. توزیع یک متغیر

مطابق شکل 1، توزیع این متغیر نرمال نیست و از سمت راست چولگی دارد.

فرض کنید از این توزیع 30 مشاهده به تصادف انتخاب می‌کنیم. میانگین این 30 مشاهده را محاسبه می‌کنیم. همین کار را 10000 بار انجام می‌دهیم. یعنی 10000 بار 30 تا مشاهده از توزیع انتخاب می‌کنیم و میانگین آن‌ها را حساب می‌کنیم. حالا 10000 میانگین داریم که این میانگین‌ها توزیع نرمال دارند (شکل 2).

شکل 2. توزیع متغیر اصلی و توزیع میانگین نمونه‌ها

پس ما یک توزیع داریم که مربوط به متغیراصلی است و یک توزیع هم داریم که مربوط به توزیع میانگین‌ مشاهده‌های گرفته‌ شده از توزیع اصلی است. اگر حجم نمونه‌ها بزرگتر از 30 باشد، توزیع میانگین‌ها تقریباً نرمال است. هر چند توزیع متغیر اصلی نرمال نباشد. این موضوع در شکل 2 نشان داده شده است.

مثال برای قضیه حد مرکزی

توزیع احتمالات یک تاس متقارن را در نظر بگیرید. توزیع احتمالات تاس یک توزیع ثابت است. یعنی اگر این تاس را بیندازیم، احتمال اینکه هر وجه تاس بیاید کاملاً مشابه است (شکل 1).

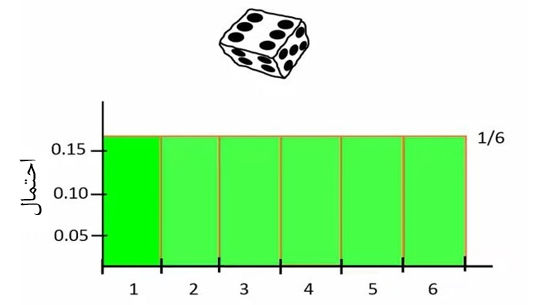
شکل 3. توزیع احتمالات وجه‌های مختلف یک تاس

در این تاس احتمال اینکه در یک پرتاب عدد 5 بیاید یک ششم است. یک ششم حدوداً 16.7 درصد می‌شود. این احتمال دقیقاً برابر با احتمال آمدن هر وجه دیگری از تاس می‌باشد.

فرض کنید یک تاس 5 بار ریخته می‌شود. در این 5 بار به ترتیب اعداد 2، 3، 4، 6 و 6 می‌آید. بنابراین، میانگین اعداد این 5 پرتاب برابر با 4.2 می‌شود.

حالا 5 بار دیگر تاس را پرتاب می‌کنیم. این بار میانگین 5 پرتاب ما 3.8 می‌شود. چون به تصادف این بار اعداد دیگری آمده است.

مجدداً 5 پرتاب دیگر انجام می‌دهیم. این بار میانگین 4.2 می‌شود. نهایتاً ما 6 مرتبه 5 پرتاب انجام می‌دهیم تا 5 میانگین بدست بیاوریم. این میانگین‌ها را در شکل 4 نشان داده‌ایم.

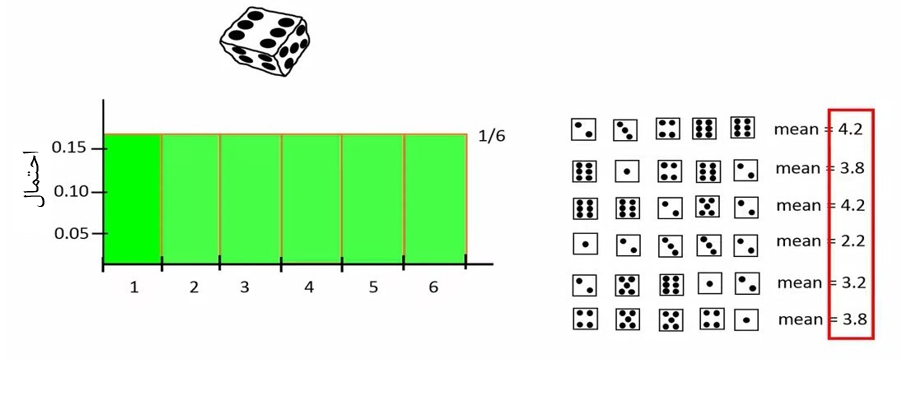
شکل 4. میانگین 6 مرتبه پرتاب 5 بار یک تاس

توزیع میانگین‌ها

به شکل 5 دقت کنید. الان ما 6 میانگین داریم که اگر دقت کنیم، می‌بینیم که این میانگین‌ها توزیع تقریباً نرمال دارند. می‌توانیم برای این میانگین‌ها هیستوگرام رسم کنیم (شکل5).

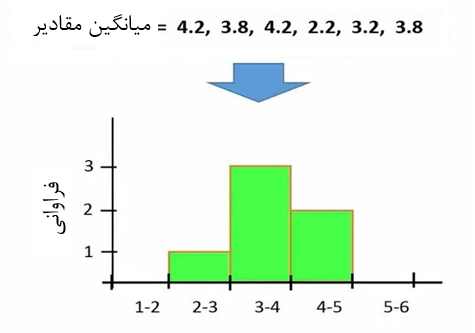
شکل 5. هیستوگرام میانگین‌ها

ارتفاع ستون اول سمت چپ در هیستوگرام نشان می‌دهد که بین میانگین‌ها یک عدد وجود دارد که در محدوده 3-2 است. ستون دوم نشان می‌دهد سه عدد وجود دارد که در محدوده 4-3 هستند. ستون سوم نیز نشان می‌دهد که دو عدد وجود دارد که در محدوده 5-4 هستند.

اگر منحنی توزیع نرمال را روی هیستوگرام قرار دهیم، می‌بینیم که توزیع این میانگین‌ها تقریباً نرمال است و میانگین مقادیر هم برابر با 3.5 می‌باشد (شکل 6).

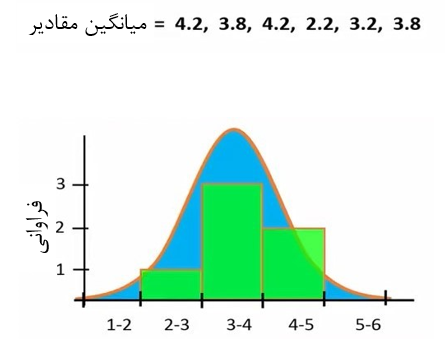
شکل 6. قرار دادن منحنی توزیع نرمال روی هیستوگرام

چرا میانگین مقادیر 3.5 می‌شود؟

چون ترکیبات عددی زیادی وجود دارد که اعدادی نزدیک به 3.5 به ما می‌دهد. در حالی‌که ترکیبات عددی کمی وجود دارد که میانگین‌های خیلی بالا یا پائین به ما بدهد.

به عنوان مثال احتمال بسیار کمی وجود دارد که میانگین 5 پرتاب اعدادی بالاتر از 5 یا 6 به ما بدهد.

بنابراین نتیجه می‌گیریم که اگرچه ما از یک جمعیت با توزیع کاملاً ثابت نمونه‌گیری انجام می‌دهیم، اما میانگین نمونه‌های ما توزیع نرمال دارند. این دقیقاً مفهوم قضیه حد مرکزی است.

نکاتی در مورد قضیه حد مرکزی

میانگین نمونه‌های اخذ شده از جمعیت همیشه توزیع نرمال ندارند. اینکه توزیع میانگین نمونه‌ها نرمال باشد بستگی به حجم نمونه و توزیع اولیه جمعیت دارد.

در این مثال، چون ما از یک جمعیت با توزیع ثابت متقارن نمونه گیری کرده‌ایم، حجم نمونه 5 برای هر نمونه کافی است تا توزیع میانگین نمونه‌های ما نرمال باشد.

حالا فرض کنید ما از یک جمعیت نامتقارن با توزیع نمایی نمونه‌گیری می‌کنیم. این جمعیت بر خلاف جمعیت دارای توزیع ثابت، انحراف زیادی از توزیع نرمال دارد و متقارن نیست (شکل 7).

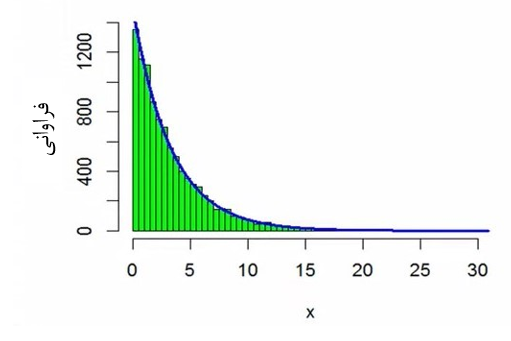
شکل 7. جمعیت با توزیع نمایی

اگر هر نمونه‌ای از این جمعیت می‌گیریم، 5 عضو داشته باشد و این کار را 10000 مرتبه تکرار کنیم. نهایتاً می‌توانیم هیستوگرام نرمال را رسم کنیم. می‌بینیم که توزیع میانگین نمونه‌ها هنوز چولگی دارد و به ظاهر مقداری از توزیع نرمال فاصله دارد (شکل 8).

شکل 8. توزیع میانگین نمونه‌ها با 5 عضو در هر نمونه

اما اگر حجم نمونه را به 30 افزایش دهیم، توزیع میانگین نمونه‌ها تقریباً نرمال خواهد بود (شکل 9).

شکل 9. توزیع میانگین نمونه‌ها با 30 عضو در هر نمونه

نکات مهم

قضیه حد مرکزی اینطور بیان می‌کند که میانگین نمونه‌های گرفته شده از جمعیت تقریباً دارای توزیع نرمال است، حتی اگر جمعیت اولیه توزیع نرمال نداشته باشد.

اگر حجم نمونه کم باشد و توزیع اولیه متغیر نرمال نباشد، توزیع میانگین نمونه ها نرمال نخواهد بود. هر چه حجم نمونه را افزایش دهیم، توزیع میانگین نمونه‌ها به توزیع نرمال نزدیکتر خواهد شد.

هر چه جمعیت اولیه ما از توزیع نرمال انحراف بیشتری داشته باشد، برای برقراری مفروض نرمالیتی، ما به حجم نمونه بیشتری نیاز داریم مثلاً اگر جمعیت اولیه ما توزیع نمایی داشته باشد نسبت به زمانی که توزیع جمعیت اولیه ثابت باشد، به حجم نمونه بیشتری برای برقراری مفروض نرمالیتی نیاز داریم.

برای اینکه بتوانیم فرض کنیم مقادیر میانگین نمونه‌ها دارای توزیع نرمال است، به عنوان یک قانون کلی می توانیم حجم نمونه 30 به بالارا در نظر بگیریم.