معادلات ساختاری در حالت نبود توزیع نرمال در آموس AMOS

در این مقاله تحلیل معادلات ساختاری را زمانی که داده‌ها از توزیع نرمال برخوردار نیستند بررسی می‌کنیم. توصیه می‌کنم قبل از مطالعه این بخش مقالات زیر را بخوانید:

• آشنایی با نرم افزار آموس (AMOS)
• تحلیل مسیر در آموس (AMOS)
• تحلیل عاملی تاییدی در آموس (AMOS)

برآورد حداکثر درستنمایی(MLE) روش برآورد استاندارد در اکثر برنامه های مربوط به معادلات ساختاری است. این رویکرد با این فرض انجام می‌شود که متغیرهای موجود در تحلیل، از توزیع نرمال چند متغیره تبعیت می‌کنند. چنانچه توزیع داده‌ها از توزیع نرمال چند متغیره تبعیت نکند یک یا چند مورد زیر رخ می‌دهد:

• مقادیر آزمون کای دو (Chi-square) متورم می شود. این موضوع می‌تواند  منجر به رد نادرست یک مدل مطلوب شود.
• این موضوع باعث می‌شود که خطاهای استاندارد کمتر از آنچه که بطور واقعی هستند برآورد شوند.  در نتیجه هنگام آزمایش پارامترهای مدل (به عنوان مثال، ضرایب مسیر، کوواریانس بین عوامل یا باقیمانده ها)  خطای نوع I بالا رفته  ضرایبی که در اصل غیر معنی‌دار هستند، معنی‌دار می‌شوند.

بررسی نرمال بودن داده‌ها در آموس

اگرچه نرمال بودن تک متغیره شرط لازم برای دستیابی به نرمال بودن چند متغیره است، اما این شرط کافی نیست. به عبارت دیگر، متغیرهای شما می توانند نرمال بودن تک متغیره را نشان دهند، اما ممکن است دارای توزیع نرمال چند متغیر نباشند. این نکته را هم به یاد داشته باشید که ارزیابی نرمال بودن تک متغیره و وجود مقادیر پرت تک متغیره می تواند در شناسایی متغیرها یا مواردی که ممکن است در غیر عادی بودن چند متغیره نقش داشته باشند مفید باشد.

در AMOS، اطلاعات مربوط به نرمال بودن تک متغیره (و چند متغیره) در مسیر Analysis Properties\Outputs موجود است (شکل بالا).

در منوی باز شده  روی قسمت  “Tests for normality and outliers” کلیک کنید.

نکته مهم: اگر در متغیرهای خود داده گم شده دارید، نمی توانید این اطلاعات را به دست آورید. این موضوع نشان می‌دهد که برای اینکه بتوانید این اطلاعات را به دست آورید، به یک مجموعه داده کامل (بدون مقادیر از دست رفته) نیاز دارید.

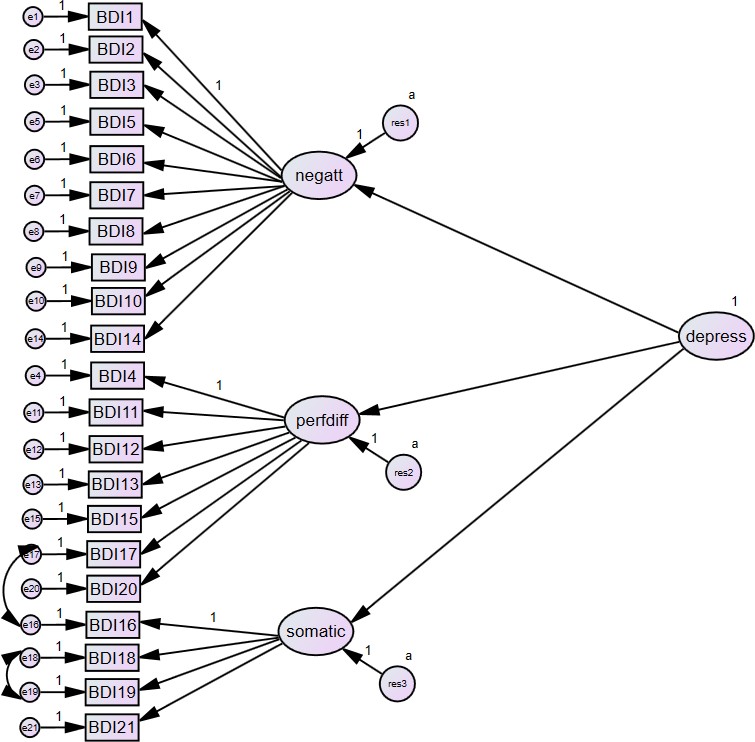
در شکل بالا یک تحلیل معادلات ساختاری از نوع تحلیل عاملی تاییدی را مشاهده می‌کنید (Byrne, 2010).

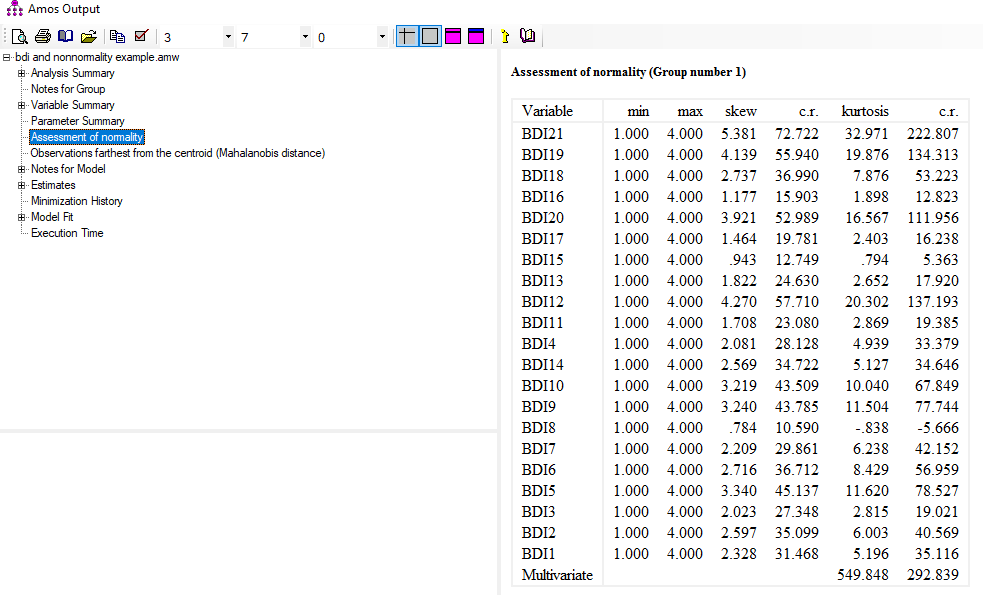
تحلیل خروجی نرم افزار آموس در ارتباط با نرمال بودن داده‌ها

خروجی مرتبط با تحلیل عاملی تاییدی (CFA) مرتبط با فصل 12 کتاب Byrne  در شکل بالا نشان داده شده است.
ستون‌های چولگی (skew) و کشیدگی (kurtosis) شامل مقادیر چولگی و کشیدگی تک متغیره است. ستون c.r حاوی نسبت های بحرانی برای آزمون هر یک از مقادیر است. نسبت های بحرانی (c.r) با در نظر گرفتن نسبت تخمین (برای چولگی یا کشیدگی) به خطای استاندارد آن تشکیل می‌شوند. این نسبت‌ها معادل مقادیر z-score هستند. با در نظر گرفتن آلفای 0.05، مقادیر Z کوچکتر از 1.96- و بزرگتر از 1.96+ نشان دهنده معنی‌داری آن آماره است.
به گفته کلاین (Kline, 2011) رد فرضیه صفر در ارتباط با وجود توزیع نرمال در داده‌ها هنگام استفاده از روش هایی که دارای نمونه بزرگ هستند (مانند معادلات ساختاری) آسان است. به عبارت دیگر زمانی که ما از نمونه‌های بزرگ استفاده می‌کنیم، یک انحراف بسیار کوچک از توزیع نرمال توسط آزمون‌های آماری معنی‌دار نشان داده می‌شود.  برای رفع این مشکل  ما از رویکرد توصیفی برای ارزیابی نرمال بودن داده‌ها استفاده می‌کنیم. در این زمینه قوانین سر انگشتی برای چولگی و کشیدگی وجود دارد که در ادامه آن‌ها را بررسی می‌کنیم.

قوانین سر انگشتی در مورد وجود توزیع نرمال در داده‌ها

وست و همکاران (West et al., 2005) قانون سرانگشتی برای مقدار کشیدگی به تصویب رسانده‌اند.  به این صورت که مقدار کشیدگی بیش از 7 (در مقدار مطلق) به عنوان  انحراف اساسی از نرمال بودن استفاده می‌شود.  همچنین مقادیر چولگی بیشتر از 3 (در مقدار مطلق) به عنوان نبود توزیع نرمال در داده‌ها در نظر گرفته می‌شود.
برن (به نقل از DeCarlo، 1997)خاطر نشان می‌کند که کشیدگی بیشتر از چولگی با معادلات ساختاری در ارتباط است. زیرا کشیدگی بر آزمون های واریانس و کوواریانس تأثیر می گذارد، در حالی که چولگی تأثیر بیشتری بر میانگین دارد. با استدلال او، به نظر می رسد که باید به مقوله کشیدگی توجه بیشتری کرد، در مقابل چولگی، هنگام ارزیابی اینکه آیا داده های فرد به طور قابل ملاحظه ای از حالت عادی فاصله می گیرند یا خیر استفاده می‌شود.

با استفاده از نسبت‌های بحرانی (c.r) و همچنین با بکارگیری قوانین سرانگشتی متغیرهای این تحقیق را بررسی می‌کنیم. نظر می‌رسد که همه متغیرها چه از نظر نسبت‌های بحرانی و چه از نظر قوانین سرانگشتی، چولگی و کشیدگی خیلی بالا نشان می‌دهند.

کشش چند متغیره (Multivariate) (ارائه شده در انتهای جدول بالا) برای ارزیابی اینکه آیا داده‌ها به طور معنی‌داری از نرمال بودن چند متغیره خارج می شوند استفاده می شود. نسبت بحرانی (c.r) و قوانین سرانگشتی قبلی را می توان برای پرداختن به این سوال به کار برد که آیا داده ها به طور معنی‌داری از نرمال بودن چند متغیره فاصله می گیرند یا خیر. با این وجود، Byrne (به نقل از بنتلر (2005))، پیشنهاد کرد که مقادیر کشیدگی چند متغیره > 5 را می توان به عنوان نشان دهنده خروج از نرمال بودن چند متغیره در نظر گرفت. با هر دو روش، کاملاً واضح است که متغیرهای این تحلیل منعکس کننده انحراف قابل توجهی از نرمال بودن چند متغیره هستند.

ارزیابی وجود مقادیر پرت چند متغیره (multivariate outliers)

اگرچه آموس AMOS اطلاعاتی در مورد مقادیر پرت تک متغیره نمی‌دهد، اما به ما این امکان را می‌دهد که حضور مقادیر پرت چند متغیره را در داده های خودمان بررسی کنیم. به این منظور برای هر واحد آزمایشی، یک مقدار مجذور فاصله ماهالونوبیس (Mahalanobis) ، به همراه آزمون آماری که می‌تواند در تشخیص موارد پرت چند متغیره به ما کمک کند، تولید می‌شود. فاصله ماهالونوبیس اندازه‌گیری فاصله مشاهده از مرکز (centroid) (به عنوان مثال، میانگین چند متغیره) برای متغیرهای موجود در تجزیه و تحلیل شما است. مشاهدات دارای مقادیر مجذور ماهالونوبیس به احتمال زیاد مقادیر پرت چند متغیره هستند. کلاین (Kline, 2011) یک مقدار p محافظه کارانه تری مانند p<0.001 را هنگام آزمون فرضیه آماری توصیه می کند. بایرن (Byrne, 2010) همچنین خاطرنشان می‌کند که مقدار مجذور فاصله ماهالونوبیس در یک داده پرت چند متغیره به طور قابل توجهی از سایر مقادیر  در مجموعه داده‌ها متفاوت است.

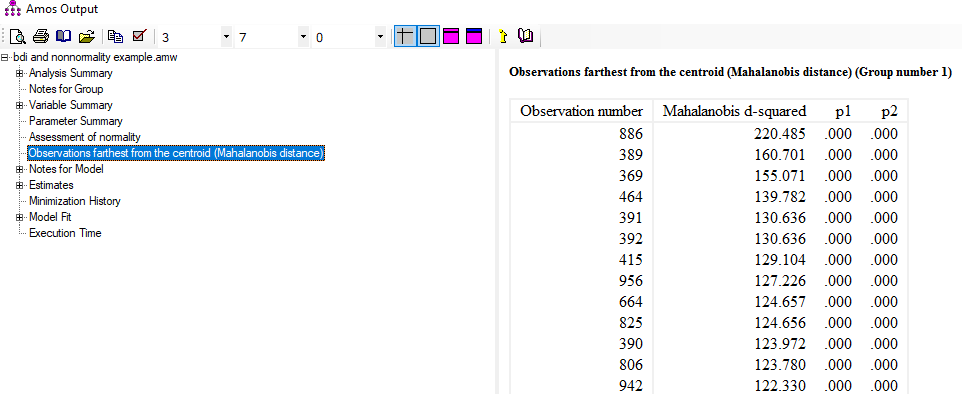
خروجی نرم افزار آموس در ارتباط با وجود مقادیر پرت چند متغیره

در شکل بالا مجموعه‌ای از مقادیر مجذور فواصل ماهالونوبیس همراه مقادیر p مرتبط وجود دارد (شکل بالا). آموس (AMOS) مقادیر فواصل ماهالونوبیس را به ترتیب رتبه نزولی ارائه می‌دهد.  بالاترین مقدار مجذور فاصله ماهالونوبیس 220.485 برای مشاهده 886 است. بزرگترین عدد در رتبه بعدی 160.701 است که مربوط به مشاهده 389 است. ستون p1 حاوی مقادیر p است که برای آزمایش اینکه آیا مشاهده مربوطه به طور معنی‌داری از مرکز داده‌ها فاصله می گیرد یا خیر استفاده می شود. با استفاده از معیار   (p<.001) که توسط کلاین ارائه شده است، می بینیم که همه نتایج آزمون ها معنی دار آماری هستند. با توجه به این نتیجه، واضح است که ما نمی‌توانیم از آزمون معناداری به عنوان استراتژی برای شناسایی نقاط پرت چند متغیره بالقوه در این مجموعه داده استفاده کنیم. مطابق معیار بایرن (Byrne, 2010)، یک “گسست” بالقوه در مقادیر فواصل ماهالونوبیس بین مشاهده 886 و 389 وجود دارد. در حالی که کاهش مقادیر فواصل ماهالونوبیس از مشاهده 389 به بعد بصورت تدریجی رخ می‌دهد. این نشان می دهد که مورد 886 می‌تواند یک مقدار پرت چند متغیره باشد.

ستون p2 حاوی مقادیر p است که برای آزمایش درستنمایی «مقادیر مرتب شده N به اندازه فاصله یا دورتر از مرکز» استفاده می شود. بایرن (Byrne, 2010) بیان می کند اگرچه اعداد کوچکی که در ستون اول (p1) ظاهر می شوند، قابل انتظار است، اعداد کوچک در ستون دوم (p2) با فرضیه نرمال بودن به احتمال زیاد از مرکز فاصله دارند.

اتخاد استراتژی‌های مختلف در صورت غیر نرمال بودن داده‌ها

در صورتی که داده‌ها غیر نرمال بودند می‌توانیم از استراتژی‌های زیر استفاده کنیم:

1. تشخیص و مدیریت موارد و/یا متغیرهایی که نرمال بودن تک متغیره را نشان نمی دهند.

2.  از روش تخمینی استفاده کنید که نرمال بودن چند متغیره را در نظر نگیرد، مانند تخمین ADF. (به طور کلی توصیه نمی شود، به جز نمونه هایی با 1000 تا 5000 مورد؛ Byrne، 2010)

3. از آزمون‌های تصحیح شده استفاده کنید. مانند آماره کای اسکوئر با مقیاس ساتورا-بنتلر (Satorra-Bentler). (متاسفانه این مورد از طریق آموس AMOS در دسترس نیست)

4. از روش بازنمونه‌گیری بوت استرپ استفاده کنید (در آموس AMOS در دسترس است).

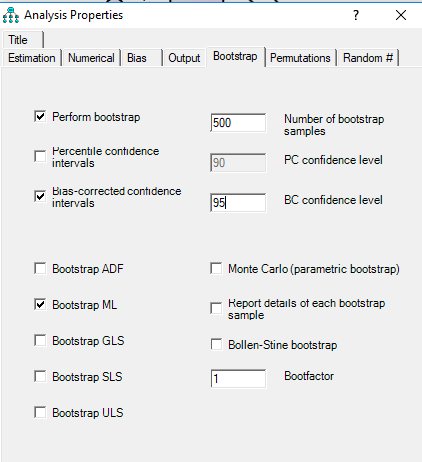
در قسمت Analysis properties بخش Bootstrap را انتخاب کنید و تیک موارد نشان داده شده در شکل بالا را فعال کنید.

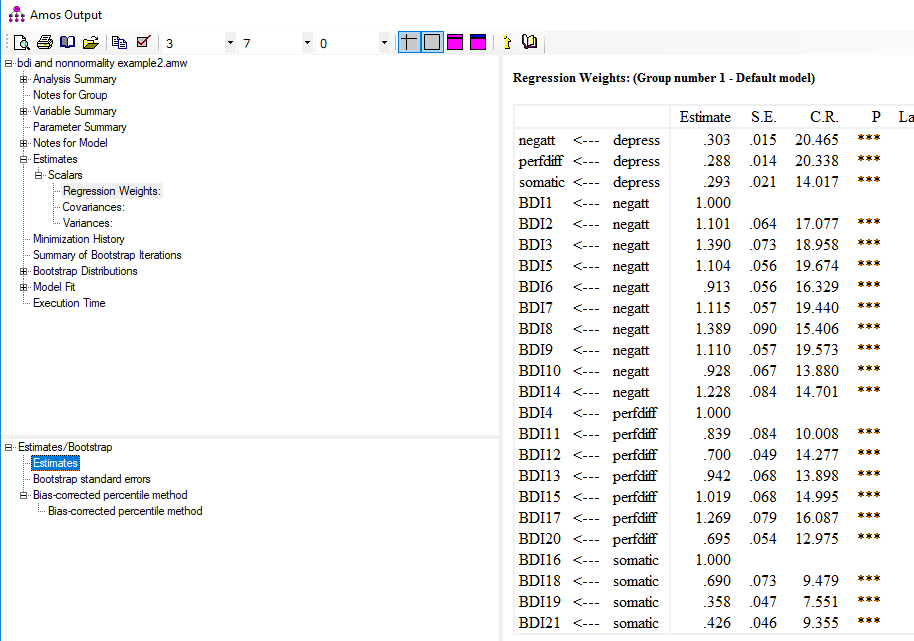
در قسمت Output، زمانی که تب Regression Weights فعال است، در قسمت Bootstrap گزینه Estimates را فعال کنید. در جدول بالا، SE خطای استاندارد بدست آمده از روش بوت استرپ را نشان می‌دهد. ستون برآوردها (Estimate) شامل بارهای عاملی غیراستاندارد (همانند جدول قبلی با برآوردهای ML) است. مقدار p-value از ظریق تقسیم آماره‌ها به خطای استاندارد حاصل می‌شود. خطاهای استاندارد در این روش از بوت استرپ بدست می‌آید.

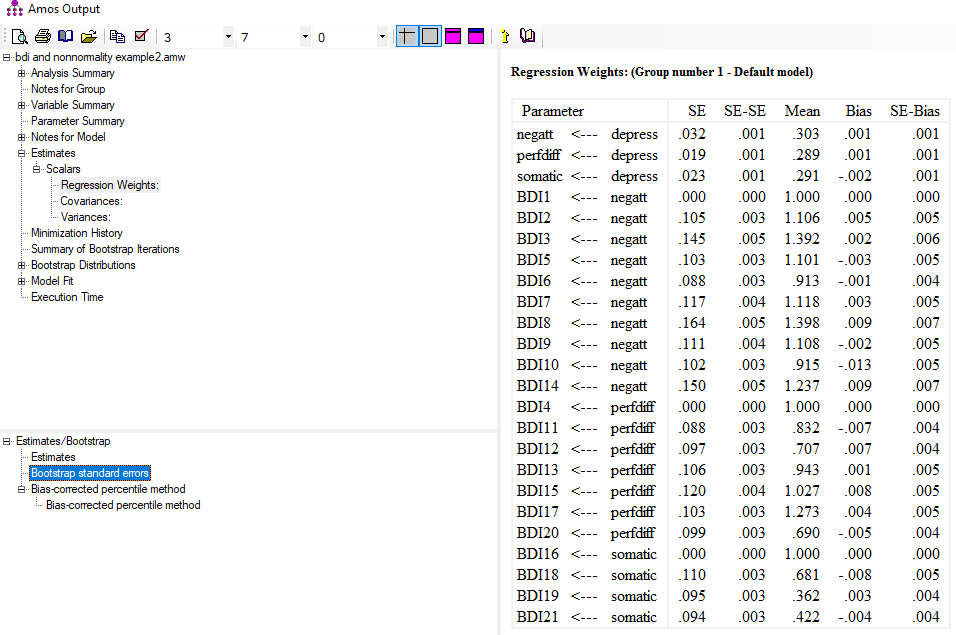
در بخش Bootstrap standard errors می‌توانید خطای استاندارد مربوط به هر کدام از خطاهای استاندارد و همچنین مقدار اریب (Bias) و خطای استاندارد اریب‌ها را نیز مشاهده کنید.

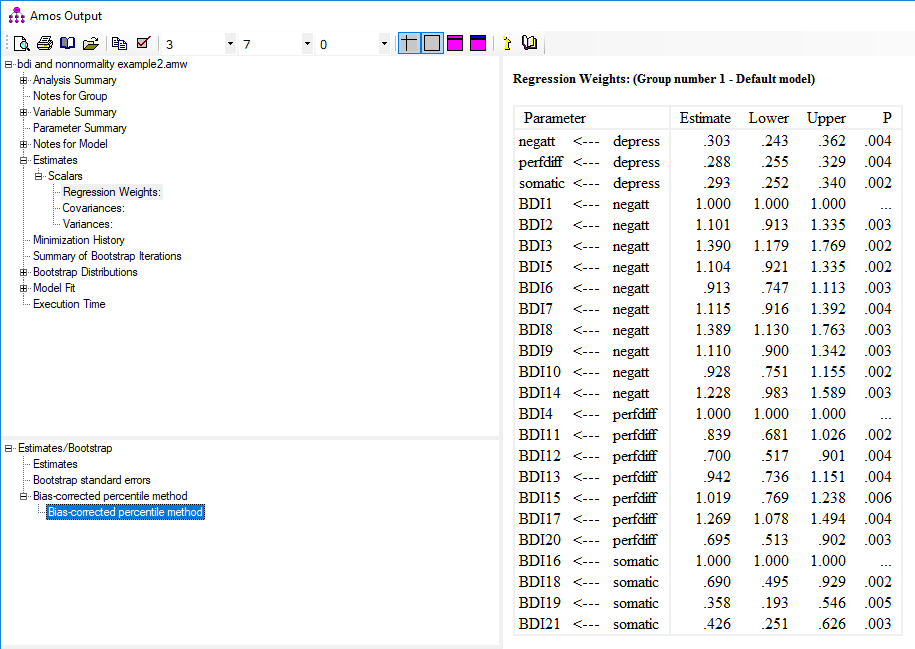
در بخش Bias-corrected percentile method می‌توانیم حدود اطمینان 95 درصد ضرایب و همچین مقدار P را مشاهده کنیم. چنانچه مقدار P کوچکتر از 0.05 باشد ضرایب را معنی‌دار تلقی می‌کنیم.

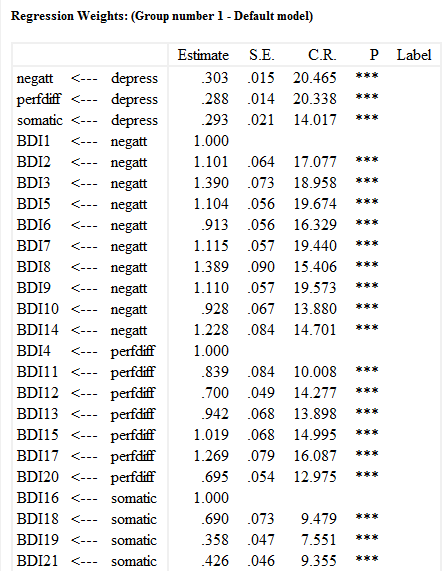
در شکل بالا  آزمون هر یک از ضرایب را بر مبنای روش حداکثر درستنمایی (ML) و بوت استرپ (Bootstrap) را در کنار هم مشاهده می‌کنید.

استفاده قبلی از bootstrapping فقط خطاهای استاندارد را برای پارامترهای  مدل تصحیح کرد. آنها هر گونه تأثیر سوگیری (Bias) را که غیر نرمال بودن چند متغیره ممکن است بر مقدار مجذور کای محاسبه شده  داشته باشد را تصحیح کردند.
همانطور که قبلاً اشاره کردیم، غیر نرمال بودن چند متغیره ممکن است منجر به تورم در مقدار آزمون کای اسکوئر شود که منجر به رد بی دلیل یک مدل خوب شود. یک رویکرد جایگزین برای آزمایش برازش مدل، استفاده از بالن-استاین بوت استرپ (Bollen-Stine bootstrap) به عنوان ابزاری برای ارزیابی برازش مدل است.
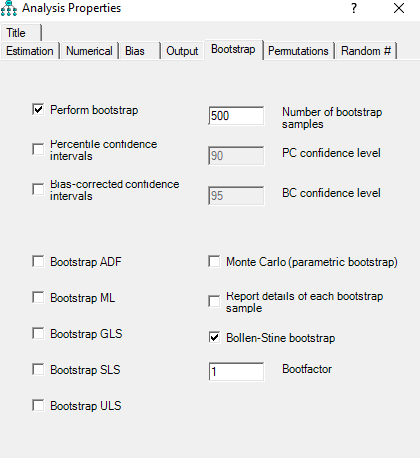
برای اجرای این بخش در قسمت Analysis properties در بخش Bootstrap، مطمئن شوید که روی Perform Bootstrap کلیک کرده اید و تعداد نمونه های بوت استرپ مورد نظر خود را مشخص کرده اید. سپس مانند شکل بالا روی Bollen-Stine bootstrap کلیک کنید.

نکته جانبی: وقتی Bollen-Stine bootstrap را انتخاب کرده اید، نمی توانید خطاهای استاندارد بوت استرپ و فواصل اطمینان را بدست آورید. پس فقط تیک Bootstrap و Bollen-stine bootstrap را فعال می‌کنیم.

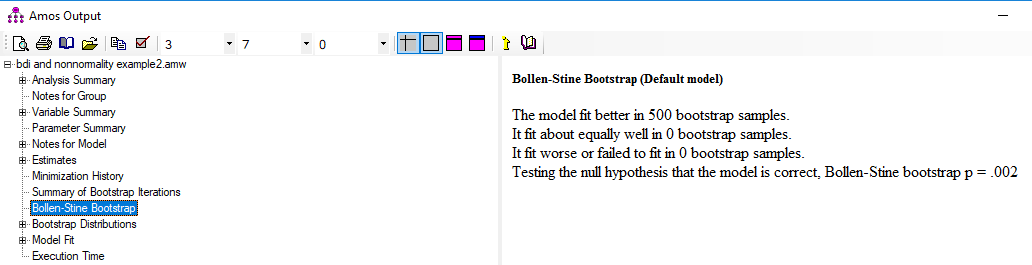
حالا در خروجی نرم افزار روی Bollen-Stine Bootstrap کلیک می‌کنیم. در این صورت می‌توانیم مقدار P تصحیح شده آزمون کای دو را ببینیم.

References

Byrne, B.M. (2010). Structural equation modeling with AMOS: Basic concepts, applications, and programming (2^nd ed). New York: Taylor & Francis.

Kline, R.B. (2011). Principles and practice of Structural Equation Modeling (3^rd ed). New York: The Guilford Press.