راهنمای جامع تحلیل عاملی مرتبه دوم در AMOS: از تئوری تا عمل

مقدمه

در بسیاری از مطالعات روان‌شناختی و علوم اجتماعی، محققان با سازه‌های پیچیده‌ای روبرو هستند که از چندین مؤلفه تشکیل شده‌اند. برای درک بهتر این سازه‌ها و روابط بین آن‌ها، تحلیل عاملی مرتبه دوم ابزاری قدرتمند است. این روش به ما اجازه می‌دهد تا ساختار درونی سازه‌ها را شناسایی کرده و روابط بین مؤلفه‌های سطح پایین و عوامل سطح بالا را بررسی کنیم. در این پژوهش، با استفاده از تحلیل عاملی مرتبه دوم در نرم‌افزار SPSS، مثالی را بطور کامل در این زمینه بررسی می‌کنیم. چنانچه آموزش من در مورد آشنایی مقدماتی با نرم افزار AMOS را قبلا ندیده‌اید لطفا ابتدا این آموزش را ببینید و با این نرم افزار آشنا شوید.

براون (2006) یک روش کلی برای انجام تحلیل عاملی مرتبه پیشنهاد می‌کند:

1. ساخت یک مدل تحلیل عاملی مرتبه اول مناسب:ابتدا باید یک مدل برای عوامل مرتبه اول بسازیم که از نظر آماری خوب باشد و از نظر تئوری نیز منطقی باشد. این مدل باید نشان دهد که چگونه متغیرهای مشاهده شده (مثلاً سوالات پرسشنامه) با عوامل پنهان (عوامل مرتبه اول) مرتبط هستند.

2. بررسی ارتباط بین عوامل مرتبه اول: بعد از ساخت مدل اول، باید بررسی کنیم که آیا عوامل مرتبه اول با هم ارتباط دارند یا خیر. اگر ارتباط بین عوامل اول قوی باشد، می‌توانیم فرض کنیم که یک یا چند عامل مرتبه دوم وجود دارد که این ارتباطات را ایجاد می‌کند.

3. آزمایش مدل تحلیل عاملی مرتبه دوم: در نهایت، مدل تحلیل عاملی مرتبه دوم را می‌سازیم و بررسی می‌کنیم که آیا این مدل به خوبی به داده‌ها برازش می‌کند یا خیر. این مدل نشان می‌دهد که چگونه عوامل مرتبه اول با عامل مرتبه دوم مرتبط است.

نکته: اگرچه می‌توان مدل‌هایی با عوامل مرتبه سوم و بالاتر را نیز ساخت، اما مدل‌های مرتبه دوم رایج‌تر هستند.

در ادامه سه مرحله‌ای را گفتیم را با مثال بررسی می‌‌کنیم:

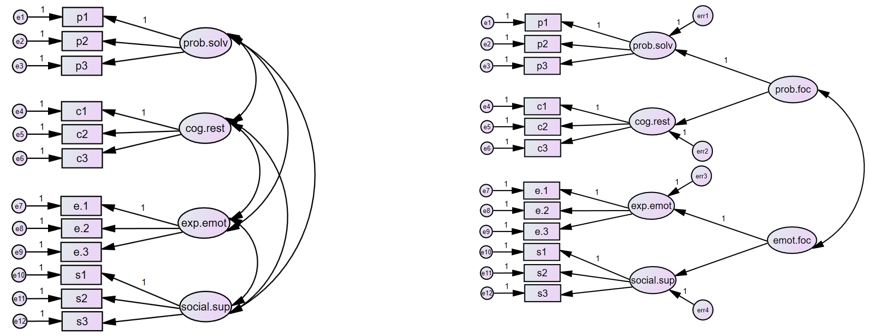
مدل تحلیل عاملی مرتبه دوم

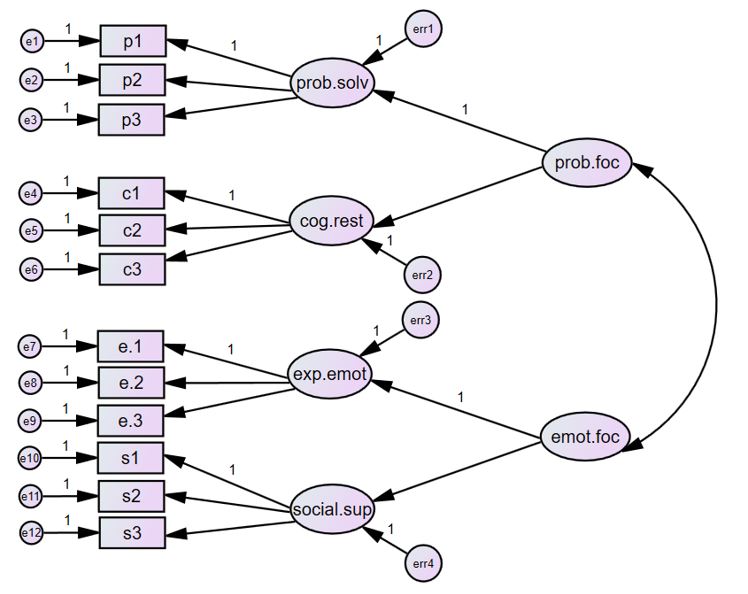
در شکل زیر، شما یک مدل تحلیل عاملی مرتبه دوم در نرم افزار AMOS می‌بینید که بر اساس مدل پیشنهادی در کتاب براون (2006، صفحه 322) ترسیم شده است. این مدل شامل چهار عامل مرتبه اول و دو عامل مرتبه دوم است که در آن، آیتم‌های پرسشنامه به عنوان شاخص‌های مشاهده‌ای در نظر گرفته شده‌اند.

• عوامل مرتبه اول: حل مسئله (prob.solv)، بازسازی شناختی (cog.rest)، ابراز احساسات (exp.emot) و حمایت اجتماعی (social.sup)
• عامل مرتبه دوم “مقابله متمرکز بر مسئله” (prob.foc) برای توضیح همبستگی بین عوامل مرتبه اول “حل مسئله” و “بازسازی شناختی” پیشنهاد شده است.
• عامل مرتبه دوم “مقابله متمرکز بر احساسات” (emot.foc) برای توضیح همبستگی بین عوامل مرتبه اول “ابراز احساسات” و “حمایت اجتماعی” پیشنهاد شده است.

این مدل نشان می‌دهد که چگونه عوامل مرتبه اول (مانند حل مسئله، بازسازی شناختی و …) با هم مرتبط هستند و چگونه این ارتباطات را می‌توان با عوامل مرتبه دوم (مانند مقابله متمرکز بر مسئله و مقابله متمرکز بر احساسات) توضیح داد.

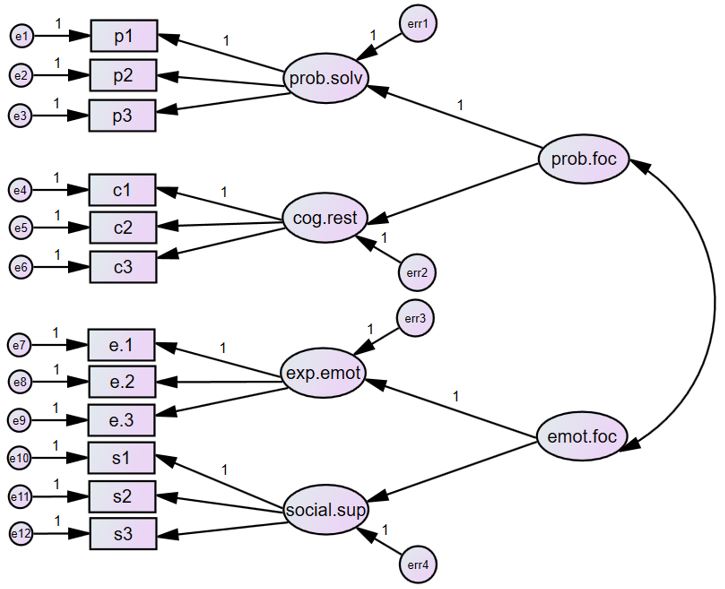
داده‌ها در نرم افزار SPSS

جدول ارائه شده یک ماتریس همبستگی است که در نرم‌افزار آماری SPSS وارد شده است. این ماتریس، روابط بین متغیرهای مختلف را نشان می‌دهد.

ستون‌های جدول:

• rowtype: نوع داده را مشخص می‌کند. در اینجا، تا ردیف 12 مربوط به همبستگی (corr)، ردیف 13 انحراف معیار (stddev) و ردیف 14 تعداد داده‌ها را نشان می‌دهد.
• varname: نام متغیر را نشان می‌دهد. در این مثال، متغیرها با حروف p (برای حل مسئله)، c (برای محدودیت شناختی)، e (برای ابراز احساسات) و s (برای حمایت اجتماعی) و اعداد نشان داده شده‌اند.
• اعداد: ضرایب همبستگی بین متغیرها را نشان می‌دهند. به عنوان مثال، همبستگی بین متغیر p1 و p2 برابر با 0.780 است. دو ردیف آخر نیز به ترتیب مربوط به انحراف معیار متغیرها و تعداد داده‌ها می‌باشد.

انجام تحلیل عاملی مرتبه دوم

در ادامه سه مرحله‌ تحلیل عاملی مرتبه دوم را در نرم افزار AMOS انجام می‌دهیم.

مراحل 1 و 2: مشخص کردن و آزمون مدل عاملی مرتبه اول، و ارزیابی همبستگی‌ها بین عامل‌ها.

مطابق با شکل زیر گزینه “Standardized estimates” را از منو “Analysis Properties” فعال کنید.

هنگامی که روی “Standardized estimates” کلیک می‌کنید، نه تنها ضرایب بارگذاری استاندارد شده برای همه آیتم‌ها را دریافت می‌کنید، بلکه همبستگی‌ها بین عوامل پنهان را نیز مشاهده می‌‌کنید.

نکته جانبی: از آنجایی که هر آیتم فقط روی یک عامل بارگذاری می‌شود (یعنی بارگذاری‌های متقاطع وجود ندارد)، بارهای عاملی نشان‌دهنده همبستگی بین هر آیتم و عامل مربوط به آن است.

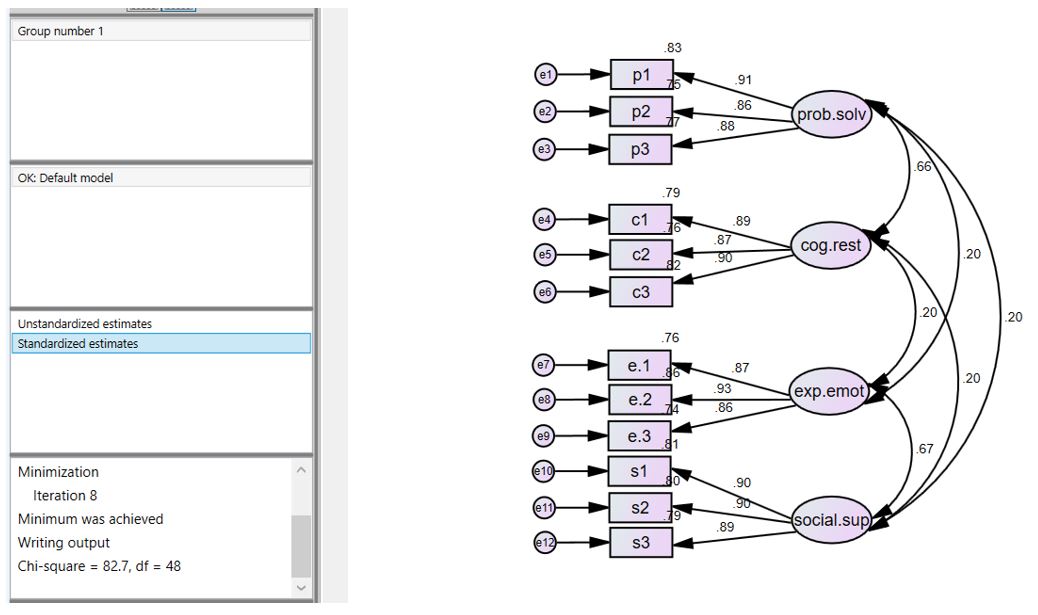
تفسیر ضرایب تحلیل عاملی

بر اساس شکل زیر بارهای عاملی نشان می‌دهند که روابط قوی بین عوامل مرتبه اول و شاخص‌های آن‌ها وجود دارد. همبستگی بین عوامل حل مسئله (porb.solv) و محدودیت شناختی (cog.rest) قوی است (r=.66)، همچنین همبستگی بین عوامل ابراز احساسات (exp.emot) و حمایت اجتماعی (social.sub) نیز قوی است (r=.67). نکته قابل توجه این است که عوامل حل مسئله و محدودیت شناختی بسیار کم با دو عامل دیگر همبستگی دارند.

الگوی همبستگی‌ها نشان می‌دهد که ممکن است یک عامل مرتبه دوم بتواند همبستگی بین عوامل حل مسئله (porb.solv) و محدودیت شناختی (cog.rest) را توضیح دهد، در حالی که یک عامل مرتبه دوم دیگر ممکن است بتواند همبستگی بین ابراز احساسات (exp.emot) و حمایت اجتماعی (social.sub) را توضیح دهد.

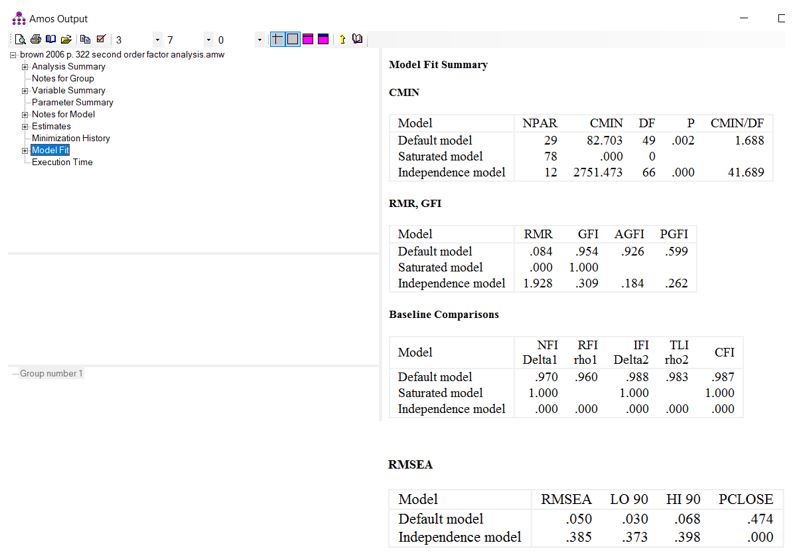
چون هدف ما تحلیل عاملی مرتبه دوم است از بررسی خروجی هایی که تخمین‌های استاندارد و غیر استاندارد را نشان می‌دهد صرف نظر می‌کنیم و فقط قسمت “Model fit” یا برازش مدل را بررسی می‌کنیم.

تفسیر شاخص‌های برازش مدل در خروجی نرم افزار AMOS

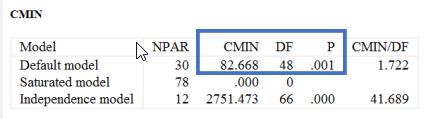
آزمون مربع کای

مطابق با شکل زیر عبارت CMIN که در خروجی ظاهر می‌شود، در واقع مقدار مربع خی است که روشی عمومی برای آزمون برازش مدل است. آزمون برازش مربع خی برای ارزیابی اینکه آیا یک مدل به طور معنی‌داری  از یک مدل کاملاً برازش شده فاصله دارد یا خیر، استفاده می‌شود (کلاین، 2016).

• DF (درجه آزادی): تعداد پارامترهای آزاد در مدل است.
• P-value (مقدار احتمال): سطح معنی‌داری است.
• تصمیم‌گیری: عموماً، اگر P-value کمتر یا مساوی 0.05 باشد، فرضیه صفر (مدل برازش کامل) رد می‌شود.

در داده‌های ما، آزمون برازش مربع خی معنی‌دار است (χ²(48)=82.668, p=.001). بنابراین، ما فرضیه برازش کامل را رد می‌کنیم.

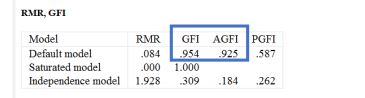
آزمون نکویی برازش مدل

مطابق با شکل زیر، شاخص‌های برازش مطلق مانند GFI و AGFI نشان می‌دهند که مدل ما تا چه اندازه می‌تواند داده‌ها را بازتولید کند (ویتاکر، 2016). به طور معمول، مقادیر GFI/AGFI برابر یا بیشتر از 0.90 نشان‌دهنده برازش قابل قبول مدل است (ویتاکر، 2016). توجه داشته باشید که در نرم‌افزار AMOS، زمانی که داده‌های گم شده وجود داشته باشد، GFI و AGFI محاسبه نمی‌شوند. مقادیر GFI و AGFI برای مدل چهار عاملی فعلی ما هر دو نشان می‌دهند که مدل به خوبی به داده‌ها برازش می‌کند.

شاخص‌های برازش مقایسه‌ای

کمیت‌های TLI و CFI شاخص‌های برازش افزایشی هستند که می‌توانند برای ارزیابی برازش یک مدل در مقایسه با یک مدل کاملا مستقل استفاده شوند. این شاخص‌ها معمولاً بین 0 و 1 قرار دارند (اگرچه ممکن است گاهی مقادیر کمی بالاتر از 1 هم داشته باشند). مقادیر ≥ 0.90 برای این شاخص‌ها نشان‌دهنده برازش قابل قبول مدل تلقی می‌شود (ویتاکر، 2016)، اما مقادیر ≥ 0.95  به عنوان شواهدی از برازش برتر در نظر گرفته شوند (بیرن، 2010، صفحه 79). برای مدل فعلی، هم TLI و هم CFI نشان می‌دهند که مدل چهار عاملی فعلی برازش بسیار خوبی با داده‌ها دارد.

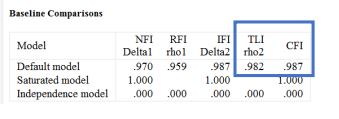
شاخص RMSEA

کمیت RMSEA (Root Mean Square Error of Approximation) یا ریشه دوم میانگین مربعات خطای تقریب یک شاخص برازش مطلق است که نشان می‌دهد مدل چقدر بر داده‌ها برازش می‌کند (کلاین، 2016).

• مقدار 0: بهترین برازش را نشان می‌دهد.
• مقادیر بالاتر از 0: نشان‌دهنده برازش بدتر است.

مقادیر RMSEA کمتر یا مساوی 0.05 معمولاً نشان‌دهنده یک مدل با برازش نزدیک است. مقادیر بین 0.08 و 0.10  یا حتی تا 0.10  قابل قبول در نظر گرفته می‌شوند. کلاین (2016) پیشنهاد می‌کند که RMSEA برابر یا بزرگتر از 0.10 نشان‌دهنده مشکلات جدی‌تر در مشخصات مدل است.

در خروجی ما، RMSEA برابر با 0.051 است که بین 0.05 (برازش نزدیک) و 0.10 (برازش ضعیف) قرار دارد. بنابراین، RMSEA بر اساس مدل ما نشان می‌دهد که مدل به خوبی به داده‌ها برازش نمی‌کند، اما با این حال، برازش قابل قبولی دارد.

آزمون PCLOSE روش دیگری برای ارزیابی برازش یک مدل بر اساس RMSEA است. اگر فرض کنیم RMSEA ≤ 0.05 باشد نشان‌دهنده یک مدل با برازش نزدیک است، آنگاه نتیجه PCLOSE > 0.05 می‌تواند به عنوان پشتیبانی از فرضیه صفر در رابطه با برازش نزدیک مدل در نظر گرفته شود (کلاین، 2016).

در تحلیل فعلی ما، PCLOSE برابر با 0.431 است که نشان می‌دهد برآورد نقطه‌ای RMSEA برابر با 0.051 به طور معنی‌داری  با آنچه ممکن است از یک مدل با برازش نزدیک انتظار داشته باشیم، متفاوت نیست (معیار 0.05 یا کمتر).

فاصله اطمینان 90% برای RMSEA نیز از 0.032 (حد پایین) تا 0.070 (حد بالا) متغیر است. حد پایین با معیار برازش نزدیک سازگار است، در حالی که حد بالا با معیار برازش قابل قبول سازگار است. این نتیجه همچنین نشان می‌دهد که مدل ما برازش قابل قبول، اگرچه نه نزدیک، به داده‌ها دارد.

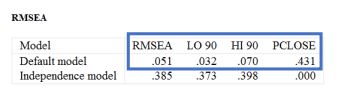
شاخص SRMR

شاخص SRMR (Standardized Root Mean Square Residual) نیز یک شاخص برازش مطلق رایج است که توسط کلاین (2016)  توصیه شده  است. کلاین (2016) SRMR را به عنوان “اندازه‌گیری میانگین مطلق باقیمانده همبستگی” توصیف می‌کند که نشان‌دهنده “تفاوت کلی بین همبستگی‌های مشاهده شده و پیش‌بینی شده” است. ویتاکر (2016)، برای کمیت SRMR، دستورالعمل‌های زیر را ارائه می‌دهد:

• مقادیر SRMR تا 0.05 نشان‌دهنده یک مدل با برازش خوب است.
• مقادیر SRMR تا 0.10 نشان‌دهنده برازش قابل قبول است.
• مقادیر SRMR بزرگتر از 0.10 نشان‌دهنده برازش ضعیف است.

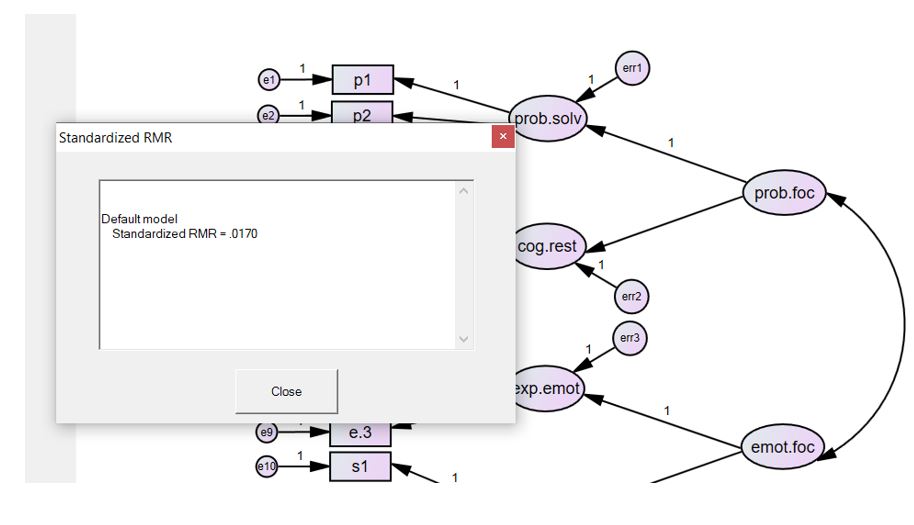
متأسفانه، نرم افزار AMOS به طور خودکار SRMR را همراه با سایر شاخص‌های برازش محاسبه نمی‌کند. برای محاسبه SRMR، می‌توانید به مسیر زیر در AMOS بروید:

مطابق با شکل زیر از منوی Plugins (افزونه‌ها) قسمت Standardized RMR (SRMR استاندارد شده) را انتخاب کنید. هنگامی که روی این گزینه کلیک می‌کنید، یک کادر خالی باز می‌شود. کافی است تحلیل را با باز بودن این کادر اجرا کنید تا SRMR ظاهر شود. پس از اتمام، روی “Close” کلیک کنید.

توجه: اگر داده گم شده در بین داده‌های شما باشد، نمی‌توانید SRMR را در AMOS محاسبه کنید. در مثال ما، SRMR برابر با 0.0170 است که نشان‌دهنده برازش خوب مدل شما است.

مرحله سوم :آزمون مدل با عوامل سطح بالاتر

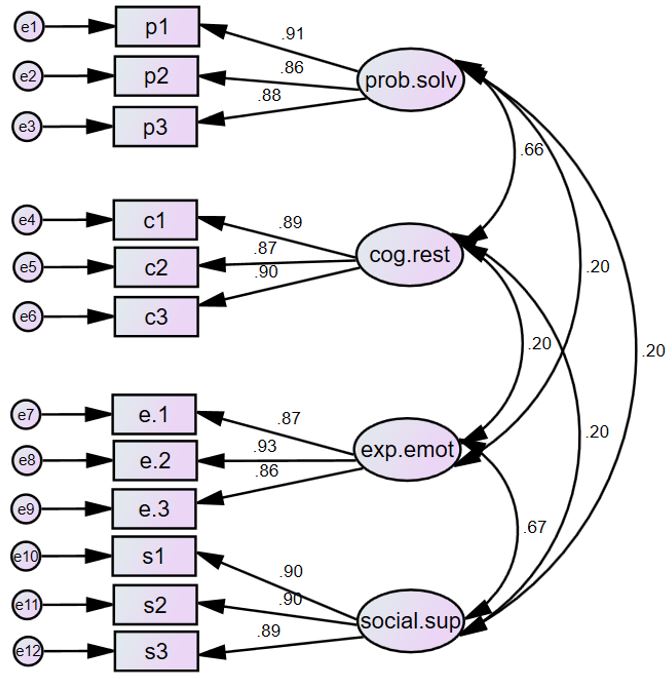
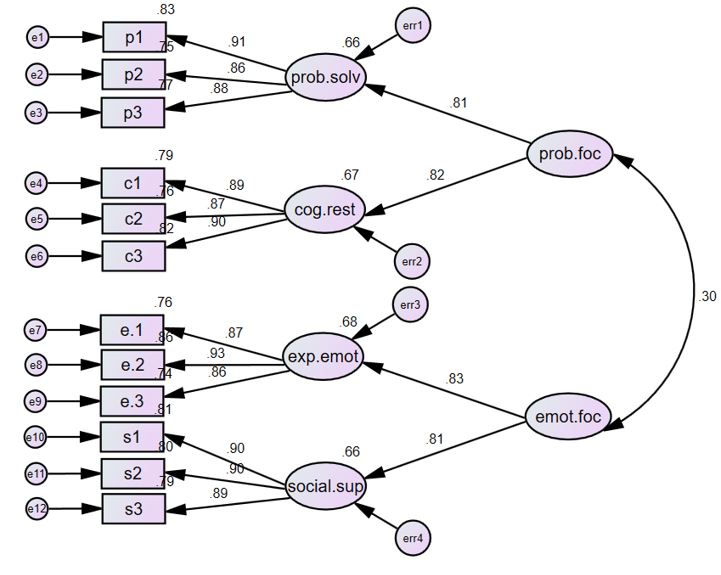
اکنون، مدل پیشنهادی اصلی را با دو عامل مرتبه دوم آزمایش می‌کنیم: “مقابله متمرکز بر مسئله” و “مقابله متمرکز بر احساسات” (براون، 2006).

همانطور که در شکل زیر مشاهده می‌کنید، ما همبستگی‌ها بین عوامل مرتبه اول را حذف کرده‌ایم و فلش‌هایی از عوامل مرتبه دوم به عوامل مرتبه اول کشیده‌ایم. این بر اساس فرض ما است که عوامل مرتبه دوم همبستگی‌های بین عوامل مرتبه اول را توضیح می‌دهند.

همچنین توجه داشته باشید که هر عامل مرتبه اول دارای یک نشانگر خطا است. ما همچنین یک همبستگی بین دو عامل مرتبه دوم قرار داده‌ایم.

چند نکته دیگر:

1. در مدل تحلیل عاملی مرتبه اول، می‌توانستیم واریانس عوامل نهفته را برابر با 1 ثابت کنیم، به جای ثابت کردن یک ضریب مسیر از هر عامل به شاخص‌های آن. هر دو رویکرد می‌توانستند برای شناسایی استفاده شوند. هر دو مشخصات مدل منجر به برازش یکسان می‌شوند و راه‌حل کاملاً استاندارد شده با هر دو مشخصات یکسان خواهد بود.

2. با این حال، در این مدل، نمی‌توانید واریانس عوامل مرتبه اول را برابر با 1 ثابت کنید، زیرا این عوامل اکنون دارای نشانگر خطا هستند که با آن‌ها مرتبط هستند. بنابراین، تنها گزینه شما برای شناسایی در سطح اول، ثابت کردن یک ضریب مسیر از عوامل به یک متغیر مرجع برابر با 1 است.

3. در شکل زیر می‌بینید که من یک مسیر از هر عامل مرتبه دوم به یک عامل مرتبه اول را برابر با 1 ثابت کرده‌ام. این کار برای دستیابی به شناسایی در سطح دوم انجام شده است. با این حال، می‌توانستم به جای آن، واریانس عوامل مرتبه دوم را برابر با 1 ثابت کنم. هر دو مشخصات مدل منجر به برازش یکسان می‌شوند، و راه‌حل کاملاً استاندارد شده با هر دو مشخصات یکسان خواهد بود.

در شکل زیر ضرایب استاندارد شده برای مدل فعلی نشان داده شده‌اند. بارهای عاملی استاندارد عوامل مرتبه دوم مانند عوامل مرتبه اول  تفسیر می‌شوند. همانطور که می‌بینید، بارهای عاملی استاندارد مرتبط با عوامل مرتبه دوم همگی مقادیر بالایی هستند. همچنین همبستگی مثبت متوسط (r=.30) نیز بین دو عامل مرتبه دوم وجود دارد.

خروجی‌های نرم افزار در رابطه با تحلیل عاملی مرتبه دوم در ادامه آورده شده است.

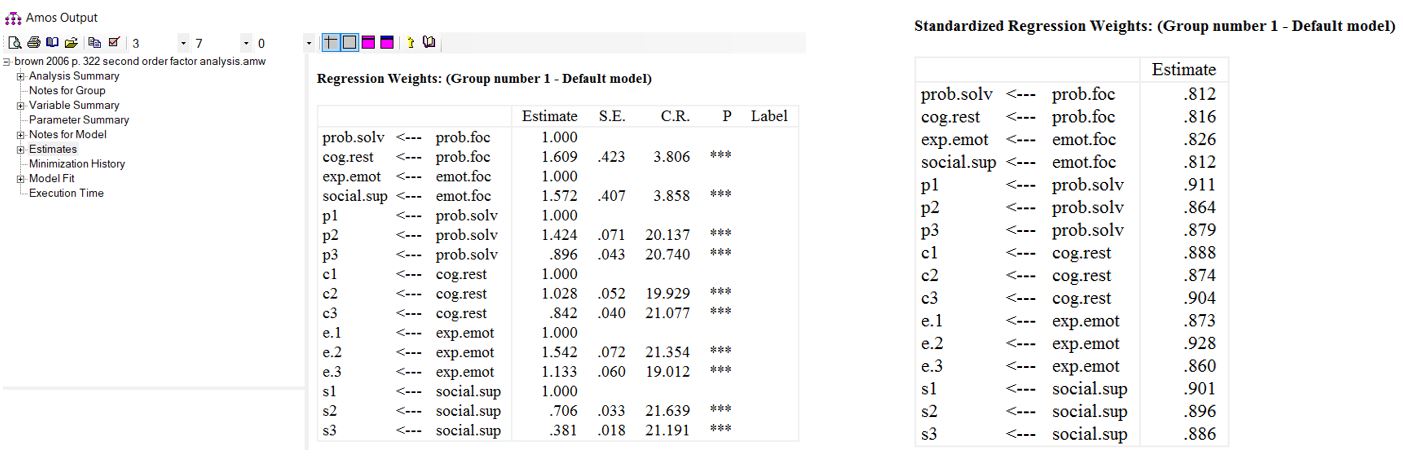
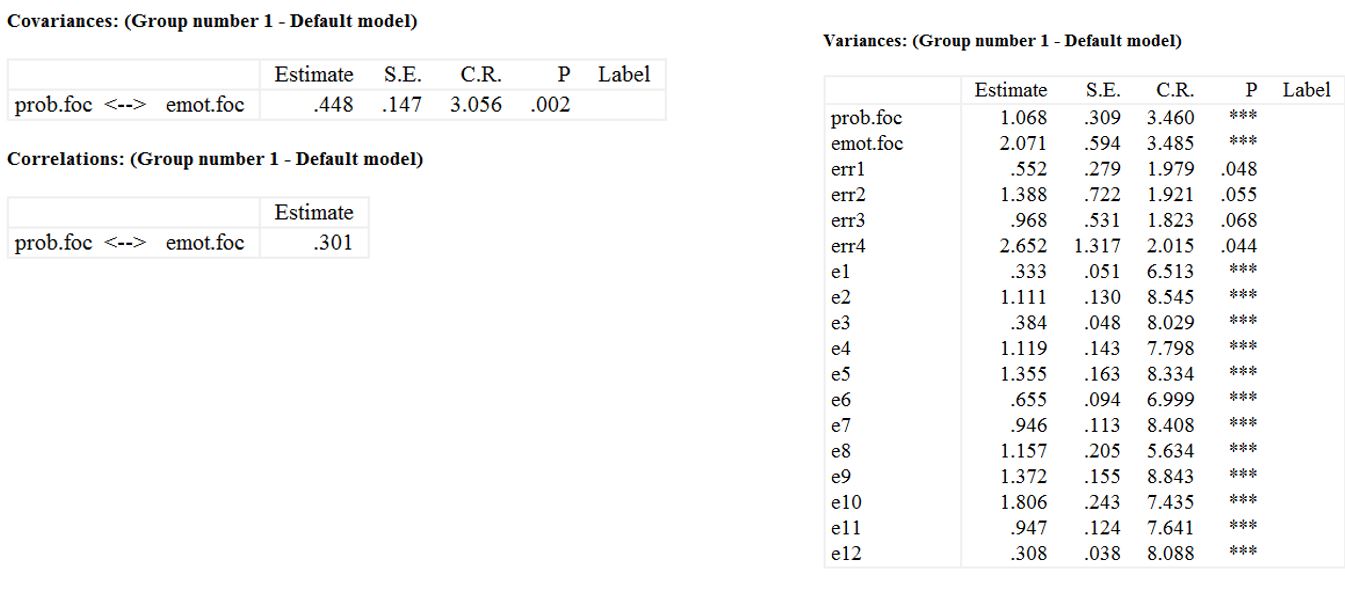
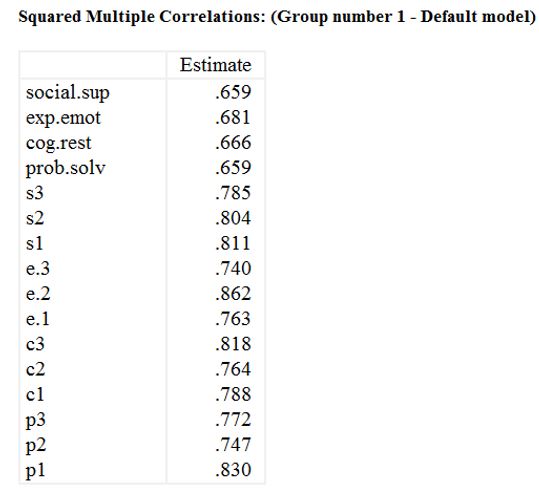
اگرچه فرضیه برازش دقیق بر اساس آزمون مربع خی رد شده است (χ²(49)=82.703، p=.002)، اما شاخص‌های GFI (0.954)، AGFI (0.926)، TLI (0.983)، CFI (0.987)، RMSEA (0.05) و PCLOSE (0.474) همگی نشان‌دهنده برازش خوب مدل هستند.

علاوه بر این، شاخص SRMR (0.0170) نشان می‌دهد که ما یک مدل با برازش خوب داریم (شکل زیر).

می‌توانیم با استفاده از آزمون تفاوت مربع خی، بررسی کنیم که آیا انجام یک مدل عامل مرتبه دوم منجر به کاهش معنی‌دار در برازش نسبت به مدل مرتبه اول می‌شود یا خیر، به شرطی که مدل مرتبه اول در مدل مرتبه دوم تو در تو باشد (براون، 2006).

مطابق با شکل زیر مقدار مربع خی برای مدل اول فقط کمی کوچکتر از مدل دوم است. درجه آزادی برای مدل اول کوچکتر از مدل دوم است زیرا یک پارامتر کمتر در مدل دوم برآورد می‌شود.

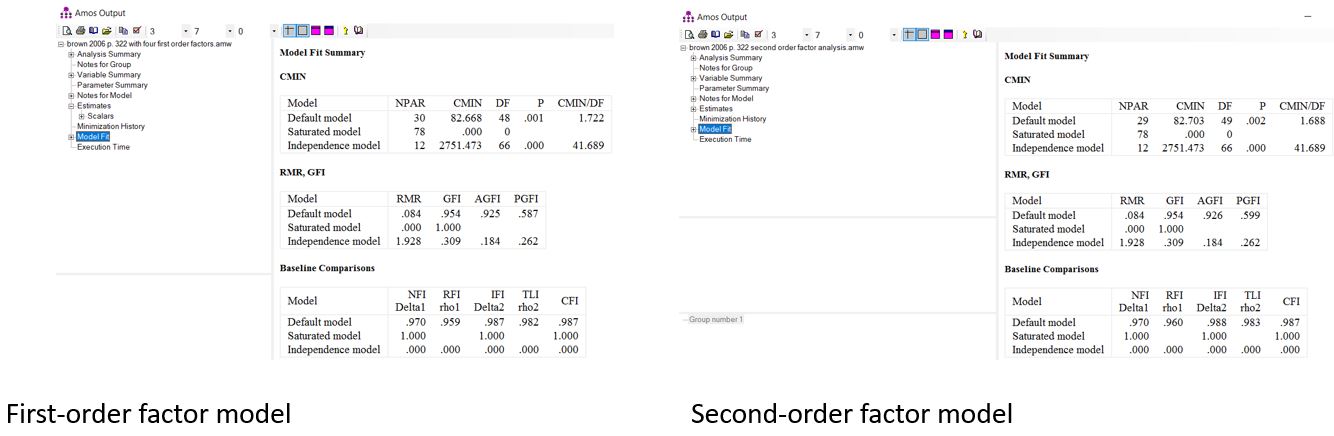
ما مقدار آزمون مربع خی و درجه آزادی برای آزمون تفاوت مربع خی را به روش زیر محاسبه می‌کنیم:

در مرحله بعد، مقدار محاسبه شده تفاوت مربع خی را با مقدار جدول مربع خی (که می‌توان آن را در بسیاری از کتاب‌های آمار یا آنلاین یافت) مقایسه می‌کنیم تا تعیین کنیم آیا کاهش معنی‌دار در برازش از مدل اول (عوامل مرتبه اول) به مدل دوم (عوامل مرتبه دوم) وجود دارد یا خیر. مقدار بحرانی جدول مربع خی برای 1 درجه آزادی و با فرض α=0.05 برابر با 1.84 است. از آنجایی که مقدار محاسبه شده مربع خی ما (0.035) کمتر از 1.84 است، ما فرضیه صفر را حفظ می‌کنیم که مدل عامل مرتبه دوم به طور معنی‌داری بدتر از مدل مرتبه اول برازش نمی‌شود (زیرا p>0.05). این یافته از مدل عامل مرتبه دوم پشتیبانی می‌کند.