رگرسیون خطی (قسمت دوم: حداقل مربعات)
در این مقاله روش حداقل مربعات برای برازش خط رگرسیون را توضیح میدهیم. این مقاله ادامه قسمت اول مبحث رگرسیون خطی است.
مثال رگرسیون خطی
در قسمت اول از رگرسیون خطی دیدیم که چطور به سادگی میتوانیم از رگرسیون خطی استفاده کنیم و با استفاده سن خودرو قیمت آن را تخمین بزنیم.
معادله خط رگرسیون برای تخمین قیمت خودرو را به شرح زیر بدست آوردیم:

همانطور که ملاحظه میکنید، عرض از مبدأ معادله 30.57 است. به این معنی که خط رگرسیون محور قیمت را در نقطه 30.57 قطع میکند. شیب خط هم 3.55- است که نشان میدهد به ازای افزایش هر سال سن خودرو قیمت آن 3.55 هزار یورو کاهش مییابد (شکل 1).

شکل 1. معادله خط رگرسیون
روش حداقل مربعات
روش حداقل مربعات شامل جستجو برای مقادیر بهینه عرض از مبدأ و شیب خط است تا بهترین خط ممکن از بین نقاط برازش یابد.
فرض کنید ما یک خط بطور تصادفی از بین نقاط عبور میدهیم. عرض از مبدأ این خط فرضی 25 و شیب آن 2 است (شکل 2). حالا سؤال این است که آیا این خط از خط قبلی بهتر است؟
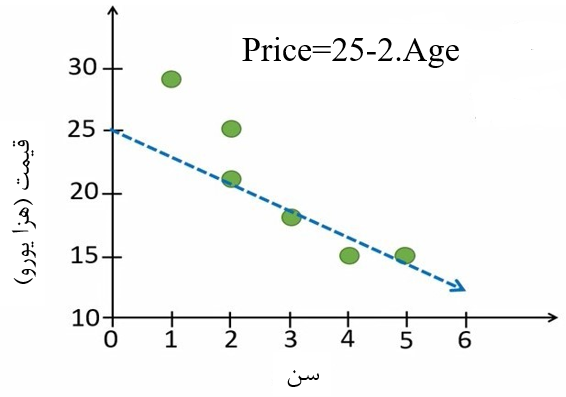
شکل 2. برازش یک خط تصادفی از بین نقاط
برای مقایسه این خط با خط قبلی از روش حداقل مربعات (Ordinary least square) استفاده میکنیم. در این روش مجموع مربعات تفاوت مشاهدات نسبت به خط باید کمترین مقدار را داشته باشد. برای فهم بهتر مطلب مثالی مطرح میکنیم.
مثال روش حداقل مربعات رگرسیون خطی
فرض کنید دو متغیر X و Y را اندازهگیری و نمودار پراکنش این دو متغیر را مانند شکل 3 رسم کردهایم.

شکل 3. اندازهگیری دو متغیر فرضی X و Y
حالا یک خط تصادفی بر دادهها برازش میکنیم. فرض کنید عرض از مبدأ این خط 3 و شیب آن 2 باشد (شکل 4).

شکل 4. برازش خط فرضی با عرض از مبدأ 3 و شیب 2
محل تقاطع خط با محور Y، عدد 3 را نشان میدهد که عرض از مبدأ است. خط فرضی ما شیب 2 دارد. یعنی به ازای افزایش یک واحد در X، مقدار Y دو واحد افزایش مییابد.
محاسبه حداقل مربعات خطا در رگرسیون
حداقل مربعات شامل فواصل عمودی نقاط از خط رگرسیون است. در رگرسیون خطی این فاصله اشتباه (Error) یا باقیمانده (Residual) نامیده میشود (شکل 5).
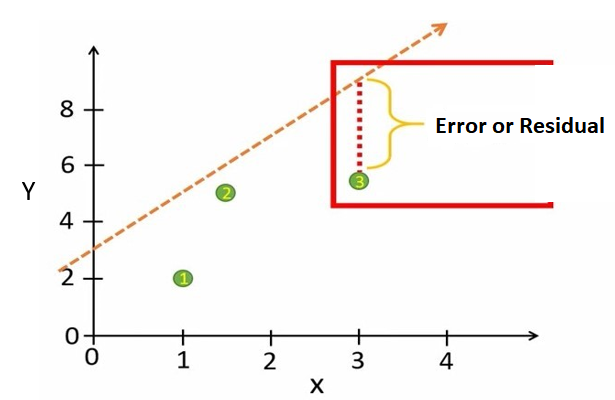
شکل 5. فاصله عمودی نقاط تا خط رگرسیون
اگر فاصله تمام نقاط نسبت خط رگرسیون را محاسبه، به توان دو برسانیم و با هم جمع کنیم، مجموع مربعات خطا (SSE) را بدست آوردهایم.
برای محاسبه فاصله بین نقاط و خط رگرسیون باید به ازای هر X مقداری تخمینی Y را بدست آوریم. اگر هر مقدار X را در معادله رگرسیون قرار دهیم و عملیات ریاضی انجام دهیم، مقداری تخمینی Y به ازای هر X بدست میآید.
مقادیر تخمینی Y به ازای هر X را در شکل 6 با Yest، نشان دادهایم.
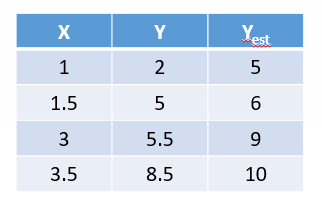
شکل 6. مقادیر تخمینی X به ازای هر Y
حالا میتوانیم فاصله عمودی نقاط را نسبت به خط محاسبه کنیم. اگر مقدار حقیقی Y را از مقدار تخمینی آن کسر کنیم، فاصله هر نقطه نسبت به خط رگرسیون بدست میآید (شکل 6).
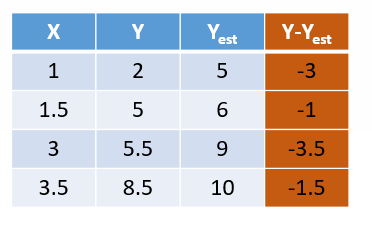
شکل 7. محاسبه فاصله نقاط نسبت به خط رگرسیون
در مرحله بعد باید فاصله نقاط نسبت به خط رگرسیون را به توان 2 برسانیم.
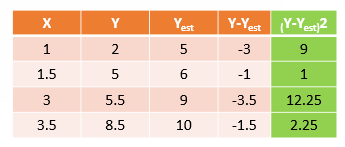
شکل 8. مربع فاصله نقاط نسبت به خط رگرسیون
حالا توان دوم اعداد را با هم جمع میکنیم تا مجموع مربعات بدست بیاید.

به این ترتیب مجموع مربعات خطا در خط ما با عرض از مبدأ 3 و شیب 2، عدد 24.5 بدست میآید.
الان میتوانیم خطوط دیگری را هم بطور تصادفی رسم کنیم و مجموع مربعات خطا را برای آن خطوط نیز محاسبه کنیم. در نهایت هر خطی که کمترین مجموع مربعات را داشته باشد، آن خط بهترین خط برای ما خواهد بود.
اما در عمل نیازی به این محاسبات برای بدست آوردن مقادیر بهینه شیب و عرض از مبدأ نیست.
محاسبه مقادیر بهینه شیب و عرض از مبدأ در رگرسیون خطی
برای محاسبه مقدار بهینه شیب و عرض از مبدأ میتوانیم از نرم افزارهای آماری کمک بگیریم. نرم افزارهای آماری مقدار عرض از مبدأ و شیب خط را در حالت حداقل مربعات خطا به ما میدهند.
البته برای رگرسیون خطی میتوانیم از فرمول زیر برای یافتن شیب خط رگرسیون استفاده کنیم.
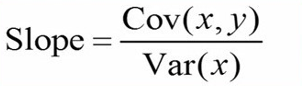
در صورت کسر این فرمول، کوواریانس X و Y و در مخرج کسر، واریانس X قرار میگیرد.
اگر عبارت کوواریانس و واریانس را در فرمول شیب خط قرار دهیم، فرمول شیب بصورت زیر در میآید:

با استفاده از فرمول بالا میتوانیم برای دادههای مثال، شیب خط را محاسبه کنیم. ابتدا میانگینهای X و Y را محاسبه میکنیم (شکل 9).
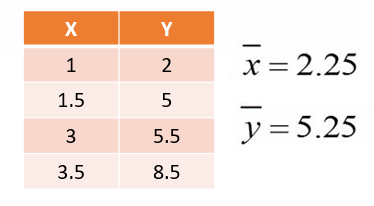
شکل 9. محاسبه میانگینهای X و Y
در نهایت با گذاشتن همه مقادیر در فرمول، شیب خط رگرسیون را محاسبه میکنیم:
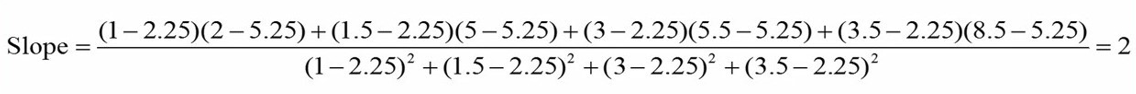
برای این مثال شیب خط را 2 بدست آوردیم.
عرض از مبدأ را نیز میتوانیم از طریق فرمول زیر محاسبه کنیم:
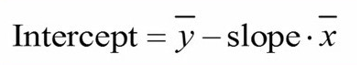
اگر میانگینهای X و Y و همچنین شیب خط را در فرمول جایگذاری کنیم، مقدار عرض از مبدأ بدست میآید:

پس معادله بهترین خطی که میتوانیم از بین دادهها عبور دهیم به شرح زیر است:


نظرات :