تحلیل عاملی تاییدی در آموس AMOS

تحلیل عاملی تاییدی برای روایی سازه‌های تحقیق استفاده می‌شود. در حقیقت تحلیل عاملی تاییدی زمانی مورد استفاده قرار می‌گیرد که بخواهیم ببینیم متغیرهای آشکار متغیر پنهانی مد نظر را اندازه‌گیری می کنند یا خیر؟ این تحلیل به سادگی در نرم افزار آموس AMOS قابل انجام است. توصیه می‌کنم مقالات زیر را نیز در مورد آموس نرم افزار آموس AMOS مطالعه نمایید.

• آشنایی با نرم افزار آموس AMOS
• تحلیل مسیر در نرم افزار آموس AMOS
• معادلات ساختاری در حالت نبود توزیع نرمال در آموس AMOS

مثال تحلیل عاملی تاییدی در آموس AMOS

به منظور انجام تحلیل عاملی تاییدی ابتدا مدل مورد نظر را در نرم افزار آموس AMOS رسم می‌کنیم. نحوه رسم مدل و استفاده از ابزارهای مختلف در آموس را قبلا در آموزش آشنایی با نرم افزار آموس فرا گرفته‌ایم.

مدل ما شامل سه متغیر پنهانی (anxiuos، dep و aff.lability) است که هر کدام توسط تعدادی متغیر آشکار اندازه‌گیری شده است. در این مدل اجازه‌ می دهیم که هر یک از فاکتورها با هم همبستگی داشته باشند. از این جهت یک فلش دو جهته بین هر کدام از عوامل رسم می ‌کنیم.

.

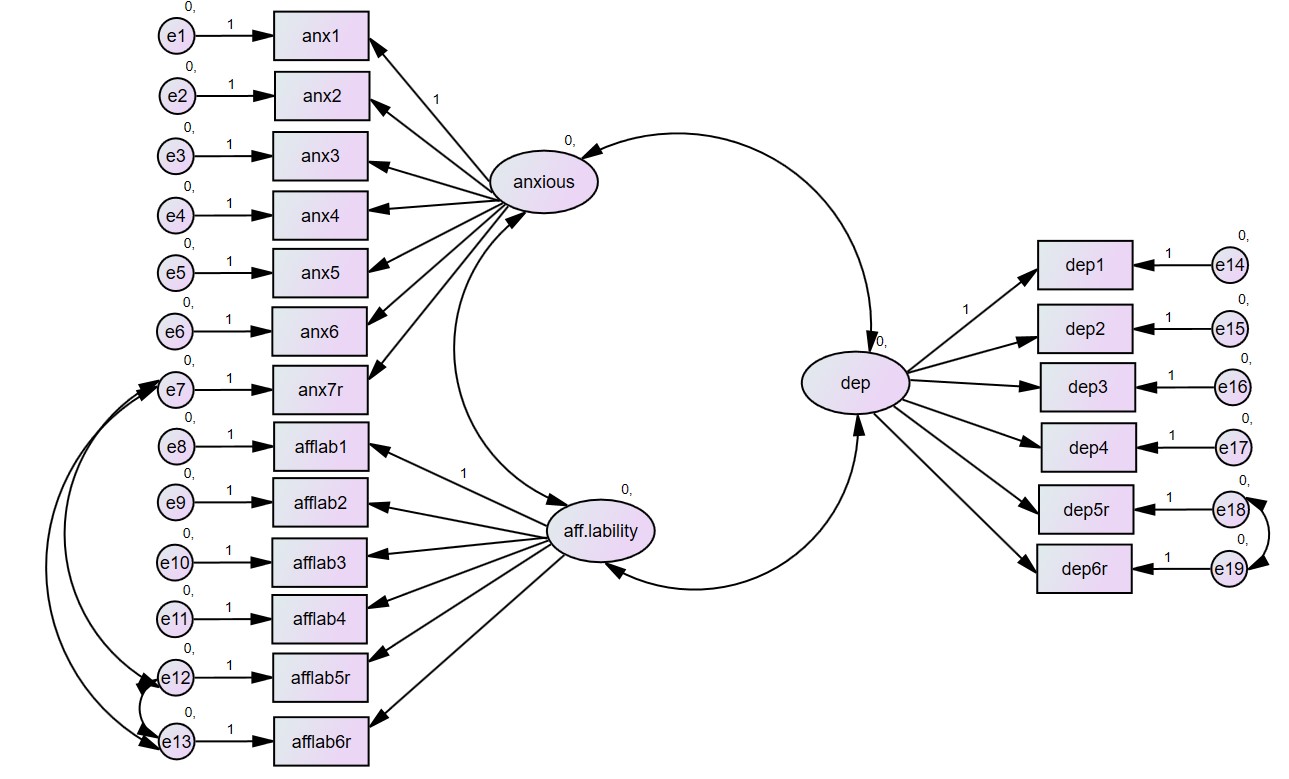
توضیح مدل برازش شده

اگر روی مدل دقت کنید، متوجه می‌شوید که یک مسیر از هر یک از متغیرهای پنهان به یک گویه یا نشانگر روی 1.0 ثابت است. این کار برای تعیین مقیاس اندازه گیری برای عامل پنهان انجام می‌شود. اگر عوامل پنهان شما دارای مقیاس اندازه گیری نباشد، مدل ناشناس خواهد بود  و اجرا نمی شود.  کار دیگری که می‌توانید انجام دهید این است که متغیرهای پنهان را استاندارد کنید تا میانگین 0 و انحراف معیار 1 داشته باشند. در این صورت، نیازی به تثبیت ضریب مسیر بر روی 1 نخواهد بود. به این منظور واریانس متغیرهای پنهان را روی 1 ثابت می‌کنیم.  بیشتر اوقات برای تغیین مقیاس اندازه‌گیری، محققان از استراتژی اول استفاده می‌کنند.

وجود داده‌های گم شده

اگر به هر دلیلی در تعدادی از متغیرهای شما داده گم شده وجود داشته باشد،  در این صورت تصمیم می‌گیریم که چگونه به این مشکل رسیدگی کنیم. یکی از گزینه‌ها این است که داده‌های خود را از همه مواردی که داده‌های از دست رفته روی متغیرهایتان وجود دارد پاک کنید و تجزیه و تحلیل را روی داده‌های باقیمانده  اجرا کنیم. گزینه دیگر استفاده از نوعی استراتژی برای جایگزین کردن نقاط داده است (به عنوان مثال، جایگزینی میانگین، برازش رگرسیون، برازش رگرسیون چندگانه) و اجرای تجزیه و تحلیل بر روی داده های جایگزین شده است.  گزینه دیگر استفاده از تخمین حداکثر درستنمایی برای تخمین میانگین‌ها و عرض از مبدآهاست. در AMOS، با کلیک بر روی گزینه “Estimate Means and Intercepts” در زیر تب “Estimation” در منو”Analysis Properties” این مورد فراخوانی می‌شود (شکل بالا).

توجه: اگر در مورد هر یک از متغیرهای در حال تجزیه و تحلیل، داده‌ای از دست رفته باشد و هنگام اجرای آنالیز خود در AMOS روی این گزینه کلیک نکنید، با پیام خطایی مواجه می‌شوید که از شما می‌خواهد هنگام اجرای برنامه خود، روی گزینه «Estimate means and intercepts» کلیک کنید.

تنظیمات اضافی مدل

در بخش «Analysis properties» می توانید گزینه های مختلفی را برای سفارشی سازی تحلیل مدل خود انتخاب کنید. من از قسمت «Output» دو گزینه «Standardized estimates» و «Squared multiple correlations» را فعال کردم (شکل بالا).
با کلیک بر روی «Standardized estimates»، بارهای عامل استاندارد شده بدست می‌آید. با کلیک بر روی «Squared multiple correlations»، مقادیر R-squared را بدست می‌آوریم.
زمانی که داده‌های گم شده داریم و تیک گزینه «Estimate means and intercepts» را فعال می‌کنیم در قسمت «Output»برخی از گزینه‌ها (به‌عنوان مثال، Residual moments، Tests for normality and outliers و  Modification indices) در دسترس نیستند.

بعد از انجام تنظیمات با کلیک بر دکمه «Calculate estimates» می‌توانیم پارامترهای مدل را برآورد کنیم.

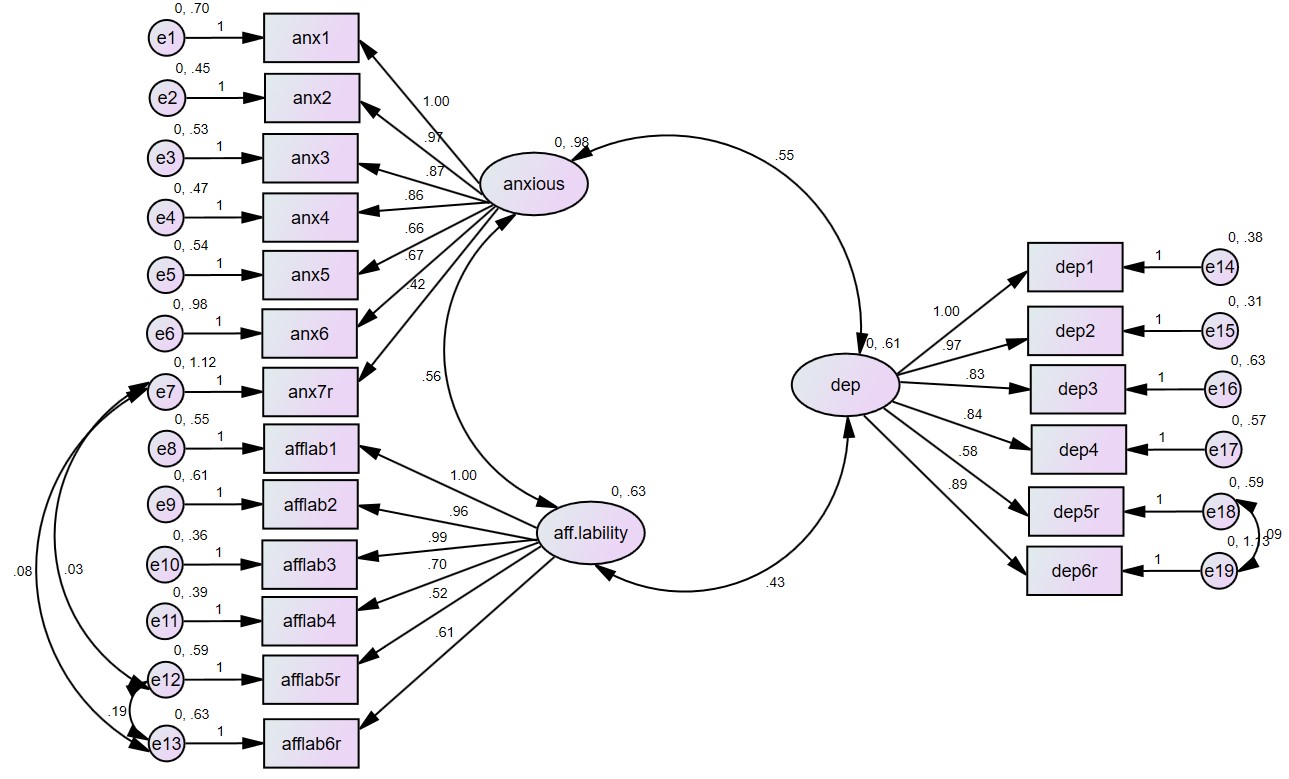
در شکل بالا می‌توانیم بارهای عاملی استاندارد نشده و همچنین واریانس متغیرهای پنهانی را روی شکل مشاهده کنیم.

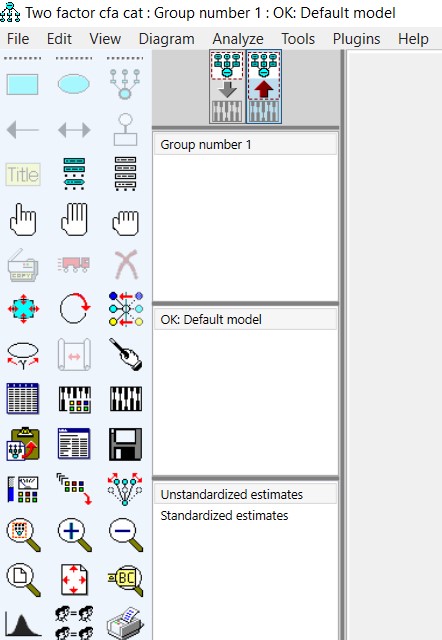
با کلیک بر گزینه «Standardized estimates» می‌توانیم ضرایب استاندارد شده را نیز ببینیم (شکل بالا).

بارهای استاندارد شده در مدل، در حقیقت همبستگی بین متغیرهای نشانگر (در مستطیل) و عوامل پنهان (بیضی) را نشان می‌دهد. فلش های دو سر بین عوامل پنهان (بیضی) نشان دهنده همبستگی است. فلش های دو سر بین عبارات خطا نشان دهنده همبستگی بین خطاها است.

برای مشاهده خروجی کامل، بر آیکون View Text کلیک می‌کنیم (شکل بالا).

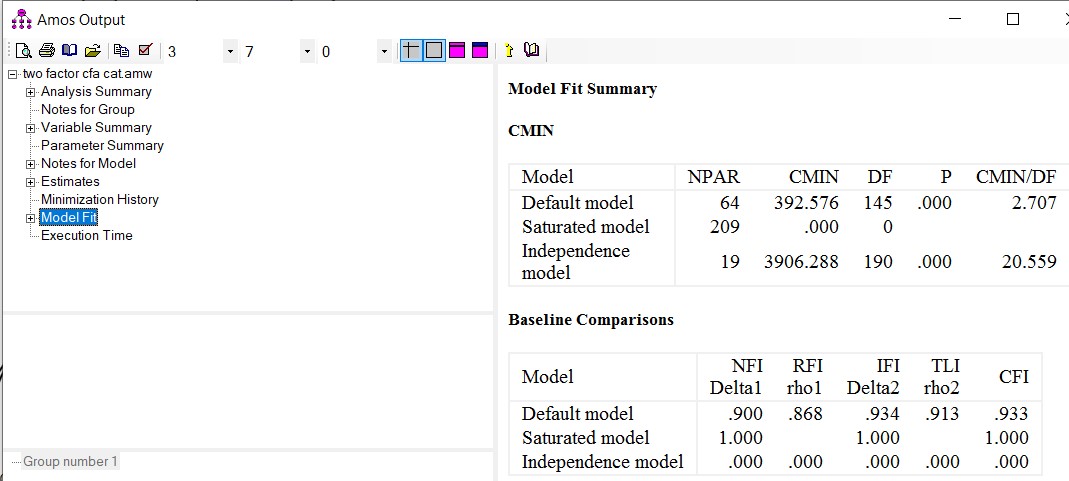
شاخص‌های برازش مدل (Model fit)

در خروجی نرم افزار ابتدا روی «Model Fit» کلیک می‌کنیم تا نیکویی برازش مدل را ببینیم. عبارت CMIN که در خروجی ظاهر می‌شود، مقادیر کای اسکوئر است. آزمون کای اسکوئر روشی برای ارزیابی برازش مدل است.  این آزمون  برای ارزیابی اینکه آیا مدل ما به طور معنی‌داری از مدلی که دقیقاً با داده‌ها مطابقت دارد فاصله می‌گیرد یا خیر استفاده می‌شود (Kline, 2016). عبارت  DF درجه آزادی آزمون کای اسکوئر است و P سطح معنی داری را نشان می‌دهد. عموماً، اگر p≤.05 باشد، فرض صفر را رد می‌کنیم و می‌گوییم مدل ما از مدلی که دقیقا بر داده‌ها مطابقت دارد فاصله دارد.

شاخص برازش هنجاردار (NFI)، شاخص برازش نسبی (RFI)، شاخص برازش افزایشی (IFI)، شاخص برازش مقایسه ای (CFI) و شاخص تاکر لوئیس (TLI؛ به عنوان شاخص برازش غیر هنجاردار یا NNFI نیز شناخته می‌شود) همگی شاخص‌های برازش افزایشی یا مقایسه‌ای هستند. یعنی به موجب آنها برازش یک مدل با مدل صفر یا مستقل مقایسه می‌شود (Byrne, 2010; Schumacker&Lomax, 2016). شاخص‌های  RFI، IFI، NNFI، و CFI همگی پیچیدگی‌های مدل را در محاسبات خود (به میزان بیشتر یا کمتر) به حساب می آورند. این شاخص ها معمولاً بین 0 و 1 متغیر هستند (اگرچه ممکن است مقادیر کمی بیشتر از 1 در برخی از آنها باشد). مقادیر بزرگتر از 0.9  برای این شاخص‌‌ها به عنوان مقادیر قابل قبول در نظر گرفته می‌شود (Whittaker, 2016). هر چند مقادیر بزرگتر از 0.95 نشان دهنده برازش مطلوب مدل می‌باشد (Byrne, 2010).

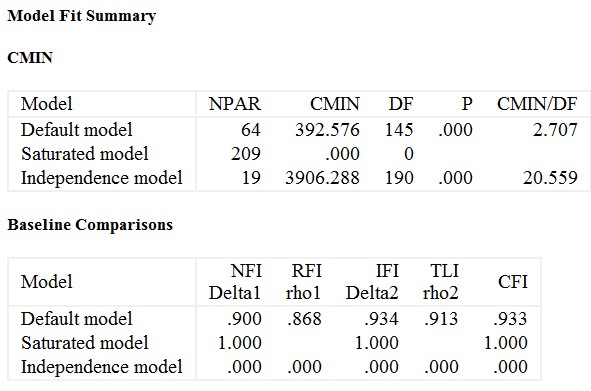
در مدل ما نتیجه آزمون کای دو نشان می‌دهد که مدل ما با یک مدلی که بر داده‌ها کاملا برازش دارد تفاوت معنی‌دار دارد (P<0.001).
شاخص‌های  TLI و CFI  بزرگتر از 0.9 هستند و با یک مدل قابل قبول سازگاری دارند.

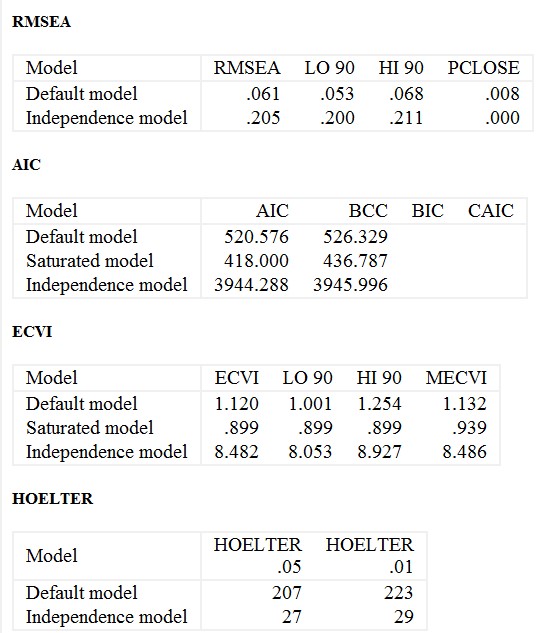
ریشه دوم میانگین مربعات خطای تخمین (RMSEA) را می توان یک “شاخص برازش مطلق” در نظر گرفت. در این شاخص عدد  0 نشان دهنده «بهترین تناسب» و مقادیر > 0 نشان دهنده برازش نامطلوب است (Kline، 2016). مقادیر 0.05 یا کمتر در RMSEA به طور کلی نشان دهنده یک مدل مطلوب در نظر گرفته می شود.
مقادیر بین 0.08 ( Brown & Cudeck، 1993) یا 0.10 (Hu & Bentler 1995) قابل قبول در نظر گرفته می شوند.  به گفته کلاین (Kline, 2016) مدل‌های با  RMSEA ≥ 0.10 از مشکل جدی در برازش رنج می‌برند.
در خروجی ما، RMSEA = 0.061 است که بین 0.05 (برازش مطلوب) و 0.10 (برازش ضعیف) قرار دارد. بنابراین RMSEA بر اساس مدل ما نشان می‌دهد که مدل ما برازش مطلوب با داده‌ها را نشان نمی‌دهد، اما برازش قابل قبول است. آزمون PCLOSE روش دیگری برای ارزیابی برازش یک مدل بر اساس RMSEA ارائه می دهد. اگر فرض کنیم که یک مقدار RMSEA ≤ 0.05 نشان دهنده یک مدل با برازش مطلوب باشد، آنگاه نتیجه آزمون p-close که در آن p> 0.05 باشد را می توان به عنوان تأییدیه دیگر مبنی بر برازش مطلوب در نظر گرفت (Kline, 2016). در تحلیل فعلی ما، PCLOSE 0.008 است، که رد فرضیه صفر برازش مطلوب  را نشان می‌دهد (یعنی مدل ما را پشتیبانی نمی‌کند).

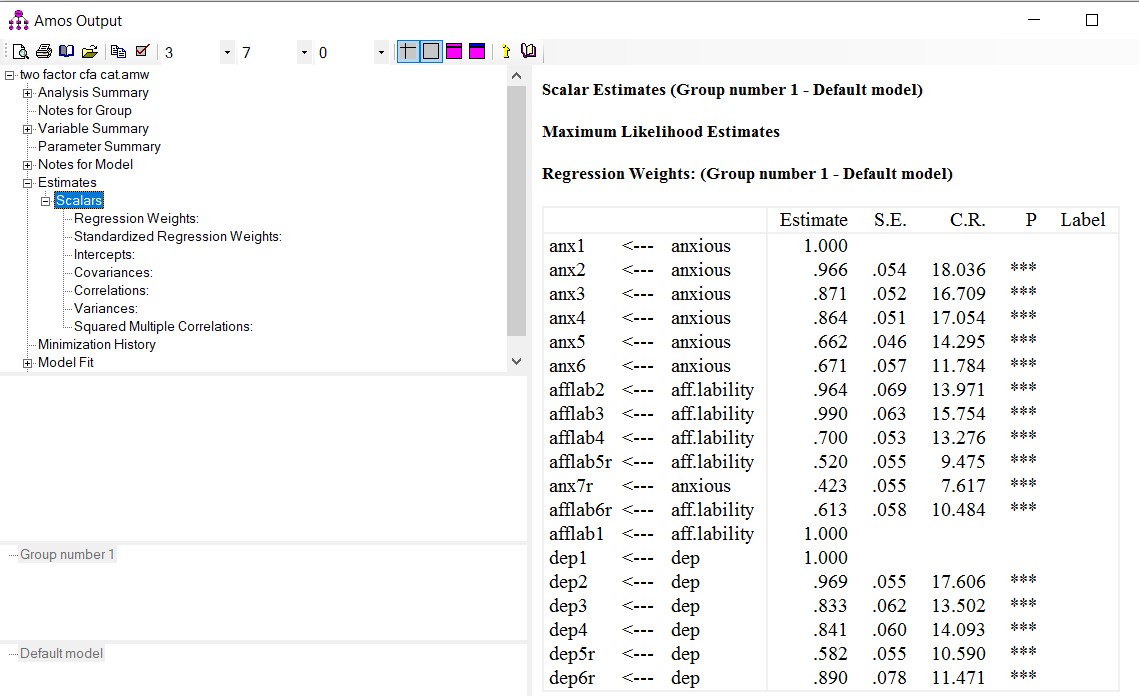
با کلیک بر روی “Estimates” و “Scalars” و “Regression Weights” بارهای عامل غیر استاندارد مشاهده می‌شود. بارهای عاملی که روی 1.0 ثابت شده‌اند شامل آزمون معناداری نمی‌شوند. در خروجی ما، همه بارهای عاملی مثبت و از نظر آماری معنی دار هستند.

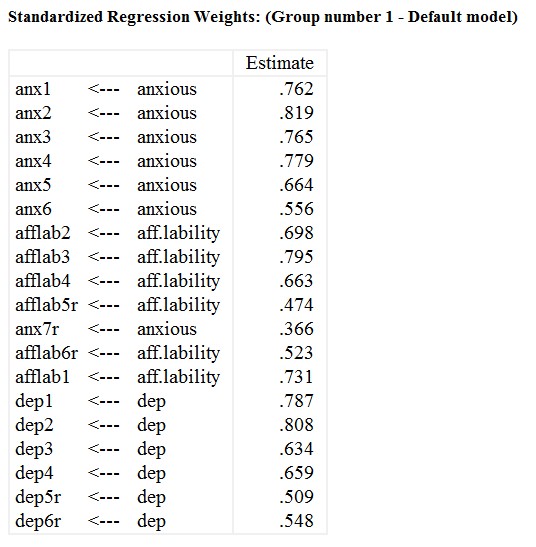
شکل بالا ضرایب مسیر استاندارد شده را نشان می‌دهد. از آنجایی که هر آیتم بر روی یک عامل بارگذاری می شود، بارهای عاملی به عنوان ضرایب همبستگی تفسیر می شوند. ما در اینجا می بینیم که همه بارهای عاملی به شدت مثبت هستند.

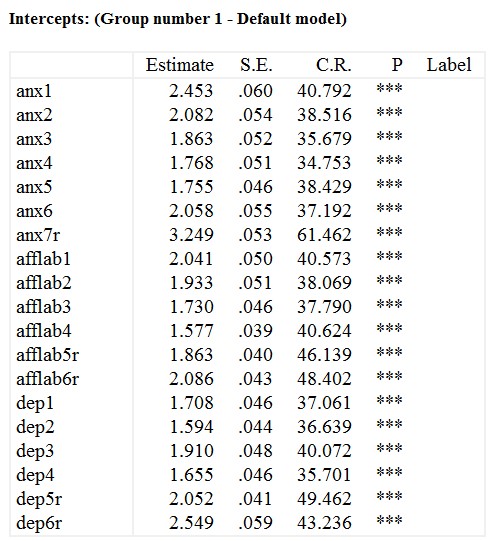
عرض از مبدأها (Intercepts) برای هر آیتم میانگین اصلاح شده آن آیتم بر مبنای ارتباط با عامل است.
جدول کوواریانس ها تخمینی از کوواریانس بین عوامل  و خطاهای اندازه گیری ارائه می دهد. مثلا همبستگی خطا بین آیتم 7 و آیتم 12 (0.428=p) و بین آیتم 7 و آیتم 13 (0.054=p) در سطح 0.05 غیرمعنادار است.

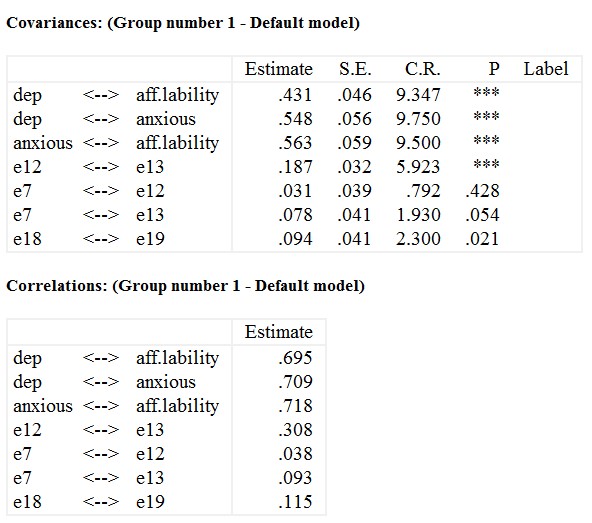
جدول بالا حاوی همبستگی بین عوامل و بین خطاهای است.

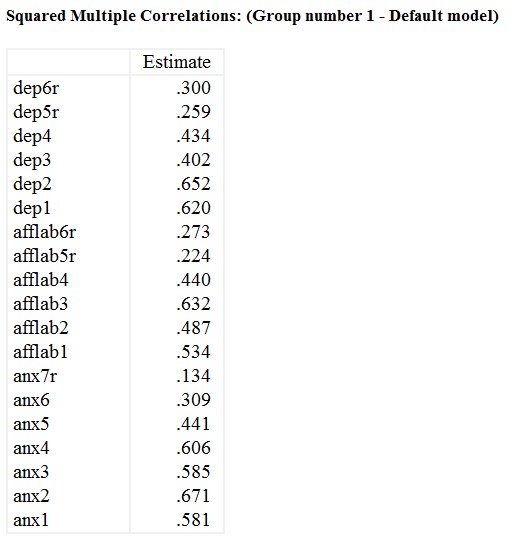
این جدول شامل مجذور همبستگی‌های چندگانه  است و می‌تواند مجموع آیتم‌های موجود در تجزیه و تحلیل ما را در نظر بگیرد. به طور خاص، ضرایب تبیین منعکس کننده نسبت تغییرات در توضیح داده‌ شده توسط عوامل نهفته هستند.
به عنوان مثال، عامل افسردگی 30٪ از تغییرات آیتم «dep6r» را توضیح می‌دهد. در حالی که عامل اضطراب تقریبا 60.6٪ از تغییرات را آیتم «anx4» را  توضیح می‌دهد.

T

References

Byrne, B. M. (2010). Structural equation modeling with AMOS: Basic concepts, applications, and programming (2^nd ed.). New York: Routledge.

International Personality Item Pool: A Scientific Collaboratory for the Development of Advanced Measures of Personality Traits and Other Individual Differences (http://ipip.ori.org/). Internet Web Site.

Kline, R. B. (2016). Principles and practice of structural equation modeling (4^th ed.). New York: The Guilford Press.

Lomax, R. G., & Hahs-Vaughn, D. L. (2012). An introduction to statistical concepts (3^rd ed.). New York: Routledge.

Pituch, K. A., & Stevens, J. P. (2016). Applied Multivariate Statistics for the Social Sciences (6^th ed.). New York: Routledge.

Schumacker, R. E., & Lomax, R. G. (2016). A beginner’s guide to structural equation modeling (4^th ed.). New York: Routledge.

Tabachnick, B. G., & Fidell, L. S. (2013). Using multivariate statistics (6^th edition). Pearson: Street, Upper Saddle River, New Jersey.

Whittaker, T. A. (2016). ‘Structural equation modeling’. Applied Multivariate Statistics for the Social Sciences (6^th ed.). Routledge: New York. 639-746.